Parte 14 : Prodotto Dot e Hadamard
Oltre alla moltiplicazione di matrice discussa prima, i vettori possono essere moltiplicati con altri due metodi: Prodotto a punti e prodotto di Hadamard. I risultati ottenuti da entrambi i metodi sono diversi.
Gli elementi corrispondenti alla stessa riga e colonna vengono moltiplicati insieme e i prodotti vengono aggiunti in modo che il risultato sia uno scalare.
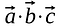
A differenza della moltiplicazione di matrici il risultato del prodotto a punti non è un altro vettore o matrice, è uno scalare.
L’ordine dei vettori non importa per il prodotto di punti, solo il numero di elementi in entrambi i vettori deve essere uguale.
La formula geometrica del prodotto di punti è
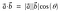
Il prodotto di punti è anche chiamato prodotto interno o prodotto scalare.
Proiezione del vettore
Assumendo che abbiamo due vettori c e d, sottesi dall’angolo, phi(Ф).
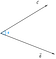
Ora, la proiezione del vettore c sul vettore d potrebbe essere rappresentata come
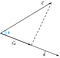
Si può concludere dalla figura che la proiezione è uguale alla componente orizzontale del vettore c rispetto all’angolo phi(Ф).
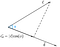
Questa si chiama proiezione scalare.Per trovare la proiezione vettoriale del vettore c sul vettore d dobbiamo moltiplicare la proiezione scalare con il vettore unitario d.
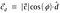
Sostituendo il valore del vettore unitario d.
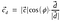
Quindi, il prodotto di punti potrebbe anche essere rappresentato come
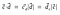
Le proiezioni sono ampiamente utilizzate in algebra lineare e nell’apprendimento automatico (Support Vector Machine(SVM) è un algoritmo di apprendimento automatico, utilizzato per la classificazione dei dati).
Prodotto di Hadamard (moltiplicazione per elementi)
Il prodotto di Hadamard di due vettori è molto simile all’addizione di matrici, gli elementi corrispondenti alle stesse righe e colonne di vettori/matrici dati sono moltiplicati insieme per formare un nuovo vettore/matrice.
Prende il nome dal matematico francese Jacques Hadamard.
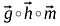
L’ordine delle matrici/vettori da moltiplicare deve essere lo stesso e anche la matrice risultante sarà dello stesso ordine.
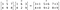

Il prodotto Hadamard è usato nelle tecniche di compressione delle immagini come JPEG. È anche conosciuto come prodotto Schur dal nome del matematico tedesco Issai Schur.
Il prodotto Hadamard è usato nelle celle LSTM (Long Short-Term Memory) delle reti neurali ricorrenti (RNN).
Leave a Reply