Matematica per le Arti Liberali
Risultati dell’apprendimento
- Definire e identificare l’autosimilarità in forme geometriche, piante, e formazioni geologiche
- Generare una forma frattale dato un iniziatore e un generatore
- Scalare un oggetto geometrico per un fattore di scala specifico usando la relazione di dimensione scalare
- Determinare la dimensione frattale di un oggetto frattale
Oltre all’autosimilarità visiva, i frattali mostrano altre proprietà interessanti. Per esempio, si noti che ogni passo dell’iterazione della guarnizione di Sierpinski rimuove un quarto dell’area rimanente. Se questo processo viene continuato all’infinito, finiremmo per rimuovere essenzialmente tutta l’area, il che significa che abbiamo iniziato con un’area bidimensionale, e in qualche modo ci ritroviamo con qualcosa di meno, ma apparentemente più di una linea unidimensionale.
Per esplorare questa idea, dobbiamo discutere la dimensione. Qualcosa come una linea è 1-dimensionale; ha solo la lunghezza. Qualsiasi curva è unidimensionale. Cose come scatole e cerchi sono bidimensionali, poiché hanno lunghezza e larghezza, descrivendo un’area. Oggetti come scatole e cilindri hanno lunghezza, larghezza e altezza, descrivendo un volume, e sono tridimensionali.
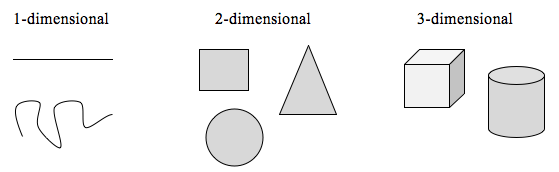
Si applicano alcune regole per scalare gli oggetti, relative alla loro dimensione.
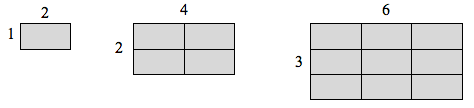
Se avessi una linea di lunghezza 1, e volessi scalare la sua lunghezza per 2, avrei bisogno di due copie della linea originale. Se avessi una linea di lunghezza 1, e volessi scalare la sua lunghezza di 3, avrei bisogno di tre copie dell’originale.
Se avessi un rettangolo di lunghezza 2 e altezza 1, e volessi scalare la sua lunghezza e larghezza di 2, avrei bisogno di quattro copie del rettangolo originale. Se volessi scalare la lunghezza e la larghezza per 3, avrei bisogno di nove copie del rettangolo originale.
Se avessi una scatola cubica con lati di lunghezza 1, e volessi scalare la sua lunghezza e larghezza di 2, avrei bisogno di otto copie del cubo originale. Se volessi scalare la lunghezza e la larghezza per 3, avrei bisogno di 27 copie del cubo originale.
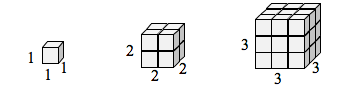
Nota che nel caso 1-dimensionale, le copie necessarie = scala.
Nel caso 2-dimensionale, le copie necessarie = scala^{2}.
Nel caso 3-dimensionale, le copie necessarie = scala^{3}.
Da questi esempi, potremmo dedurre uno schema.
Relazione scala-dimensione
Per scalare una forma D-dimensionale di un fattore di scala S, il numero di copie C della forma originale necessarie sarà dato da:
Testo{Copie}={Scala}^{Testo{Dimensione}}, o C=S^{D}
Esempio
Utilizzare la relazione scala-dimensione per determinare la dimensione della guarnizione di Sierpinski.
Supponiamo di definire che la guarnizione originale abbia il lato di lunghezza 1. La guarnizione più grande mostrata è due volte più larga e due volte più alta, quindi è stata scalata di un fattore 2.
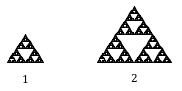
Nota che per costruire la guarnizione più grande, sono necessarie 3 copie della guarnizione originale.
Utilizzando la relazione scala-dimensione C=S^{D}, otteniamo l’equazione 3=2^{D}.
Siccome 2^{1}=2 e 2^{2}=4, possiamo immediatamente vedere che D è da qualche parte tra 1 e 2; la guarnizione è più di una forma a 1 dimensione, ma abbiamo tolto così tanta area che ora è meno di 2 dimensioni.
La soluzione dell’equazione 3=2^{D} richiede logaritmi. Se avete studiato i logaritmi in precedenza, potreste ricordare come risolvere questa equazione (se no, passate al riquadro sottostante e usate la formula con il tasto log su una calcolatrice):
Prendete il logaritmo di entrambi i lati.
3={{2}^{D}}
Utilizzate la proprietà degli esponenti dei log.
\log(3)=\log\sinistra({{2}^{D}}}destra)
Dividere per log(2).
Log(3)=Dlog\left(2\destra)
La dimensione della guarnizione è circa 1,585.
D=frac{log\left(3\destra)}{\log(2)}approx1.585
Relazione scala-dimensione, per trovare la dimensione
Per trovare la dimensione D di un frattale, determinare il fattore di scala S e il numero di copie C della forma originale necessarie, poi usa la formula
D=frac{\log\sinistra(C\destra)}{log(S)}
Prova
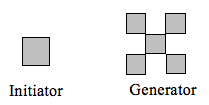
Determina la dimensione frattale del frattale prodotto usando l’iniziatore e il generatore.
Nel seguente video, presentiamo un esempio lavorato di come determinare la dimensione della guarnizione di Sierpinski

Leave a Reply