Introduzione alla deconvoluzione

La deconvoluzione è una tecnica di elaborazione delle immagini ad alta intensità di calcolo che viene sempre più utilizzata per migliorare il contrasto e la risoluzione delle immagini digitali catturate al microscopio. Le basi si basano su una serie di metodi che sono progettati per rimuovere o invertire la sfocatura presente nelle immagini del microscopio indotta dall’apertura limitata dell’obiettivo.

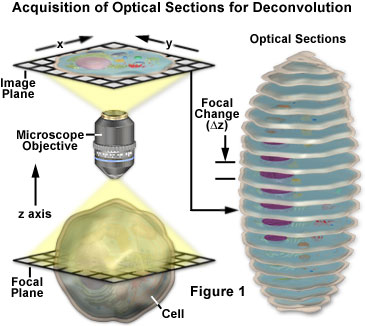
Quasi qualsiasi immagine acquisita su un microscopio a fluorescenza digitale può essere deconvolta, e diverse nuove applicazioni sono state sviluppate che applicano tecniche di deconvoluzione a immagini in luce trasmessa raccolte sotto una varietà di strategie di miglioramento del contrasto. Tra i soggetti più adatti al miglioramento tramite deconvoluzione ci sono i montaggi tridimensionali costruiti da una serie di sezioni ottiche.

I concetti di base che circondano l’acquisizione di immagini in serie z per l’analisi di deconvoluzione sono presentati con un diagramma schematico nella Figura 1. Viene registrata una serie di immagini del campione, ognuna leggermente spostata l’una dall’altra lungo l’asse z. Questo cambiamento nel piano focale si traduce in un’immagine leggermente diversa, con sottili cambiamenti causati dalla luce fuori fuoco proveniente da sopra e sotto il piano z corrente. Durante l’analisi di deconvoluzione, l’intera serie z viene analizzata per creare un set di dati più chiaro e di più alta risoluzione che non è convoluto dalla fluorescenza fuori fuoco.

Deconvoluzione è spesso suggerito come una buona alternativa al microscopio confocale, come entrambe le tecniche cercano di ridurre al minimo l’effetto della fluorescenza fuori fuoco sulla vostra immagine finale. Questo non è strettamente vero perché le immagini acquisite utilizzando un foro stenopeico in un microscopio confocale beneficiano dell’elaborazione della deconvoluzione. La microscopia confocale impedisce alla luce fuori fuoco di essere rilevata ponendo un foro stenopeico tra l’obiettivo e il rivelatore, attraverso il quale possono passare solo i raggi di luce a fuoco. Al contrario, i microscopi ad ampio campo permettono alla luce fuori fuoco di passare direttamente al rivelatore. La deconvoluzione viene poi applicata alle immagini risultanti per sottrarre la luce fuori fuoco o riassegnarla alla sua fonte. La microscopia confocale è particolarmente adatta per l’esame di campioni spessi come gli embrioni o le cozze, mentre l’elaborazione della deconvoluzione a largo campo ha dimostrato di essere uno strumento potente per l’imaging di campioni che richiedono livelli di luce estremamente bassi. Questi strumenti possono anche essere combinati per ridurre il rumore nelle immagini acquisite su un microscopio confocale. Tuttavia, la maggior parte degli esperimenti di deconvoluzione riportati in letteratura si applicano a immagini registrate su un microscopio a fluorescenza standard a largo campo.

Fonti di degrado dell’immagine

Il degrado dell’immagine può essere diviso in quattro fonti indipendenti: rumore, dispersione, riflesso e sfocatura. La figura 2 presenta esempi dell’impatto visivo di ognuna di esse sulla stessa immagine.

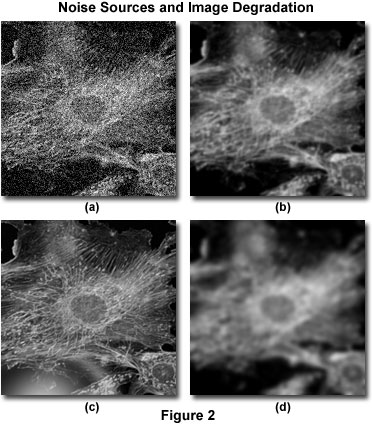
Il rumore può essere descritto come una disorganizzazione quasi casuale dei dettagli in un’immagine, che (nella sua forma più grave) ha l’aspetto di rumore bianco o rumore sale e pepe, simile a quello che si vede in televisione quando si ha cattiva ricezione (Figura 2(a)). Questo tipo di rumore viene definito “quasi-casuale” perché la distribuzione statistica può essere prevista se si conosce la meccanica della sorgente. Nella microscopia digitale, la principale fonte di rumore è il segnale stesso (spesso indicato come rumore da colpo di fotone) o il sistema di imaging digitale. La meccanica di entrambe le fonti di rumore è compresa e quindi la distribuzione statistica del rumore è nota. Il rumore dipendente dal segnale può essere caratterizzato da una distribuzione di Poisson, mentre il rumore derivante dal sistema di imaging segue spesso una distribuzione gaussiana. Poiché la fonte e la distribuzione del rumore comune nelle immagini digitali è così ben compresa, può essere facilmente rimosso applicando i filtri immagine appropriati, che sono di solito inclusi nella maggior parte dei pacchetti software di deconvoluzione come una routine opzionale di “pre-elaborazione”.

Lo scatter è di solito indicato come un disturbo casuale della luce indotto dai cambiamenti di indice di rifrazione in un campione. L’effetto netto della dispersione è una disorganizzazione veramente casuale dei dettagli dell’immagine, come si manifesta nella Figura 2(b). Sebbene non sia stato sviluppato un metodo completamente soddisfacente per prevedere la dispersione in un dato campione, è stato dimostrato che il grado di dispersione dipende fortemente dallo spessore del campione e dalle proprietà ottiche del campione e dei materiali circostanti. La dispersione aumenta sia con lo spessore del campione che con l’eterogeneità dell’indice di rifrazione presentato dai componenti interni di un campione.

Simile alla dispersione, il bagliore è un disturbo casuale della luce, ma si verifica negli elementi ottici (lenti, filtri, prismi, ecc.) del microscopio piuttosto che nel campione. Il livello di abbagliamento in un microscopio moderno è stato minimizzato dall’impiego di lenti e filtri con rivestimenti antiriflesso, e dal perfezionamento delle tecniche di formatura delle lenti, dei cementi ottici e delle formulazioni del vetro. La figura 2(c) illustra l’effetto del bagliore incontrollato.

La sfocatura è descritta da una diffusione non casuale della luce che si verifica al passaggio attraverso il percorso ottico del sistema di imaging (figura 2(d)). La fonte più significativa di sfocatura è la diffrazione, e un’immagine la cui risoluzione è limitata solo dalla sfocatura è considerata limitata dalla diffrazione. Questo rappresenta un limite intrinseco di qualsiasi sistema di imaging ed è il fattore determinante nella valutazione del limite di risoluzione di un sistema ottico. Fortunatamente, sono disponibili modelli sofisticati di sfocatura in un microscopio ottico che possono essere utilizzati per determinare la fonte dei fotoni fuori fuoco. Questa è la base della deconvoluzione. A causa della sua importanza fondamentale nella deconvoluzione, il modello teorico della sfocatura sarà discusso molto più dettagliatamente in altre parti di questa sezione. Tuttavia, si dovrebbe sottolineare che tutti i sistemi di imaging producono sfocatura indipendentemente dalle altre forme di degradazione dell’immagine indotte dal campione o dall’elettronica strumentale di accompagnamento. È proprio questa indipendenza della sfocatura ottica da altri tipi di degradazione che permette la possibilità di rimozione della sfocatura con tecniche di deconvoluzione.

L’interazione della luce con la materia è l’origine fisica primaria della dispersione, del bagliore e della sfocatura. Tuttavia, la composizione e la disposizione delle molecole in un dato materiale (sia esso vetro, acqua o proteine) conferisce a ciascun materiale il suo particolare insieme di proprietà ottiche. Ai fini della deconvoluzione, ciò che distingue la dispersione, l’abbagliamento e la sfocatura sono la posizione in cui si verificano e la possibilità di generare un modello matematico per questi fenomeni. Poiché lo scatter è un fenomeno localizzato e irregolare che si verifica nel campione, si è dimostrato difficile da modellare. Al contrario, poiché la sfocatura è una funzione del sistema ottico del microscopio (principalmente l’obiettivo), può essere modellata con relativa semplicità. Un tale modello rende possibile invertire matematicamente il processo di sfocatura, e la deconvoluzione impiega questo modello per invertire o rimuovere la sfocatura.

La funzione di diffusione del punto

Il modello di sfocatura che si è sviluppato nell’ottica teorica si basa sul concetto di una funzione di diffusione del punto tridimensionale (PSF). Questo concetto è di fondamentale importanza per la deconvoluzione e dovrebbe essere chiaramente compreso al fine di evitare artefatti di imaging. La funzione di diffusione del punto si basa su una sorgente di luce puntiforme infinitamente piccola che ha origine nello spazio del campione (oggetto). Poiché il sistema di imaging del microscopio raccoglie solo una frazione della luce emessa da questo punto, non può mettere a fuoco la luce in una perfetta immagine tridimensionale del punto. Invece, il punto appare allargato e diffuso in un modello di diffrazione tridimensionale. Così, la funzione di diffusione del punto è formalmente definita come il modello di diffrazione tridimensionale generato da una sorgente puntiforme di luce ideale.

A seconda della modalità di imaging utilizzata (campo largo, confocale, luce trasmessa), la funzione di diffusione del punto ha una forma e un contorno diversi e unici. In un microscopio a fluorescenza ad ampio campo, la forma della funzione di diffusione del punto assomiglia a quella di un “calcio” oblungo di luce circondato da un bagliore di anelli che si allargano. Per descrivere la funzione di diffusione del punto in tre dimensioni, è comune applicare un sistema di coordinate di tre assi (x, y e z) dove × e y sono paralleli al piano focale del campione e z è parallelo all’asse ottico del microscopio. In questo caso, la funzione di diffusione del punto appare come un insieme di anelli concentrici nel piano x-y, e assomiglia a una clessidra nei piani x-z e y-z (come illustrato nella Figura 3). Una fetta x-y attraverso il centro della funzione di diffusione del punto ad ampio campo rivela un insieme di anelli concentrici: il cosiddetto disco di Airy che è comunemente citato nei testi sulla microscopia ottica classica.

Due proiezioni x-z di funzioni di diffusione del punto che mostrano diversi gradi di aberrazione sferica sono presentati nella Figura 3. L’asse ottico è parallelo all’asse verticale dell’immagine. La funzione di diffusione del punto a sinistra mostra un’aberrazione sferica minima, mentre quella a destra mostra un grado significativo di aberrazione. Si noti che l’asimmetria assiale e l’allargamento del nodo centrale lungo l’asse ottico nell’immagine di destra porta a una risoluzione assiale degradata e alla sfocatura del segnale. In teoria, la dimensione della funzione di diffusione del punto è infinita, e l’intensità totale sommata della luce nei piani lontani dal fuoco è uguale all’intensità sommata a fuoco. Tuttavia, l’intensità della luce diminuisce rapidamente e alla fine diventa indistinguibile dal rumore. In una funzione di diffusione puntiforme non aberrata registrata con un obiettivo a immersione in olio ad alta apertura numerica (1,40), la luce che occupa 0,2 micrometri quadrati sul piano di messa a fuoco è diffusa su 90 volte quell’area a 1 micrometro sopra e sotto il fuoco. Il campione utilizzato per registrare queste immagini della funzione di diffusione del punto era una perlina fluorescente di 0,1 micrometri di diametro montata in glicerolo (indice di rifrazione uguale a 1,47), con oli di immersione aventi gli indici di rifrazione indicati nella figura.

Un’importante considerazione è come la funzione di diffusione del punto influisce sulla formazione dell’immagine nel microscopio. Il modello teorico della formazione dell’immagine tratta la funzione di diffusione del punto come l’unità di base di un’immagine. In altre parole, la funzione di diffusione del punto è per l’immagine ciò che il mattone è per la casa. Il meglio che un’immagine possa mai essere è un assemblaggio di funzioni di diffusione del punto, e aumentare l’ingrandimento non cambierà questo fatto. Come spiega un noto libro di testo di ottica teorica (Born e Wolf: Principles of Optics), “È impossibile far emergere dettagli non presenti nell’immagine primaria aumentando la potenza dell’oculare, perché ogni elemento dell’immagine primaria è un piccolo modello di diffrazione, e l’immagine reale, vista dall’oculare, è solo l’insieme delle immagini ingrandite di questi modelli”.

Come esempio, consideriamo una popolazione di perline fluorescenti a sub-risoluzione inserita tra un coprioggetto e un vetrino da microscopio. Un’immagine a fuoco di questo campione rivela una nuvola di punti, che è in realtà un disco circondato da un piccolo insieme di anelli (in effetti, un disco di Airy; vedi Figura 4(a)). Se questo campione viene leggermente rimosso dalla messa a fuoco, una serie più grande di anelli concentrici apparirà dove ogni punto era nell’immagine focalizzata (Figura 4(b)). Quando viene raccolta un’immagine tridimensionale di questo campione, viene registrata una funzione di diffusione del punto completa per ogni perlina. La funzione di diffusione del punto descrive cosa succede ad ogni sorgente puntiforme di luce dopo che passa attraverso il sistema di imaging.

Il processo di sfocatura appena descritto è modellato matematicamente come una convoluzione. L’operazione di convoluzione descrive l’applicazione della funzione di diffusione del punto ad ogni punto del campione: la luce emessa da ogni punto dell’oggetto è convoluta con la funzione di diffusione del punto per produrre l’immagine finale. Sfortunatamente, questa convoluzione fa sì che i punti del campione diventino regioni sfocate nell’immagine. La luminosità di ogni punto dell’immagine è correlata linearmente dall’operazione di convoluzione alla fluorescenza di ogni punto del campione. Poiché la funzione di diffusione del punto è tridimensionale, la sfocatura dalla funzione di diffusione del punto è un fenomeno intrinsecamente tridimensionale. L’immagine da qualsiasi piano focale contiene luce sfocata da punti situati in quel piano mescolata con luce sfocata da punti originati in altri piani focali.

La situazione può essere riassunta con l’idea che l’immagine è formata da una convoluzione del campione con la funzione di diffusione del punto. La deconvoluzione inverte questo processo e tenta di ricostruire il campione da un’immagine sfocata.

Aberrazioni nella funzione di diffusione del punto

La funzione di diffusione del punto può essere definita sia teoricamente utilizzando un modello matematico di diffrazione, o empiricamente acquisendo un’immagine tridimensionale di una perlina fluorescente (vedi Figura 3). Una funzione di diffusione teorica ha generalmente una simmetria assiale e radiale. In effetti, la funzione di diffusione del punto è simmetrica sopra e sotto il piano x-y (simmetria assiale) e in rotazione attorno all’asse z (simmetria radiale). Una funzione di diffusione del punto empirica può deviare significativamente dalla simmetria perfetta (come presentato nella Figura 3). Questa deviazione, più comunemente chiamata aberrazione, è prodotta da irregolarità o disallineamenti in qualsiasi componente del treno ottico del sistema di imaging, in particolare l’obiettivo, ma può anche verificarsi con altri componenti come specchi, beamsplitters, lenti del tubo, filtri, diaframmi e aperture. Più alta è la qualità dei componenti ottici e migliore è l’allineamento del microscopio, più la funzione di diffusione dei punti empirici si avvicina alla sua forma simmetrica ideale. Sia la microscopia confocale che quella con deconvoluzione dipendono dal fatto che la funzione di diffusione dei punti sia il più vicino possibile al caso ideale.

L’aberrazione più comune che si incontra nella microscopia ottica, ben nota a qualsiasi microscopista esperto e professionale, è l’aberrazione sferica. La manifestazione di questa aberrazione è un’asimmetria assiale nella forma della funzione di diffusione del punto, con un corrispondente aumento delle dimensioni, in particolare lungo l’asse z (Figura 3). Il risultato è una notevole perdita di risoluzione e di intensità del segnale. In pratica, la tipica fonte di aberrazione sferica è una discrepanza tra gli indici di rifrazione del mezzo di immersione della lente frontale dell’obiettivo e il mezzo di montaggio in cui è immerso il campione. Si dovrebbe porre un’enorme enfasi sull’importanza di ridurre al minimo questa aberrazione. Anche se la deconvoluzione può ripristinare parzialmente la risoluzione persa, nessuna quantità di elaborazione dell’immagine può ripristinare il segnale perso.