Introduzione al Consistent Hashing

Con l’aumento delle architetture distribuite, il consistent hashing è diventato mainstream. Ma cos’è esattamente e come è diverso da un algoritmo di hashing standard? Quali sono le esatte motivazioni dietro?

Prima di tutto, descriveremo i concetti principali. Poi, scaveremo negli algoritmi esistenti per capire le sfide associate all’hashing coerente.

Hashing

Hashing è il processo per mappare dati di dimensione arbitraria in valori di dimensione fissa. Ogni algoritmo esistente ha le sue specifiche:

• MD5 produce valori di hash a 128 bit.
• SHA-1 produce valori di hash a 160 bit.
• ecc.

Hashing ha molte applicazioni in informatica. Per esempio, una di queste applicazioni è chiamata checksum. Per verificare l’integrità di un set di dati è possibile utilizzare un algoritmo di hashing. Un server esegue l’hash di un set di dati e indica il valore di hash a un client. Poi, il client esegue l’hash della sua versione del set di dati e confronta i valori di hash. Se sono uguali, l’integrità dovrebbe essere verificata.

Il “dovrebbe” qui è importante. Lo scenario peggiore è quando si verifica una collisione. Una collisione è quando due pezzi distinti di dati hanno lo stesso valore di hash. Facciamo un esempio di vita reale definendo la seguente funzione di hashing: data una persona restituisce la data del suo compleanno (giorno & mese di nascita). Il paradosso del compleanno ci dice che se abbiamo solo 23 persone in una stanza, la probabilità che due persone abbiano lo stesso compleanno (quindi una collisione) è più del 50%. Pertanto, la funzione di compleanno non è probabilmente una buona funzione di hashing.

Come introduzione veloce all’hashing è importante capire che l’idea principale riguarda la diffusione di valori in un dominio. Per esempio:

• MD5 distribuisce i valori su un dominio di spazio di 128 bit
• Un hashtable (o hashmap) sostenuto da un array di 32 elementi ha una funzione di hashing interna che distribuisce i valori su qualsiasi indice (da 0 a 31).

Distribuzione del carico

La distribuzione del carico può essere definita come il processo di distribuzione del carico sui nodi. Il termine nodo qui è intercambiabile con server o istanza. È un’unità di calcolo.

Il bilanciamento del carico è un esempio di distribuzione del carico. Si tratta di distribuire un insieme di compiti su un insieme di risorse. Per esempio, usiamo il bilanciamento del carico per distribuire le richieste API tra le istanze del server web.

Quando si tratta di dati, usiamo piuttosto il termine sharding. Uno shard di database è una partizione orizzontale di dati in un database. Un esempio tipico è un database partizionato in tre shard dove ogni shard ha un sottoinsieme dei dati totali.

Il bilanciamento del carico e lo sharding condividono alcune sfide comuni. Distribuire i dati in modo uniforme, per esempio, per garantire che un nodo non sia sovraccaricato rispetto agli altri. In alcuni contesti, il bilanciamento del carico e lo sharding hanno anche bisogno di continuare ad associare compiti o dati allo stesso nodo:

• Se abbiamo bisogno di serializzare, gestire una per una, le operazioni per un dato consumatore, dobbiamo instradare la richiesta allo stesso nodo.
• Se abbiamo bisogno di distribuire dati, dobbiamo sapere quale shard è il proprietario per una particolare chiave.

Ti suona familiare? In questi due esempi, abbiamo distribuito valori in un dominio. Che si tratti di un compito distribuito ai nodi del server o di dati distribuiti allo shard del database, ritroviamo l’idea associata all’hashing. Questo è il motivo per cui l’hashing può essere usato insieme alla distribuzione del carico. Vediamo come.

Mod-n Hashing

Il principio del mod-n hashing è il seguente. Ogni chiave è sottoposta a hashing usando una funzione di hashing per trasformare un input in un intero. Poi, si esegue un modulo basato sul numero di nodi.

Vediamo un esempio concreto con 3 nodi. Qui, abbiamo bisogno di distribuire il carico tra questi nodi sulla base di un identificatore di chiave. Ogni chiave è sottoposta a hash, poi eseguiamo un’operazione modulo:

Il vantaggio di questo approccio è la sua assenza di stato. Non dobbiamo mantenere nessuno stato per ricordarci che foo è stato instradato al nodo 2. Tuttavia, abbiamo bisogno di sapere quanti nodi sono configurati per applicare l’operazione modulo.

Poi, come funziona il meccanismo in caso di scaling out o in (aggiunta o rimozione di nodi)? Se aggiungiamo un altro nodo, l’operazione modulo è ora basata su 4 invece di 3:

Come possiamo vedere, le chiavi foo e baz non sono più associate allo stesso nodo. Con il mod-n hashing, non c’è alcuna garanzia di mantenere la coerenza nell’associazione chiave/nodo. È un problema? Potrebbe.

Che cosa succede se implementiamo un datastore usando lo sharding e basandoci sulla strategia mod-n per distribuire i dati? Se scaliamo il numero di nodi, dobbiamo eseguire un’operazione di riequilibrio. Nell’esempio precedente, riequilibrare significa:

• Spostamento di foo dal nodo 2 al nodo 0.
• Spostamento di baz dal nodo 2 al nodo 3.

Ora, cosa succede se abbiamo memorizzato milioni o addirittura miliardi di dati e dobbiamo riequilibrare quasi tutto? Come possiamo immaginare, questo sarebbe un processo pesante. Pertanto, dobbiamo cambiare la nostra tecnica di distribuzione del carico per assicurarci che al momento del riequilibrio:

• La distribuzione rimanga il più uniforme possibile in base al nuovo numero di nodi.
• Il numero di chiavi che dobbiamo migrare dovrebbe essere limitato. Idealmente, sarebbe solo 1/n per cento delle chiavi dove n è il numero di nodi.

Questo è esattamente lo scopo degli algoritmi di hashing coerenti.

Il termine coerente potrebbe però confondere un po’. Ho incontrato ingegneri che supponevano che tali algoritmi continuassero ad associare una data chiave allo stesso nodo anche di fronte alla scalabilità. Questo non è il caso. Deve essere coerente fino ad un certo punto per mantenere la distribuzione uniforme.

Ora, è il momento di scavare in alcune soluzioni.

Rendezvous

Rendezvous è stato il primo algoritmo mai proposto per risolvere il nostro problema. Anche se lo studio originale, pubblicato nel 1996, non menziona il termine consistent hashing, fornisce una soluzione alle sfide che abbiamo descritto. Vediamo una possibile implementazione in Go:

Come funziona? Attraversiamo ogni nodo e calcoliamo il suo valore di hash. Il valore di hash è restituito da una funzione hashche produce un intero basato su una chiave (il nostro input) e un identificatore di nodo (l’approccio più semplice è quello di hashare la concatenazione delle due stringhe). Poi, restituiamo il nodo con il più alto valore di hash. Questo è il motivo per cui l’algoritmo è anche conosciuto come hashing a peso casuale più alto.

Il principale svantaggio di rendezvous è la sua complessità temporale O(n) dove n è il numero di nodi. È molto efficiente se abbiamo bisogno di avere un numero limitato di nodi. Tuttavia, se iniziamo a mantenere migliaia di nodi, potrebbe iniziare a causare problemi di prestazioni.

Ring Consistent Hash

L’algoritmo successivo è stato rilasciato nel 1997 da Karger et al. Questo studio ha menzionato per la prima volta il termine hashing coerente.

Si basa su un anello (un array connesso end-to-end). Sebbene sia l’algoritmo di hashing coerente più popolare (o almeno il più conosciuto), il principio non è sempre ben compreso. Immergiamoci in esso.

La prima operazione è quella di creare l’anello. Un anello ha una lunghezza fissa. Nel nostro esempio, lo dividiamo in 12 parti:

Poi, posizioniamo i nostri nodi. Nel nostro esempio definiremo N0, N1 e N2.

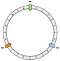
I nodi sono distribuiti uniformemente per il momento. Torneremo su questo punto più tardi.

Poi, è il momento di vedere come rappresentare le chiavi. Per prima cosa, abbiamo bisogno di una funzione f che restituisca un indice ad anello (da 0 a 11) basato su una chiave. Possiamo usare il mod-n hashing per questo. Poiché la lunghezza dell’anello è costante, non ci causerà alcun problema.

Nel nostro esempio definiremo 3 chiavi: a, b e c. Applichiamo f su ciascuna di esse. Supponiamo di avere i seguenti risultati:

• f(a) = 1
• f(a) = 5
• f(a) = 7

Quindi, possiamo posizionare le chiavi sull’anello in questo modo:

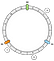
Come associamo una data chiave ad un nodo? La logica principale è quella di andare avanti. Da una data chiave, restituiamo il primo nodo che troviamo successivo mentre avanziamo:

In questo esempio, associamo a a N1, b e c a N2.

Ora, vediamo come viene gestito il ribilanciamento. Definiamo un altro nodo N3. Dove dobbiamo posizionarlo? Non c’è più spazio perché la distribuzione complessiva sia uniforme. Dobbiamo riorganizzare i nodi? No, altrimenti non saremmo più coerenti, vero? Per posizionare un nodo, riutilizziamo la stessa funzione di hashing f che abbiamo introdotto. Invece di essere chiamata con una chiave, può essere chiamata con un identificatore di nodo. Così la posizione del nuovo nodo è decisa in modo casuale.

Si pone allora una domanda: cosa dobbiamo fare con a dato che il prossimo nodo non è più N1:

La soluzione è la seguente: dobbiamo cambiare la sua associazione e far sì che a sia associato a N3:

Come abbiamo discusso precedentemente, un algoritmo ideale dovrebbe riequilibrare 1/n per cento delle chiavi in media. Nel nostro esempio, poiché stiamo aggiungendo un quarto nodo, dovremmo avere il 25% delle chiavi possibili riassociate a N3. È questo il caso?

• N0 dagli indici 8 a 12: 33,3% delle chiavi totali
• N1 dagli indici 2 a 4: 16,6% delle chiavi totali
• N2 dagli indici 4 a 8: 33.3% del totale delle chiavi
• N3 dagli indici 0 a 2: 16,6% del totale delle chiavi

La distribuzione non è uniforme. Come possiamo migliorarla? La soluzione è usare i nodi virtuali.

Diciamo che invece di posizionare un solo punto per nodo, possiamo posizionarne tre. Inoltre, dobbiamo definire tre diverse funzioni di hashing. Ogni nodo è hashato tre volte in modo da ottenere tre indici diversi:

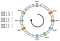
Possiamo applicare lo stesso algoritmo andando avanti. Tuttavia, una chiave sarebbe associata a un nodo indipendentemente dal nodo virtuale che ha incontrato.

In questo stesso esempio, la distribuzione sarebbe ora la seguente:

• N0: 33,3%
• N1: 25%
• N2: 41,6%

Più nodo virtuale definiamo per nodo, più la distribuzione dovrebbe essere uniforme. In media, con 100 nodi virtuali per server, la distribuzione standard è circa il 10%. Con 1000, è circa il 3,2%.

Questo meccanismo è anche utile se abbiamo nodi con dimensioni diverse. Per esempio, se un nodo è configurato per gestire teoricamente due volte il carico degli altri, potremmo far girare il doppio dei nodi virtuali.

Tuttavia, il principale svantaggio dei nodi virtuali è l’impronta di memoria. Se dobbiamo gestire migliaia di server, sarebbero necessari megabyte di memoria.

Prima di andare avanti, è interessante notare che a volte un algoritmo può essere sostanzialmente migliorato cambiando una piccola parte. Questo è il caso per esempio di un algoritmo pubblicato da Google nel 2017 chiamato hashing coerente con carichi limitati. Questa versione si basa sulla stessa idea di anello che abbiamo descritto. Tuttavia, il loro approccio è quello di eseguire un piccolo riequilibrio su ogni aggiornamento (una nuova chiave o un nodo aggiunto/cancellato). Questa versione supera quella originale in termini di deviazione standard con il compromesso di una complessità temporale peggiore.

Jump Consistent Hash

Nel 2007, due ingegneri di Google hanno pubblicato jump consistent hash. Rispetto all’algoritmo ad anello, questa implementazione “non richiede stoccaggio, è più veloce e fa un lavoro migliore nel dividere uniformemente lo spazio chiave tra i bucket e nel dividere uniformemente il carico di lavoro quando il numero di bucket cambia”. Detto diversamente, migliora la distribuzione del carico di lavoro tra i nodi (un bucket è lo stesso concetto di un nodo) senza alcun sovraccarico di memoria.

Ecco l’algoritmo in C++ (7 righe di codice 🤯):

In ring consistent hash, con 1000 nodi virtuali la deviazione standard era circa il 3,2%. Nel jump consistent hash, non abbiamo più bisogno del concetto di nodi virtuali. Tuttavia, la deviazione standard rimane inferiore allo 0,0000001%.

C’è però una limitazione. I nodi devono essere numerati in modo sequenziale. Se abbiamo una lista di server foo, bar e baz, non possiamo rimuovere bar per esempio. Tuttavia, se configuriamo un negozio di dati, possiamo applicare l’algoritmo per ottenere l’indice shard basato sul numero totale di shard. Pertanto, il salto coerente dell’hash può essere utile nel contesto dello sharding ma non del bilanciamento del carico.

Qual è l’algoritmo di hashing coerente perfetto?

Allora che abbiamo un po’ di esperienza con l’hashing coerente, facciamo un passo indietro e vediamo quale sarebbe l’algoritmo perfetto:

• Solo l’1/n per cento delle chiavi verrebbe rimappato in media dove n è il numero di nodi.
• Una complessità spaziale O(n) dove n è il numero di nodi.
• Una complessità di tempo O(1) per inserimento/rimozione di un nodo e per ricerca della chiave.
• Una deviazione standard minima per assicurarsi che un nodo non sia sovraccarico rispetto ad un altro.
• Permetterebbe di associare un peso ad un nodo per far fronte al diverso dimensionamento dei nodi.
• Permetterebbe un nome arbitrario dei nodi (non numerati in sequenza) per supportare sia il bilanciamento del carico che lo sharding.

Purtroppo, questo algoritmo non esiste. Sulla base di ciò che abbiamo visto:

• Rendezvous ha una complessità temporale lineare per lookup.
• Ring consistent hash ha una scarsa deviazione standard minima senza il concetto di nodi virtuali. Con i nodi virtuali, la complessità spaziale è O(n*v) con n il numero di nodi e v il numero di nodi virtuali per nodo.
• Jump consistent hash non ha una complessità temporale costante e non supporta il nome di nodi arbitrari.

L’argomento è ancora aperto e ci sono studi recenti che meritano di essere visti. Per esempio, l’hash coerente multi-sonda rilasciato nel 2005. Supporta la complessità spaziale O(1). Eppure, per ottenere una deviazione standard di ε, richiede O(1/ε) di tempo per lookup. Per esempio, se vogliamo ottenere una deviazione standard inferiore allo 0,5%, richiede l’hashing della chiave circa 20 volte. Pertanto, possiamo ottenere una deviazione standard minima, ma nello sforzo di una maggiore complessità del tempo di ricerca.

Come abbiamo detto nell’introduzione, gli algoritmi di hashing coerente sono diventati mainstream. Ora è usato in innumerevoli sistemi come MongoDB, Cassandra, Riak, Akka, ecc. sia nel contesto del bilanciamento del carico o della distribuzione dei dati. Eppure, come spesso nell’informatica, ogni soluzione ha dei compromessi.

Parlando di compromessi, se avete bisogno di un seguito, potete dare un’occhiata all’eccellente post scritto da Damian Gryski: