Funzione di Green

In generale, una funzione di Green è un kernel integrale che può essere usato per risolvere equazioni differenziali di un gran numero di famiglie, compresi esempi più semplici come le equazioni differenziali ordinarie con condizioni di valore iniziale o al contorno, così come esempi più difficili come le equazioni differenziali parziali (PDE) disomogenee con condizioni al contorno. Importanti per una serie di ragioni, le funzioni di Green permettono interpretazioni visive delle azioni associate a una fonte di forza o a una carica concentrata in un punto (Qin 2014), rendendole così particolarmente utili in aree della matematica applicata. In particolare, i metodi delle funzioni di Green sono ampiamente utilizzati in, ad es, fisica e ingegneria.

Più precisamente, dato un operatore differenziale lineare che agisce sulla collezione di distribuzioni su un sottoinsieme di un qualche spazio euclideo , una funzione di Green nel punto corrispondente a è una qualsiasi soluzione di

(1)

dove indica la funzione delta. La motivazione per definire una tale funzione è diffusa, ma moltiplicando l’identità di cui sopra per una funzione e integrando rispetto a si ottiene

(2)

La parte destra si riduce semplicemente a per le proprietà della funzione delta, e poiché è un operatore lineare che agisce solo su e non su , il lato sinistro può essere riscritto come

(3)

Questa riduzione è particolarmente utile quando si risolve nelle equazioni differenziali della forma

(4)

dove la precedente aritmetica conferma che

(5)

e da cui segue che ha la forma integrale specifica

(6)

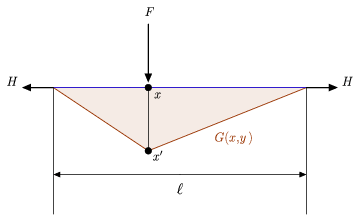
La figura sopra illustra sia l’interpretazione fisica intuitiva di una funzione di Green che un’equazione differenziale associata relativamente semplice con cui confrontare la definizione di cui sopra (Hartmann 2013). In particolare, mostra una corda tesa di lunghezza sospesa tra due pareti, tenuta in posizione da una forza orizzontale identica applicata su ciascuna delle sue estremità, e un carico laterale posto in qualche punto interno sulla corda. Sia il punto corrispondente a sulla corda deviata, supponiamo che la forza verso il basso sia costante, diciamo , e che indichi la deformazione della corda. A questo sistema fisico corrisponde l’equazione differenziale

(7)

per con , un sistema la cui semplicità permette di scrivere esplicitamente sia la sua soluzione che la sua funzione di Green :

(8)

e

(9)

rispettivamente. Come dimostrato nella figura precedente, la corda spostata ha il formato lineare a tratti dato da sopra, confermando così l’affermazione che la funzione di Green associata a questo sistema rappresenta l’azione della corda orizzontale corrispondente all’applicazione di una forza .

Una funzione di Green che prende una coppia di argomenti è talvolta indicata come una funzione di Green a due punti. Questo è in contrasto con le funzioni di Green a più punti che sono di particolare importanza nell’area della teoria dei molti corpi.

Come esempio elementare di una funzione a due punti come definita sopra, si consideri il problema di determinare il potenziale generato da una distribuzione di carica la cui densità di carica è , dove l’applicazione dell’equazione di Poisson e della legge di Coulomb al potenziale a prodotto da ogni elemento di carica dà una soluzione

(10)

che tiene, sotto certe condizioni, nella regione in cui . Poiché il lato destro può essere visto come un operatore integrale che converte in , si può riscrivere questa soluzione in termini di una funzione di Green avente la forma

(11)

dove la soluzione può essere riscritta:

(12)

(Arfken 2012).

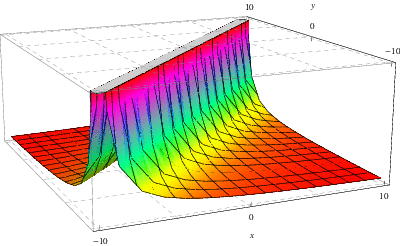
La figura sopra mostra la funzione di Green associata alla soluzione dell’equazione – discussa sopra dove qui, e , rispettivamente , è tracciata sull’asse -, rispettivamente -.

Una lista piuttosto completa di funzioni di Green corrispondenti a varie equazioni differenziali è mantenuta online da Kevin Cole (Cole 2000).

A causa della moltitudine di letteratura scritta sulle funzioni di Green, possono emergere diverse notazioni e definizioni, alcune delle quali sono topicamente diverse dalle precedenti ma che in generale non influenzano le importanti proprietà dei risultati. Come illustra l’esempio precedente, per esempio, alcuni autori preferiscono denotare le variabili e in termini di vettori e per sottolineare il fatto che sono elementi di per qualche che può essere maggiore di 1 (Arfken 1985). È anche relativamente comune vedere la definizione con un segno negativo in modo che sia definita come la funzione per cui

(13)

ma poiché questa considerazione puramente fisica non ha alcun effetto sulla matematica sottostante, questo punto di vista è generalmente trascurato. Sono note anche diverse altre notazioni per una funzione di Green, alcune delle quali includono l’uso di una minuscola al posto di (Stakgold 1979) così come l’inclusione di una linea verticale al posto di una virgola, per esempio (Duffy 2001).

In altri casi, la letteratura presenta definizioni che sono intimamente connesse ai contesti in cui sono presentate. Per esempio, alcuni autori definiscono le funzioni di Green come funzioni che soddisfano un certo insieme di condizioni, per esempio l’esistenza su un particolare tipo di dominio, l’associazione con un operatore differenziale molto particolare , o la soddisfazione di un preciso insieme di condizioni al contorno. Uno degli esempi più comuni di questo tipo si trova nelle note di, per esempio, Speck, dove una funzione di Green è definita per soddisfare per i punti e per tutti i punti che giacciono nel confine di (Speck 2011). Questa particolare definizione presenta un kernel integrale corrispondente alla soluzione di un’equazione di Poisson generalizzata e quindi si troverebbe di fronte a ovvie limitazioni quando viene adattata ad un ambiente più generale. D’altra parte, tali esempi non sono privi di vantaggi. Nel caso dell’esempio di Poisson generalizzato di cui sopra, per esempio, ogni funzione di Green può essere divisa in modo che

(14)

dove e per il Laplaciano regolare (Hartman 2013). In tali situazioni, è noto come la soluzione fondamentale dell’equazione differenziale sottostante e è noto come la sua soluzione regolare; come tali, e sono talvolta chiamati rispettivamente le parti fondamentale e regolare di .

Alcune proprietà fondamentali di una funzione di Green generale seguono immediatamente (o quasi) dalla sua definizione e si trasmettono a tutte le istanze particolari. Per esempio, se il kernel dell’operatore non è banale, allora ci possono essere diverse funzioni di Green associate a un singolo operatore; di conseguenza, si deve mostrare cautela quando ci si riferisce a “la” funzione di Green. Le funzioni di Green soddisfano una simmetria contigua nei loro due argomenti così che

(15)

dove qui, è definito come la soluzione dell’equazione

(16)

Qui, è l’aggettivo di . Un corollario immediato di questo fatto è che per gli operatori autoadesivi , è simmetrico:

(17)

Questa identità è spesso chiamata principio di reciprocità e dice, in termini fisici, che la risposta a causata da una sorgente unitaria a è la stessa della risposta a dovuta a una forza unitaria a (Stakgold 1979).

La proprietà essenziale di qualsiasi funzione di Green è che fornisce un modo per descrivere la risposta di una soluzione di equazione differenziale arbitraria a qualche tipo di termine sorgente in presenza di un certo numero di condizioni al contorno (Arfken et al. 2012). Alcuni autori ritengono che una funzione di Green abbia un ruolo analogo nella teoria delle equazioni differenziali parziali a quello delle serie di Fourier nella soluzione delle equazioni differenziali ordinarie (Mikula e Kos 2006).

Per scenari più astratti, esiste una serie di concetti che servono come analoghi specifici del contesto della nozione di funzione di Green. Per esempio, nell’analisi funzionale, è spesso utile considerare una cosiddetta funzione di Green generalizzata che ha molte proprietà analoghe quando viene integrata in modo astratto rispetto ai funzionali piuttosto che alle funzioni. Infatti, tali generalizzazioni hanno prodotto un ramo completamente analogo dell’analisi teorica delle PDE e sono esse stesse al centro di una grande quantità di ricerche.