Cos’è la geometria analitica?
Che cos’è la geometria analitica?
La geometria analitica è una branca dell’algebra che viene usata per modellare oggetti geometrici – punti, linee (rette) e cerchi sono i più basilari di questi. La geometria analitica è una grande invenzione di Cartesio e Fermat.
Nella geometria analitica piana, i punti sono definiti come coppie ordinate di numeri, per esempio, (x, y), mentre le linee rette sono a loro volta definite come gli insiemi di punti che soddisfano equazioni lineari, vedi le eccellenti esposizioni di D. Pedoe o D. Brannan et al. Per esempio, per qualsiasi due punti distinti (x1, y1) e (x2, y2), esiste un’unica linea ax + by + c = 0 che passa per questi punti. I suoi coefficienti a, b, c possono essere trovati (fino a un fattore costante) dal sistema lineare di due equazioni
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
o direttamente dall’equazione del determinante
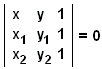 |
Tuttavia, nessuna teoria assiomatica può evitare di usare elementi indefiniti. Nella teoria degli insiemi che è alla base di gran parte della matematica e, in particolare, della geometria analitica, la nozione più fondamentale di insieme rimane indefinita.
La geometria dello spazio tridimensionale è modellata con triple di numeri (x, y, z) e un’equazione lineare 3D ax + by + cz + d = 0 definisce un piano. In generale, la geometria analitica fornisce un comodo strumento per lavorare in dimensioni superiori.
Nel quadro della geometria analitica si possono (e si modellano) anche geometrie non euclidee. Per esempio, nella geometria proiettiva piana un punto è una tripla di coordinate omogenee (x, y, z), non tutte 0, tali che
| (tx, ty, tz) = (x, y, z), |
per tutti i t ≠ 0, mentre una linea è descritta da un’equazione omogenea
| ax + bx + cz = 0. |
Nella geometria analitica, le sezioni coniche sono definite da equazioni di secondo grado:
| ax² + bxy + cy² + dx + ey + f = 0. |
La parte della geometria analitica che si occupa principalmente di equazioni lineari è chiamata algebra lineare.
La geometria analitica cartesiana è la geometria in cui gli assi x = 0 e y = 0 sono perpendicolari.
Le componenti della n-tupla x = (x1, …, xn) sono note come sue coordinate. Quando n = 2 o n = 3, la prima coordinata è chiamata ascissa e la seconda ordinata.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Contatto||Front page||Contenuti||Geometria||Up|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply