Campionamento di Gibbs

Un altro metodo MCMC

Come altri metodi MCMC, il campionatore di Gibbs costruisce una catena di Markov i cui valori convergono verso una distribuzione obiettivo. Il campionamento di Gibbs è infatti un caso specifico dell’algoritmo Metropolis-Hastings in cui le proposte sono sempre accettate.

Per approfondire, supponiamo di voler campionare una distribuzione di probabilità multivariata.

Nota: Una distribuzione di probabilità multivariata è una funzione di più variabili (cioè distribuzione normale a 2 dimensioni).

Non sappiamo come campionare direttamente da quest’ultima. Tuttavia, a causa di qualche convenienza matematica o forse solo per pura fortuna, ci capita di conoscere le probabilità condizionali.

Ecco dove entra in gioco il campionamento di Gibbs. Il campionamento di Gibbs è applicabile quando la distribuzione congiunta non è nota esplicitamente o è difficile da campionare direttamente, ma la distribuzione condizionale di ogni variabile è nota ed è più facile da campionare.

Iniziamo selezionando un valore iniziale per le variabili casuali X & Y. Poi, campioniamo dalla distribuzione condizionale di probabilità di X dato Y = Y⁰ denotata p(X|Y⁰). Nel passo successivo, campioniamo un nuovo valore di Y condizionato a X¹, che abbiamo appena calcolato. Ripetiamo la procedura per altre n – 1 iterazioni, alternando il prelievo di un nuovo campione dalla distribuzione di probabilità condizionata di X e dalla distribuzione di probabilità condizionata di Y, dato il valore corrente dell’altra variabile casuale.

Vediamo un esempio. Supponiamo di avere le seguenti distribuzioni di probabilità posteriori e condizionali.

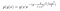
dove g(y) contiene i termini che non includono x, e g(x) contiene quelli che non dipendono da y.

Non conosciamo il valore di C (costante di normalizzazione). Tuttavia, conosciamo le distribuzioni di probabilità condizionali. Pertanto, possiamo usare il Campionamento di Gibbs per approssimare la distribuzione posteriore.

Nota: Le probabilità condizionali sono infatti distribuzioni normali, e possono essere riscritte come segue.

Viste le equazioni precedenti, procediamo a implementare l’algoritmo di Campionamento di Gibbs in Python. Per iniziare, importiamo le seguenti librerie.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Definiamo la funzione per la distribuzione posteriore (assumiamo C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Poi, tracciamo la distribuzione di probabilità.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Ora, tenteremo di stimare la distribuzione di probabilità usando il Campionamento di Gibbs. Come abbiamo detto in precedenza, le probabilità condizionali sono distribuzioni normali. Pertanto, possiamo esprimerle in termini di mu e sigma.

Nel seguente blocco di codice, definiamo le funzioni per mu e sigma, inizializziamo le nostre variabili casuali X & Y, e impostiamo N (il numero di iterazioni).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Passiamo attraverso l’algoritmo di Gibbs Sampling.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Finalmente, tracciamo i risultati.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Come possiamo vedere, la distribuzione di probabilità ottenuta usando l’algoritmo di Gibbs Sampling fa un buon lavoro di approssimazione della distribuzione obiettivo.

Conclusione

Il Campionamento di Gibbs è un metodo Monte Carlo a catena di Markov che estrae iterativamente un’istanza dalla distribuzione di ogni variabile, condizionata dai valori correnti delle altre variabili, al fine di stimare distribuzioni congiunte complesse. In contrasto con l’algoritmo Metropolis-Hastings, si accetta sempre la proposta. Così, il Campionamento di Gibbs può essere molto più efficiente.