Bilinear Filtering & Bilinear Interpolation

Guarda l’immagine qui sotto. Puoi calcolare i valori nei punti A, B e C?

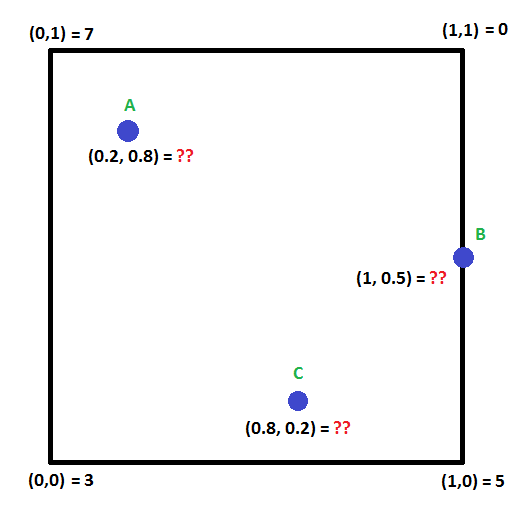
C’è una tecnica per fare questo chiamata interpolazione bilineare che estende l’idea di interpolazione lineare in due dimensioni.

Per calcolare l’interpolazione bilineare, basta fare l’interpolazione lineare su un asse e poi sull’altro.

Guardate questi esempi:

Punto A
Il punto A ha una coordinata di (0.2,0.8). Cominciamo con l’asse X.

Prima di tutto, faremo un’interpolazione attraverso la parte superiore del quadrato sull’asse X. Questo significa che abbiamo bisogno di andare 0,2 (20%) della strada da 7 a 0. Questo 0,2 è la nostra coordinata dell’asse X. Per calcolarlo facciamo così:
7 + (0-7) * 0.2 = 5.6

Prossimo, faremo l’interpolazione attraverso il fondo del quadrato sull’asse X. Quindi, come sopra, andremo a 0,2 (20%) del percorso da 3 a 5. Per calcolarlo facciamo così:
3 + (5-3) * 0.2 = 3.4

Ora che abbiamo interpolato attraverso il nostro asse X abbiamo bisogno di interpolare attraverso il nostro asse Y. Ora andremo 0,8 (80%) del percorso dal nostro valore inferiore (il valore di Y = 0), al nostro valore superiore (il valore di Y = 1). Il valore inferiore è l’interpolazione inferiore che abbiamo fatto (3,4) e il valore superiore è l’interpolazione superiore che abbiamo fatto (5,6).

Quindi, dobbiamo andare 0,8 (80%) della strada da 3,4 a 5,6. Per calcolarlo facciamo così:
3.4 + (5.6 – 3.4) * 0.8 = 5.16

Quindi, il valore al punto A è 5.16. L’immagine qui sotto dovrebbe aiutare a spiegare visivamente il processo che abbiamo seguito.

Punto B

Il punto B ha le coordinate di (1.0,0.5).

Iniziamo di nuovo con l’interpolazione dell’asse X (anche se si potrebbe facilmente iniziare con l’asse Y se si vuole! Si finirebbe con lo stesso risultato).

Facendo l’interpolazione dell’asse X attraverso l’alto, abbiamo bisogno di andare 1,0 (100%) della strada da 7 a 0. Sono sicuro che puoi indovinare qual è la risposta ma eccola calcolata:
7 + (0-7) * 1,0 = 0

Similmente, facciamo l’interpolazione dell’asse X attraverso il basso. Abbiamo bisogno di andare 1,0 (100%) della strada da 3 a 5.
3 + (5-3) * 1,0 = 5

Prossimamente viene l’interpolazione dell’asse Y. Dobbiamo passare 0,5 (50%) da 5 a 0.
5 + (0-5) * 0,5 = 2,5

Ecco fatto, il valore al punto B è 2,5. Anche questo dovrebbe avere senso guardando il diagramma. È fondamentalmente 1d interpolazione lineare tra 5 e 0, ed è a metà strada tra loro, quindi intuitivamente, la risposta 2.5 dovrebbe avere senso.

Punto C

Il punto C ha una coordinata di (0.8,0.2).

Di nuovo, facciamo l’interpolazione dell’asse X attraverso la parte superiore della scatola. Abbiamo bisogno di andare 0,8 (80%) della strada da 7 a 0.
7 + (0-7) * 0,8 = 1,4

Poi, dobbiamo fare l’interpolazione dell’asse x attraverso la parte inferiore della scatola. Dobbiamo andare 0,8 (80%) della strada da 3 a 5.
3 + (5-3) * 0,8 = 4,6

Infine, l’interpolazione dell’asse y. Dobbiamo passare 0,2 (20%) da 4,6 a 1,4.
4,6 + (1,4-4,6) * 0,2 = 3,96

Il valore del punto C è 3.96

Filtraggio bilineare

Mentre l’interpolazione bilineare è utile se hai una griglia di dati all’interno della quale vuoi interpolare i valori (come un campo di altezza che rappresenta il terreno?!), dove questo brilla veramente nello sviluppo dei giochi è nel filtraggio bilineare delle texture.

In pratica, quando avete una coordinata della texture che non si allinea perfettamente con il centro di un pixel nella texture (perché c’è un resto), usa la parte frazionaria della coordinata all’interno di quel pixel per fare un’interpolazione bilineare tra i 4 pixel coinvolti per ottenere il colore finale del pixel. Fa un’interpolazione bilineare su ciascuno dei canali: Rosso, Verde, Blu e Alfa.

Il risultato finale è piuttosto buono! Date un’occhiata all’immagine qui sotto per vederlo in azione su una texture che abbiamo ingrandito troppo. Il lato sinistro usa il filtraggio bilineare, mentre il lato destro non lo fa, e mostra solo il pixel più vicino.

Di conseguenza, il filtraggio bilineare delle texture deve fare 4 letture di pixel per essere in grado di interpolare tra loro, invece di una singola lettura di pixel come quando si fa il campionamento del pixel più vicino. Più letture di pixel = più overhead, e non così economico (computazionalmente) da usare.

Links

Per alcune persone che stanno leggendo questo, queste informazioni sono piuttosto basilari e potreste chiedervi perché mi sono preso la briga di scriverle. Guardate il prossimo post per qualcosa di bizzarro riguardante il filtraggio bilineare. Questo era necessario come trampolino di lancio per la prossima cosa che voglio mostrarvi ragazzi 😛

Wikipedia: Interpolazione lineare

Wikipedia: Interpolazione bilineare

Wikipedia: Filtraggio bilineare

Il lato oscuro del filtraggio bilineare

Guarda questi link per alcune informazioni più profonde su alcuni difetti (e alcuni rimedi) del campionamento bilineare basato sull’hardware:
iq: interpolazione hardware
iq: interpolazione texture migliorata