9.5 – Identificazione dei punti dati influenti

In questa sezione, impariamo le seguenti due misure per identificare i punti dati influenti:

• Differenza di adattamento (DFFITS)
• Distanze di Cook

L’idea di base di ciascuna di queste misure è la stessa, cioè eliminare le osservazioni una alla volta, ogni volta riadattando il modello di regressione sulle n-1 osservazioni rimanenti. Poi, confrontiamo i risultati utilizzando tutte le n osservazioni con i risultati con l’osservazione iesima eliminata per vedere quanta influenza ha l’osservazione sull’analisi. Analizzato in questo modo, siamo in grado di valutare l’impatto potenziale che ogni punto di dati ha sull’analisi di regressione.

Differenza nelle risposte (DFFITS)

La differenza nelle risposte per l’osservazione i, indicata come DFFITSi, è definita come:

\

Come si può vedere, il numeratore misura la differenza nelle risposte previste ottenute quando l’iesimo punto di dati è incluso ed escluso dall’analisi. Il denominatore è la deviazione standard stimata della differenza nelle risposte previste. Pertanto, la differenza di adattamento quantifica il numero di deviazioni standard che il valore montato cambia quando l’iesimo punto di dati viene omesso.

Un’osservazione è considerata influente se il valore assoluto del suo valore DFFITS è maggiore di:

dove, come sempre, n = il numero di osservazioni e k = il numero di termini predittori (cioè, il numero di parametri di regressione esclusa l’intercetta). È importante tenere a mente che questa non è una regola fissa, ma solo una linea guida! Non è difficile trovare diversi autori che usano una linea guida leggermente diversa. Pertanto, spesso preferisco una linea guida molto più soggettiva, come ad esempio un punto dati è considerato influente se il valore assoluto del suo valore DFFITS si distingue come un pollice dolente dagli altri valori DFFITS. Naturalmente, questo è un giudizio qualitativo, forse come dovrebbe essere, dato che gli outlier per loro stessa natura sono quantità soggettive.

Esempio #2 (di nuovo). Controlliamo la misura della differenza di adattamento per questo set di dati (influence2.txt):

Registrando y su x e richiedendo la differenza di adattamento, otteniamo il seguente output del software:

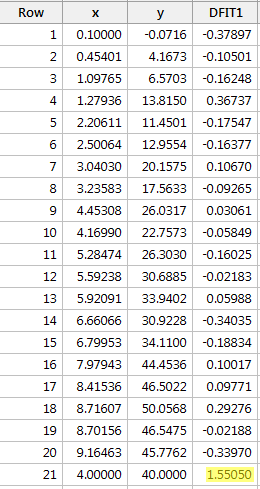
Utilizzando la linea guida oggettiva definita sopra, riteniamo che un punto dati sia influente se il valore assoluto del suo valore DFFITS è maggiore di:

\

Solo un punto dati – quello rosso – ha un valore DFFITS il cui valore assoluto (1.55050) è maggiore di 0,82. Pertanto, in base a questa linea guida, considereremo il punto dati rosso influente.

Esempio #3 (di nuovo). Controlliamo la misura della differenza di adattamento per questa serie di dati (influence3.txt):

Registrando y su x e richiedendo la differenza di adattamento, otteniamo il seguente output del software:

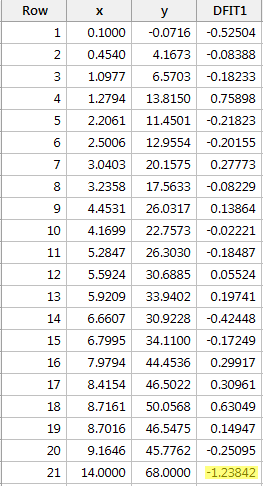
Utilizzando la linea guida oggettiva definita sopra, riteniamo che un punto dati sia influente se il valore assoluto del suo valore DFFITS è maggiore di:

\

Solo un punto dati – quello rosso – ha un valore DFFITS il cui valore assoluto (1.23841) è maggiore di 0,82. Pertanto, in base a questa linea guida, consideriamo il punto dati rosso influente.

Quando abbiamo studiato questa serie di dati all’inizio di questa lezione, abbiamo deciso che il punto dati rosso non ha influenzato molto l’analisi di regressione. Eppure, qui, la differenza nella misura dei fit suggerisce che è davvero influente. Cosa sta succedendo qui? Tutto si riduce a riconoscere che tutte le misure di questa lezione sono solo strumenti che segnalano punti di dati potenzialmente influenti per l’analista di dati. Alla fine, l’analista dovrebbe analizzare il set di dati due volte – una volta con e una volta senza i punti di dati segnalati. Se i punti di dati alterano significativamente il risultato dell’analisi di regressione, allora il ricercatore dovrebbe riportare i risultati di entrambe le analisi.

Incidentalmente, in questo esempio, se usiamo la linea guida più soggettiva se il valore assoluto del valore DFFITS spicca come un pollice dolente, probabilmente non considereremo il punto di dati rosso come influente. Dopo tutto, il prossimo valore DFFITS più grande (in valore assoluto) è 0,75898. Questo valore DFFITS non è poi così diverso dal valore DFFITS del nostro punto dati “influente”.

Esempio #4 (di nuovo). Controlliamo la misura della differenza di adattamento per questa serie di dati (influence4.txt):

Regressando y su x e richiedendo la differenza di adattamento, otteniamo il seguente output del software:

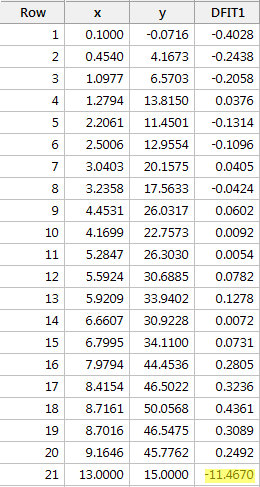
Utilizzando la linea guida oggettiva definita sopra, riteniamo di nuovo che un punto dati sia influente se il valore assoluto del suo valore DFFITS è maggiore di:

\

Che ne pensi? C’è qualcuno dei valori DFFITS che spicca come un pollice dolente? Errr – il valore DFFITS del punto dati rosso (-11.4670 ) è certamente di una grandezza diversa da tutti gli altri. In questo caso, ci dovrebbero essere pochi dubbi sul fatto che il punto dati rosso è influente!

Distanza di Cook

Solo saltando qui, la misura della distanza di Cook, indicata come Di, è definita come:

\.\]

Sembra un po’ confusa, ma la cosa principale da riconoscere è che la Di di Cook dipende sia dal residuo, ei (nel primo termine), sia dalla leva, hii (nel secondo termine). Cioè, sia il valore x che il valore y del punto dati giocano un ruolo nel calcolo della distanza di Cook.

In breve:

• Di riassume direttamente quanto cambiano tutti i valori montati quando l’iesima osservazione viene eliminata.
• Un punto di dati che ha un grande Di indica che il punto di dati influenza fortemente i valori adattati.

Indaghiamo su cosa significa esattamente questa prima affermazione nel contesto di alcuni dei nostri esempi.

Esempio #1 (ancora). Si può ricordare che il grafico di questi dati (influence1.txt) suggerisce che non ci sono outlier né punti di dati influenti per questo esempio:

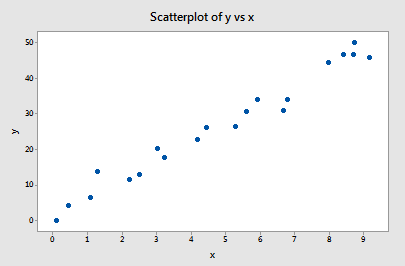
Se regrediamo y su x usando tutti gli n = 20 punti dati, determiniamo che il coefficiente di intercetta stimato b0 = 1,732 e il coefficiente di pendenza stimato b1 = 5,117. Se rimuoviamo il primo punto di dati dalla serie di dati e regrediamo y su x usando i restanti n = 19 punti di dati, determiniamo che il coefficiente di intercetta stimato b0 = 1,732 e il coefficiente di pendenza stimato b1 = 5,1169. Come speriamo e ci aspettiamo, le stime non cambiano molto quando si rimuove un punto di dati. Continuando questo processo di rimozione di ogni punto di dati uno alla volta, e tracciando le pendenze stimate risultanti (b1) contro le intercette stimate (b0), otteniamo:

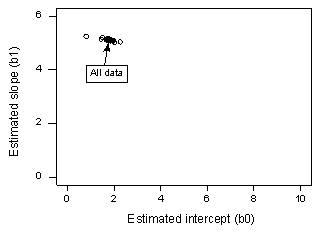
Il punto nero solido rappresenta i coefficienti stimati basati su tutti gli n = 20 punti dati. I cerchi aperti rappresentano ciascuno dei coefficienti stimati ottenuti eliminando ogni punto di dati uno alla volta. Come si può vedere, i coefficienti stimati sono tutti raggruppati insieme indipendentemente da quale punto di dati viene rimosso. Questo suggerisce che nessun punto di dati influenza indebitamente la funzione di regressione stimata o, a sua volta, i valori montati. In questo caso, ci aspetteremmo che tutte le misure della distanza di Cook, Di, siano piccole.

Esempio #4 (di nuovo). Si può ricordare che il grafico di questi dati (influence4.txt) suggerisce che un punto di dati è influente e un outlier per questo esempio:

Se regrediamo y su x usando tutti gli n = 21 punti dati, determiniamo che il coefficiente di intercetta stimato b0 = 8,51 e il coefficiente di pendenza stimato b1 = 3,32. Se rimuoviamo il punto rosso dalla serie di dati e regrediamo y su x usando i rimanenti n = 20 punti di dati, determiniamo che il coefficiente di intercetta stimato b0 = 1,732 e il coefficiente di pendenza stimato b1 = 5,1169. Wow, le stime cambiano sostanzialmente dopo la rimozione di un punto di dati. Continuando questo processo di rimozione di ogni punto di dati uno alla volta, e tracciando le pendenze stimate risultanti (b1) contro le intercette stimate (b0), otteniamo:

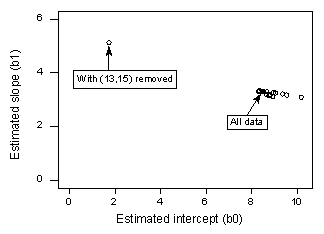
Ancora una volta, il punto nero solido rappresenta i coefficienti stimati basati su tutti gli n = 21 punti dati. I cerchi aperti rappresentano ciascuno dei coefficienti stimati ottenuti eliminando ogni punto di dati uno alla volta. Come si può vedere, con l’eccezione del punto dati rosso (x = 13, y = 15), i coefficienti stimati sono tutti raggruppati insieme indipendentemente da quale punto dati viene rimosso. Questo suggerisce che il punto di dati rosso è l’unico punto di dati che influenza indebitamente la funzione di regressione stimata e, a sua volta, i valori montati. In questo caso, ci aspetteremmo che la misura di distanza di Cook, Di, per il punto rosso sia grande e che le misure di distanza di Cook, Di, per gli altri punti dati siano piccole.

Utilizzando le misure di distanza di Cook. La bellezza degli esempi precedenti è la capacità di vedere cosa sta succedendo con semplici grafici. Sfortunatamente, non possiamo fare affidamento su semplici grafici nel caso della regressione multipla. Invece, dobbiamo affidarci alle linee guida per decidere quando una misura di distanza di Cook è abbastanza grande da giustificare il trattamento di un punto di dati come influente.

Ecco le linee guida comunemente usate:

• Se Di è maggiore di 0,5, allora l’iesimo punto di dati è degno di ulteriori indagini perché potrebbe essere influente.
• Se Di è maggiore di 1, allora l’iesimo punto di dati è molto probabilmente influente.
• Oppure, se Di spicca come un pollice dolente dagli altri valori Di, è quasi certamente influente.

Esempio #2 (ancora). Controlliamo la misura della distanza di Cook per questo set di dati (influence2.txt):

Regressando y su x e richiedendo le misure di distanza di Cook, otteniamo il seguente output del software:

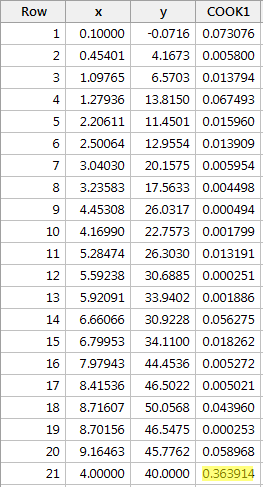
La misura di distanza di Cook per il punto dati rosso (0.363914) risalta un po’ rispetto alle altre misure di distanza di Cook. Tuttavia, la misura della distanza di Cook per il punto dati rosso è inferiore a 0,5. Pertanto, in base alla misura della distanza di Cook, non classificheremmo il punto dati rosso come influente.

Esempio #3 (di nuovo). Controlliamo la misura della distanza di Cook per questa serie di dati (influence3.txt):

Regressando y su x e richiedendo le misure di distanza di Cook, otteniamo il seguente output software:

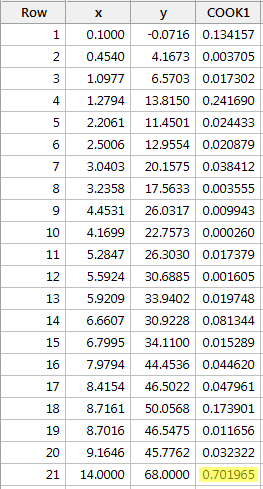
La misura di distanza di Cook per il punto dati rosso (0.701965) spicca un po’ rispetto alle altre misure di distanza di Cook. Tuttavia, la misura di distanza di Cook per il punto dati rosso è più grande di 0,5 ma meno di 1. Pertanto, sulla base della misura di distanza di Cook, potremmo forse indagare ulteriormente ma non necessariamente classificare il punto dati rosso come influente.

Esempio #4 (ancora). Controlliamo la misura di distanza di Cook per questa serie di dati (influence4.txt):

Regressando y su x e richiedendo le misure di distanza di Cook, otteniamo il seguente output del software:

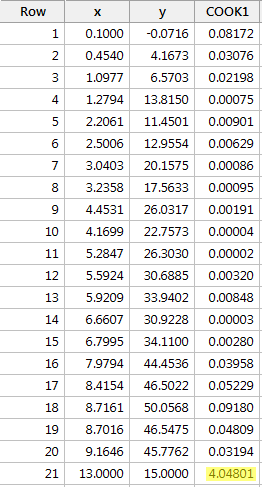
In questo caso, la misura di distanza di Cook per il punto dati rosso (4.04801) spicca sostanzialmente rispetto alle altre misure di distanza di Cook. Inoltre, la misura della distanza di Cook per il punto di dati rosso è maggiore di 1. Pertanto, sulla base della misura della distanza di Cook – e non sorprende – classificheremmo il punto di dati rosso come influente.

Un metodo alternativo per interpretare la distanza di Cook che viene talvolta utilizzato è quello di mettere in relazione la misura con la distribuzione F(k+1, n-k-1) e trovare il corrispondente valore percentile. Se questo percentile è inferiore a circa il 10 o 20 per cento, allora il caso ha poca influenza apparente sui valori montati. D’altra parte, se è vicino al 50% o anche più alto, allora il caso ha una grande influenza. (Qualsiasi cosa “in mezzo” è più ambigua.)