Mi az analitikus geometria?
Mi az analitikus geometria?
Az analitikus geometria az algebra egyik ága, amelyet geometriai objektumok modellezésére használnak – ezek közül a pontok, (egyenes) vonalak és körök a legalapvetőbbek. Az analitikus geometria Descartes és Fermat nagy találmánya.
A síkbeli analitikus geometriában a pontokat rendezett számpárokként definiáljuk, mondjuk (x, y), míg az egyeneseket viszont lineáris egyenleteket kielégítő pontok halmazaként definiáljuk, lásd D. Pedoe vagy D. Brannan és mások kiváló kifejtéseit. Az analitikus geometria szempontjából a geometriai axiómák levezethető tételek. Például bármely két különböző (x1, y1) és (x2, y2) pontra létezik egy ax + by + c = 0 egyenes, amely áthalad ezeken a pontokon. Ennek a, b, c együtthatói (egy konstans tényezőig) megtalálhatók a két egyenletből álló lineáris egyenletrendszerből
| ax1 + by1 + c = 0 ax2 + by2 + c = 0 , |
vagy közvetlenül a determináns egyenletből
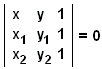 |
Mindenesetre egyetlen axiomatikus elmélet sem menekülhet meg a határozatlan elemek használata elől. A matematika nagy részének és különösen az analitikus geometriának alapjául szolgáló halmazelméletben a halmaz legalapvetőbb fogalma meghatározatlan marad.
A háromdimenziós tér geometriáját számhármasokkal (x, y, z) modellezzük, és egy 3D-s lineáris egyenlet ax + by + cz + d = 0 definiál egy síkot. Általában az analitikus geometria kényelmes eszközt nyújt a magasabb dimenziókban való munkához.
Az analitikus geometria keretein belül modellezhetünk (és modellezünk) nem-euklideszi geometriákat is. Például a síkbeli projektív geometriában egy pont a homogén koordináták (x, y, z) olyan hármasa (nem mind 0), hogy
| (tx, ty, tz) = (x, y, z), |
minden t ≠ 0-ra, míg egy egyenest egy homogén egyenlet ír le
| ax + bx + cz = 0. |
Az analitikus geometriában a kúpszögmetszeteket másodfokú egyenletek határozzák meg:
| ax² + bxy + cy² + dx + ey + f = 0. |
Az analitikus geometria azon részét, amely leginkább lineáris egyenletekkel foglalkozik, lineáris algebrának nevezzük.
A kartéziánus analitikus geometria az a geometria, amelyben az x = 0 és y = 0 tengelyek merőlegesek egymásra.
Az x = (x1, …, xn) n-pár összetevőit koordinátáknak nevezzük. Ha n = 2 vagy n = 3, akkor az első koordinátát abszcisszának, a másodikat ordinátának nevezzük.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Contact|||Front page|||Contents||Geometry||Up|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply