Matematika a szabad bölcsészet számára
Learning Outcomes
- Meghatározni és azonosítani a geometriai formák, növények önhasonlóságát, és geológiai képződmények
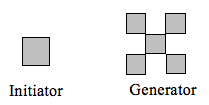
- Generálni egy fraktál alakzatot egy indító és egy generátor segítségével
- Méretezni egy geometriai objektumot egy adott méretezési tényezővel a méretezési dimenzió összefüggés segítségével
- Meghatározni egy fraktál objektum fraktáldimenzióját
A fraktálok a vizuális önhasonlóság mellett más érdekes tulajdonságokkal is rendelkeznek. Vegyük például észre, hogy a Sierpinski-tömítés iterációjának minden egyes lépése a fennmaradó terület egynegyedét távolítja el. Ha ezt a folyamatot a végtelenségig folytatnánk, akkor a végén lényegében az egész területet eltávolítanánk, ami azt jelenti, hogy egy kétdimenziós területtel kezdtük, és valahogy a végén valami ennél kisebbet kapunk, de látszólag többet, mint egy egydimenziós vonal.
Ahhoz, hogy ezt az elképzelést megvizsgáljuk, beszélnünk kell a dimenzióról. Valami, például egy vonal 1 dimenziós; csak hossza van. Bármilyen görbe 1 dimenziós. Az olyan dolgok, mint a dobozok és a körök 2 dimenziósak, mivel van hosszuk és szélességük, ami egy területet ír le. Az olyan tárgyak, mint a dobozok és a hengerek hosszúsággal, szélességgel és magassággal rendelkeznek, ami egy térfogatot ír le, és 3 dimenziósak.
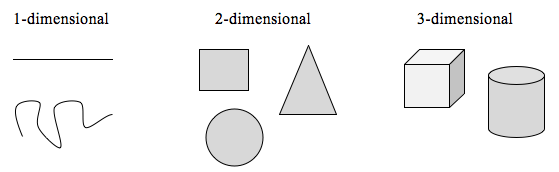
A tárgyak méretezésére bizonyos szabályok vonatkoznak, amelyek a dimenziójukkal kapcsolatosak.
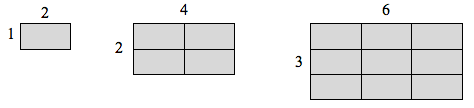
Ha lenne egy 1 hosszúságú egyenesem, és a hosszát 2-vel akarnám méretezni, akkor az eredeti egyenes két példányára lenne szükségem. Ha lenne egy 1 hosszúságú vonalam, és a hosszát 3-mal akarnám méretezni, akkor az eredeti három példányára lenne szükségem.
Ha lenne egy téglalapom, amelynek hossza 2, magassága 1, és a hosszát és szélességét 2-vel akarnám méretezni, akkor az eredeti téglalap négy példányára lenne szükségem. Ha a hosszát és a szélességét 3-mal akarnám méretezni, akkor az eredeti téglalap kilenc példányára lenne szükségem.
Ha lenne egy kocka, amelynek oldalai 1 hosszúak, és a hosszát és szélességét 2-vel akarnám méretezni, akkor az eredeti kocka nyolc példányára lenne szükségem. Ha a hosszát és szélességét 3-mal akarnám méretezni, akkor az eredeti kocka 27 példányára lenne szükségem.
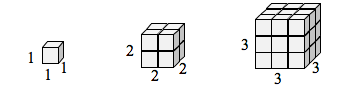
Megjegyezzük, hogy az 1 dimenziós esetben a szükséges példányok = méretarány.
A 2 dimenziós esetben a szükséges példányok = méretarány^{2}.
A 3 dimenziós esetben a szükséges példányok = méretarány^{3}.
A példákból következtethetünk egy mintára.
Méretezés-dimenzió összefüggés
Egy D-dimenziós alakzat S méretezési tényezővel való méretezéséhez az eredeti alakzat szükséges C példányainak száma a következő lesz:
\text{Copies}=\text{Scale}^{\text{Dimension}}, vagy C=S^{D}
Példa
A méretezés-dimenzió összefüggést használjuk a Sierpinski-tömítés méretének meghatározására.
Tegyük fel, hogy az eredeti tömítés oldalhosszúságát 1. Az ábrázolt nagyobb tömítés kétszer olyan széles és kétszer olyan magas, tehát 2-szeresére méreteztük.
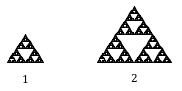
Megjegyezzük, hogy a nagyobb tömítés megépítéséhez az eredeti tömítés 3 példányára van szükség.
A C=S^{D} méretezési-dimenzió összefüggést felhasználva megkapjuk a 3=2^{D} egyenletet.
Mivel 2^{1}=2 és 2^{2}=4, azonnal láthatjuk, hogy D valahol 1 és 2 között van; a tömítés több mint 1 dimenziós alakzat, de annyi területet vettünk el, hogy az már kevesebb, mint 2 dimenziós.
A 3=2^{D} egyenlet megoldásához logaritmusokra van szükség. Ha korábban tanultál logaritmusokat, akkor talán emlékszel, hogyan kell megoldani ezt az egyenletet (ha nem, akkor ugorj az alábbi dobozba, és használd ezt a képletet a számológép log gombjával):
Vegyük mindkét oldal logaritmusát.
3={{2}^{D}}}
A logaritmusok exponens tulajdonságát használd.
\log(3)=\log\left({{2}^{D}}}\right)
Osszuk el log(2)-vel.
\log(3)=D\log\left(2\right)
A tömítés mérete körülbelül 1,585.
D=\frac{\log\left(3\right)}{\log(2)}\approx1.585
Méretezés-dimenzió összefüggés, a dimenzió megtalálásához
Egy fraktál D dimenziójának megtalálásához meg kell határozni az S méretezési tényezőt és az eredeti alakzat szükséges C példányainak számát, majd használjuk a képletet
D=\frac{\log\left(C\right)}{\log(S)}
Kipróbáljuk
Meghatározzuk az iniciátor és a generátor segítségével előállított fraktál dimenzióját.
A következő videóban egy kidolgozott példát mutatunk be a Sierpinski-tömítés dimenziójának meghatározására
.

Leave a Reply