Introducing Consistent Hashing

Az elosztott architektúrák elterjedésével a konzisztens hashing általánossá vált. De mi is ez pontosan, és miben különbözik a szabványos hashing algoritmustól? Mik a pontos motivációk mögötte?
Először ismertetjük a főbb fogalmakat. Ezután beleássuk magunkat a meglévő algoritmusokba, hogy megértsük a konzisztens hasheléssel kapcsolatos kihívásokat.
Hashing
A hashelés a tetszőleges méretű adatok fix méretű értékekre való leképezésének folyamata. Minden létező algoritmusnak megvan a maga specifikációja:
- MD5 128 bites hash-értékeket állít elő.
- SHA-1 160 bites hash-értékeket állít elő.
- stb.
A zárolásnak számos alkalmazása van az informatikában. Az egyik ilyen alkalmazás például az úgynevezett ellenőrző összeg. Egy adathalmaz integritásának ellenőrzésére használhatunk hash-algoritmust. Egy kiszolgáló hash-olja az adathalmazt, és a hash-értéket jelzi az ügyfélnek. Ezután az ügyfél az adatkészlet saját verzióját hash-olja, és összehasonlítja a hash-értékeket. Ha azok megegyeznek, akkor az integritást ellenőrizni kell.
A “kell” itt fontos. A legrosszabb esetben ütközés következik be. Az ütközés az, amikor két különböző adatnak ugyanaz a hash-értéke. Vegyünk egy valós példát a következő hash-függvény definiálásával: Adott egy személy, ez visszaadja a születési dátumát (születési nap & születési hónap). A születésnapi paradoxon azt mondja, hogy ha csak 23 ember van egy szobában, akkor annak a valószínűsége, hogy két személynek ugyanaz a születésnapja (tehát ütközés) több mint 50%. Ezért a születésnap függvény valószínűleg nem jó hashing függvény.

A hashing gyors bevezetéseként fontos megérteni, hogy a fő gondolat az értékek szétterítéséről szól egy tartományban. Például:
- MD5 szétteríti az értékeket egy 128 bites tartományban
- Egy 32 elemű tömb által támogatott hashtable (vagy hashmap) rendelkezik egy belső hashing függvénnyel, amely szétteríti az értékeket bármely indexre (0-tól 31-ig).
Leterheléselosztás
A terheléselosztást úgy lehet definiálni, mint a terhelés csomópontok közötti elosztásának folyamatát. A csomópont kifejezés itt felcserélhető a szerverrel vagy a példánnyal. Ez egy számítási egység.
A terheléselosztás egyik példája a terheléselosztás. Feladatok egy halmazának egy erőforráshalmazon való elosztásáról van szó. A terheléselosztást például arra használjuk, hogy az API-kéréseket elosztjuk a webkiszolgáló példányok között.
Amikor adatokról van szó, inkább a sharding kifejezést használjuk. Az adatbázis shard egy adatbázisban lévő adatok horizontális partíciója. Tipikus példa erre egy három shardra particionált adatbázis, ahol minden shard az összes adat egy-egy részhalmazát tartalmazza.
A terheléselosztás és a sharding közös kihívásokban osztozik. Az adatok egyenletes elosztása például annak biztosítása érdekében, hogy egy csomópont ne legyen túlterhelt a többihez képest. Bizonyos kontextusban a terheléselosztás és a sharding azt is igényli, hogy a feladatokat vagy az adatokat folyamatosan ugyanahhoz a csomóponthoz rendeljük:
- Ha egy adott fogyasztó műveleteit kell szerializálni, egyenként kezelni, akkor a kérést ugyanahhoz a csomóponthoz kell irányítanunk.
- Ha adatokat kell elosztani, akkor tudnunk kell, hogy egy adott kulcshoz melyik shard a tulajdonos.
Az ismerősen hangzik? Ebben a két példában értékeket osztunk szét egy tartományban. Legyen szó a kiszolgáló csomópontokra szétosztott feladatról vagy az adatbázis shardokra szétosztott adatokról, visszatalálunk a hasheléssel kapcsolatos gondolathoz. Ez az oka annak, hogy a hashing a terheléselosztással együtt használható. Lássuk, hogyan.
Mod-n Hashing
A mod-n hashing elve a következő. Minden kulcsot egy hash-függvény segítségével hash-zsaluzunk, hogy a bemenetet egész számmá alakítsuk át. Ezután a csomópontok száma alapján modulálást végzünk.
Lássunk egy konkrét példát 3 csomóponttal. Itt a terhelést egy kulcsazonosító alapján kell elosztanunk e csomópontok között. Minden kulcsot hash-eljük, majd modulo műveletet végzünk:

Ez a megközelítés előnye az állapotmentesség. Nem kell semmilyen állapotot tartanunk, amely emlékeztetne minket arra, hogy a foo a 2. csomóponthoz lett továbbítva. Mégis tudnunk kell, hogy hány csomópont van beállítva a modulo művelet alkalmazásához.
Aztán hogyan működik a mechanizmus ki- vagy beléptetés (csomópontok hozzáadása vagy eltávolítása) esetén? Ha hozzáadunk egy újabb csomópontot, akkor a modulo művelet most 3 helyett 4 alapján történik:

Mint látjuk, a foo és baz kulcsok már nem ugyanahhoz a csomóponthoz tartoznak. A mod-n hasheléssel nem garantálható a kulcs/csomópont társítás konzisztenciájának fenntartása. Ez probléma? Lehetséges.
Mi van, ha egy adattárolót valósítunk meg sharding használatával és a mod-n stratégián alapuló adatelosztással? Ha skálázzuk a csomópontok számát, akkor újraegyensúlyozási műveletet kell végrehajtanunk. Az előző példában az újrakiegyenlítés a következőket jelenti:
- A
fooátmozgatása a 2-es csomópontról a 0. csomópontra. - A
bazátmozgatása a 2-es csomópontról a 3-as csomópontra.
Most mi történik, ha több millió vagy akár milliárdnyi adatot tároltunk, és szinte mindent újra kell kiegyensúlyoznunk? Ahogy azt el tudjuk képzelni, ez egy nehézkes folyamat lenne. Ezért meg kell változtatnunk a terheléselosztási technikánkat, hogy az újbóli kiegyensúlyozáskor:
- Az elosztás a lehető legegyenletesebb maradjon az új csomópontok száma alapján.
- A migrálandó kulcsok számát korlátozni kell. Ideális esetben ez csak a kulcsok 1/n százaléka lenne, ahol n a csomópontok száma.
A konzisztens hashing algoritmusoknak pontosan ez a célja.
A konzisztens kifejezés azonban kissé zavaró lehet. Találkoztam olyan mérnökökkel, akik azt feltételezték, hogy az ilyen algoritmusok a skálázhatóság ellenére is folyamatosan ugyanahhoz a csomóponthoz társítanak egy adott kulcsot. Ez nem így van. Egy bizonyos pontig konzisztensnek kell lennie ahhoz, hogy az eloszlás egyenletes maradjon.
Most itt az ideje, hogy beleássuk magunkat néhány megoldásba.
Rendezvous
Aendezvous volt az első algoritmus, amelyet a problémánk megoldására javasoltak. Bár az eredeti, 1996-ban publikált tanulmány nem említi a konzisztens hashing kifejezést, megoldást kínál az általunk leírt kihívásokra. Lássunk egy lehetséges megvalósítást Go nyelven:
Hogyan működik? Minden egyes csomópontot bejárunk, és kiszámítjuk a hash-értékét. A hash-értéket egy hash függvény adja vissza, amely egy kulcs (a bemenetünk) és egy csomópont-azonosító alapján egész számot állít elő (a legegyszerűbb megközelítés, ha a két karakterlánc összekapcsolását hash-eljük). Ezután visszaadjuk a legmagasabb hash-értékkel rendelkező csomópontot. Ez az oka annak, hogy az algoritmust a legnagyobb véletlen súlyú hashelésnek is nevezik.
A randevú fő hátránya az O(n) időbonyolultsága, ahol n a csomópontok száma. Nagyon hatékony, ha korlátozott számú csomópontra van szükségünk. Ha azonban ezer csomópontot kezdünk el fenntartani, akkor teljesítményproblémákat okozhat.
Ring Consistent Hash
A következő algoritmust 1997-ben Karger és társai adták ki ebben a cikkben. Ez a tanulmány említette először a konzisztens hashelés kifejezést.
Ez egy gyűrűn (egy végponttól végpontig összefüggő tömb) alapul. Bár ez a legnépszerűbb konzisztens hashing algoritmus (vagy legalábbis a legismertebb), az elvét nem mindig értik jól. Merüljünk el benne.
Az első művelet a gyűrű létrehozása. A gyűrűnek fix hosszúsága van. Példánkban 12 részre osztjuk fel:

Ezután elhelyezzük a csomópontjainkat. Példánkban N0, N1 és N2 fogjuk meghatározni.
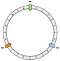
A csomópontokat egyelőre egyenletesen osztjuk el. Erre a későbbiekben még visszatérünk.
Aztán ideje megnézni, hogyan ábrázoljuk a kulcsokat. Először is szükségünk van egy ffüggvényre, amely egy kulcs alapján visszaad egy gyűrűindexet (0-tól 11-ig). Ehhez használhatjuk a mod-n hashinget. Mivel a gyűrű hossza állandó, ez nem fog nekünk problémát okozni.
Példánkban 3 kulcsot fogunk definiálni: a, b és c. Mindegyikre alkalmazzuk a f kulcsot. Tegyük fel, hogy a következő eredményeket kapjuk:
f(a) = 1f(a) = 5f(a) = 7
Ezért a kulcsokat így tudjuk elhelyezni a gyűrűn:
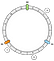
Hogyan rendelünk egy adott kulcsot egy csomóponthoz? A fő logika az előrehaladás. Egy adott kulcsból visszaadjuk az első csomópontot, amelyet a továbbhaladás során legközelebb találunk:

Ebben a példában a a-hez N1, b és c-hez N2 társítjuk.
Most nézzük, hogyan történik az újraegyensúlyozás. Definiálunk egy másik csomópontot N3. Hová pozícionáljuk? Már nincs hely arra, hogy a teljes eloszlás egyenletes legyen. Át kellene szerveznünk a csomópontokat? Nem, különben már nem lennénk egységesek, nem igaz? Egy csomópont pozícionálásához újra felhasználjuk ugyanazt a f hashing függvényt, amit bevezettünk. Ahelyett, hogy egy kulccsal hívnánk meg, egy csomópont-azonosítóval hívhatjuk meg. Így az új csomópont pozíciója véletlenszerűen dől el.
Ezután felmerül egy kérdés: mit kezdjünk a a-el, hiszen a következő csomópont már nem N1:

A megoldás a következő: N3:

Amint korábban tárgyaltuk, egy ideális algoritmusnak átlagosan a kulcsok 1/n százalékát kell újra kiegyensúlyoznia. Példánkban, mivel hozzáadunk egy negyedik csomópontot, a lehetséges kulcsok 25 százalékát kellene újraszerveznünk a N3-hoz. Ez így van?
-
N0a 8-12. indexekből: az összes kulcs 33,3%-a -
N1a 2-4. indexekből: az összes kulcs 16,6%-a -
N2a 4-8. indexekből: 33.Az összes kulcs -
N33%-a a 0-tól 2-ig terjedő indexekből: az összes kulcs
16,6%-a Az eloszlás nem egyenletes. Hogyan javíthatnánk ezen? A megoldás a virtuális csomópontok használata.
Tegyük fel, hogy ahelyett, hogy csomópontonként egyetlen pontot helyeznénk el, három pontot helyezhetünk el. Továbbá három különböző hashing függvényt kell definiálnunk. Minden csomópontot háromszor hasheljük, így három különböző indexet kapunk:
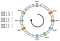
Előre haladva ugyanezt az algoritmust alkalmazhatjuk. Mégis, egy kulcsot egy csomóponthoz rendelnénk, függetlenül attól, hogy milyen virtuális csomóponttal találkozott.
Éppen ebben a példában az eloszlás most a következő lenne:
-
N0: 33,3% -
N1: 25% -
N2: 41,6%
Minél több virtuális csomópontot határozunk meg csomópontonként, annál inkább egyenletesnek kell lennie az eloszlásnak. Átlagosan, kiszolgálónként 100 virtuális csomópont esetén az egyenletes eloszlás körülbelül 10%. 1000-nél ez körülbelül 3,2%.
Ez a mechanizmus akkor is hasznos, ha különböző méretű csomópontjaink vannak. Ha például egy csomópontot úgy konfigurálunk, hogy elméletileg kétszer akkora terhelést tudjon kezelni, mint a többi, akkor kétszer annyi virtuális csomópontot pörgethetünk fel.
A virtuális csomópontok fő hátránya azonban a memóriaterület. Ha több ezer szervert kellene kezelnünk, akkor ez megabájtnyi memóriát igényelne.
Mielőtt továbblépnénk, érdekes megjegyezni, hogy néha egy algoritmus lényegesen javítható egy kis rész megváltoztatásával. Ez a helyzet például a Google által 2017-ben közzétett, konzisztens hashelés korlátos terheléssel nevű algoritmus esetében. Ez a változat ugyanarra a gyűrűs ötletre épül, amit mi is leírtunk. Mégis, az ő megközelítésük az, hogy minden frissítés (új kulcs vagy csomópont hozzáadása/törlése) esetén egy kis újrakiegyenlítést hajtanak végre. Ez a változat a szórás tekintetében felülmúlja az eredetit, a legrosszabb időbonyolultsággal járó kompromisszummal.
Jump Consistent Hash
2007-ben a Google két mérnöke publikálta a jump consistent hash-et. A gyűrű alapú algoritmushoz képest ez a megvalósítás “nem igényel tárolást, gyorsabb, és jobb munkát végez a kulcstér egyenletes elosztásában a vödrök között, valamint a munkaterhelés egyenletes elosztásában, amikor a vödrök száma változik”. Másképp fogalmazva, javítja a munkaterhelés elosztását a csomópontok között (egy bucket ugyanaz a fogalom, mint egy csomópont) memóriaterhelés nélkül.
Itt az algoritmus C++ nyelven (7 sornyi kód 🤯):
A gyűrűs konzisztens hash esetén 1000 virtuális csomóponttal a standard eltérés körülbelül 3,2% volt. Az ugráskonzisztens hash-ban már nincs szükségünk a virtuális csomópontok fogalmára. Ennek ellenére a standard eltérés továbbra is kevesebb, mint 0,0000001%.
Egy korlátozás azonban van. A csomópontokat sorszámozni kell. Ha van egy listánk a foo, bar és baz szerverekből, akkor nem tudjuk például a bar-öt eltávolítani. Mégis, ha beállítunk egy adattárolót, akkor alkalmazhatjuk az algoritmust, hogy a shard indexet a shardok teljes száma alapján kapjuk meg. Ezért a jump consistent hash hasznos lehet a shardinggal összefüggésben, de a terheléselosztással nem.
Mi a Perfect Consistent Hashing algoritmus?
Mivel már van némi tapasztalatunk a konzisztens hasheléssel kapcsolatban, lépjünk egy kicsit hátrébb, és nézzük meg, mi lenne a tökéletes algoritmus:
- A kulcsoknak átlagosan csak 1/n százalékát kellene átképezni, ahol n a csomópontok száma.
- O(n) térbonyolultságú, ahol n a csomópontok száma.
- A O(1) időbonyolultság egy csomópont beszúrásakor/eltávolításakor és egy kulcskereséskor.
- Minimális szórás annak biztosítására, hogy egy csomópont ne legyen túlterhelt egy másikhoz képest.
- Ez lehetővé tenné egy súly hozzárendelését egy csomóponthoz, hogy megbirkózzon a különböző csomópontméretekkel.
- Ez lehetővé tenné tetszőleges (nem sorszámozott) csomópontok elnevezését, hogy támogassa mind a terheléselosztást, mind a shardingot.
Ez az algoritmus sajnos nem létezik. A látottak alapján:
- A Rendezvousnak lineáris időbonyolultsága van keresésenként.
- A gyűrűs konzisztens hash-nak gyenge minimális standard eltérése van a virtuális csomópontok koncepciója nélkül. Virtuális csomópontokkal a térbonyolultság O(n*v), ahol n a csomópontok száma és v a virtuális csomópontok száma csomópontonként.
- A Jump consistent hash nem rendelkezik állandó időbonyolultsággal, és nem támogatja a tetszőleges csomópontok nevét.
A téma még mindig nyitott, és vannak újabb tanulmányok, amelyeket érdemes megnézni. Például a 2005-ben kiadott multi-probe konzisztens hash. Ez O(1) térbeli komplexitást támogat. Mégis, ε standard eltérés eléréséhez O(1/ε) időt igényel keresésenként. Ha például 0,5%-nál kisebb szórást akarunk elérni, akkor a kulcsot körülbelül 20-szor kell hashelni. Ezért minimális szórást érhetünk el, de nagyobb keresési időbonyolultsággal járó erőfeszítések árán.

Amint a bevezetőben említettük, a konzisztens hashing algoritmusok általánossá váltak. Ma már számtalan rendszerben használják, mint például a MongoDB, Cassandra, Riak, Akka stb. legyen szó a terhelés kiegyenlítéséről vagy az adatok elosztásáról. Azonban, mint az informatikában gyakran, minden megoldásnak vannak kompromisszumai.
Apropó kompromisszumok, ha szükséged van a folytatásra, akkor érdemes megnézned Damian Gryski kiváló bejegyzését:
Leave a Reply