Helmholtz-rezonancia
- A Helmholtz-rezonancia elemzése
- Rezonancia, impedancia, fázis- és frekvenciafüggés
- A hosszal kapcsolatos komplikációk
- Helmholtz-rezonanciák és gitárok
A Helmholtz-rezonancia elemzése
Most pedig térjünk át a kvantitásra: Először is tegyük fel, hogy a keletkező hang hullámhossza jóval hosszabb, mint a rezonátor méretei. Az oldal tetején látható animációban szereplő palackok esetében a hullámhossz 180, illetve 74 cm, tehát ez a közelítés elég jó, de érdemes ellenőrizni, amikor valamit Helmholtz-oszcillátorként kezdünk leírni. Ennek a közelítésnek az a következménye, hogy elhanyagolhatjuk a tartály térfogatán belüli nyomásváltozásokat: a nyomásrezgésnek a tartályon belül mindenhol ugyanaz lesz a fázisa.
Legyen a nyakban lévő levegő effektív hossza L és keresztmetszeti területe S. Tömege ekkor a levegő sűrűségének ρ-szerese SL. (Az effektív hosszal kapcsolatos néhány bonyodalmat az oldal végén tárgyaljuk.) Ha ez a levegő “dugó” egy kis x távolságot ereszkedik le a palackba, akkor összenyomja az edényben lévő levegőt, így a korábban V térfogatot elfoglaló levegőnek most V – Sx térfogata van. Következésképpen ennek a levegőnek a nyomása a PA légköri nyomásról PA + p magasabb értékre emelkedik.
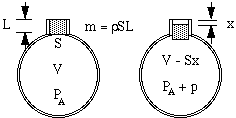
Most azt gondolhatnánk, hogy a nyomásnövekedés egyszerűen arányos a térfogatcsökkenéssel. Ez akkor lenne így, ha a tömörítés olyan lassan történne, hogy a hőmérséklet nem változna. A hangot keltő rezgéseknél azonban a változások gyorsak, így a hőmérséklet a tömörítéskor megemelkedik, ami nagyobb nyomásváltozást eredményez. Technikailag ezek adiabatikusak, ami azt jelenti, hogy a hőnek nincs ideje mozogni, és a kapott egyenletben szerepel egy γ konstans, a fajhő hányadosa, amely a levegő esetében körülbelül 1,4-es. (Ezt egy függelékben magyarázzuk.) Ennek eredményeképpen a ΔV kis térfogatváltozás által előidézett p nyomásváltozás csak
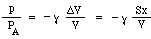
Most az m tömeget a nyak felső és alsó része közötti nyomáskülönbség, azaz egy pS nettó erő mozgatja, így az a gyorsulásra Newton törvényét írjuk fel:
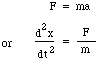
F és m helyettesítésével megkapjuk: 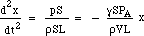
Tehát a visszaállító erő arányos az elmozdulással. Ez a feltétele az egyszerű harmonikus mozgásnak, amelynek frekvenciája az arányossági állandó négyzetgyökének 1/2π-szerese, tehát
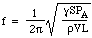
Most a hang c sebességét a levegőben a sűrűség, a nyomás és a fajhők aránya határozza meg, tehát felírhatjuk:
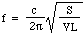
Tegyünk be néhány számot: egy 1 literes palack esetében, amelynek S = 3 négyzetcentimétere és L = 5 centimétere van, a frekvencia 130 Hz, ami körülbelül a középső C alatti C. (Lásd a jegyzeteket.) Tehát a hullámhossz 2,6 méter, ami sokkal nagyobb, mint a palack. Ez utólag igazolja a levezetés elején tett feltételezést.
Rezonancia, impedancia, fázis- és frekvenciafüggés
Ez a rész önmagában is olvasható, de ha részletesebb háttérre vágysz, lásd az Oszcillációk, a Kényszerrezgések és az Akusztikai megfelelőség, tehetetlenség és impedancia című fejezeteket.
Kanyarodjunk vissza a mechanikai ábrázoláshoz, és nézzük meg a Helmholtz-rezonátort kívülről, ahogy az első vázlatképen látható: F rezgőerővel, f frekvenciával toljuk az m tömeget (a rezonátor nyakában lévő levegőt), amely a k rugóállandójú rugón (a zárt levegőn) nyugszik, amelynek másik vége rögzített (a rezonátorban lévő levegő nem tud kiszökni). Valószerűtlenül elhanyagoljuk a gravitációt és a súrlódást (egyelőre).
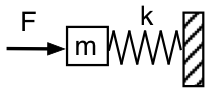
A tömeg gyorsításához szükséges erő arányos a gyorsulással, tehát arányos f2-vel. Megfelelően alacsony frekvencián a tömeg gyorsításához szükséges erő elhanyagolható, tehát F-nek csak a rugót kell összenyomnia és kinyújtania. Ebben a határértékben tehát az alkalmazott erő F = +kx. (A rugóerő -kx.) A rendszer mechanikai impedanciája ezen az alacsony frekvencián engedékeny vagy rugószerű. Akusztikailag úgy néz ki, mint egy akusztikus engedékenység: a nyakban lévő légtömeget nyomjuk és a rezonátorban lévő levegőt összenyomjuk. Az alkalmazott F erő jobbra fázisban van a jobbra mért x-szel, tehát 90°-kal elmarad a sebességtől, és az alkalmazott nyomás 90°-kal elmarad a rezonátorba irányuló akusztikus áramlástól.
Memlékezzünk arra, hogy f2 a gyorsulás függvénye. Tehát kellően nagy frekvencián a rugóerő elhanyagolható a tömeget gyorsító erőhöz képest. Tehát F fázisban van a gyorsulással, ami 90°-kal a sebesség elé helyezi. Akusztikailag az alkalmazott nyomás 90°-kal megelőzi a rezonátorba irányuló akusztikus áramlást. Ez egy mechanikai vagy akusztikai tehetetlenség.
A rezonanciafrekvencián (még mindig a fenti vázlatról beszélünk) az amplitúdó nagyon kis erő mellett is nagy lehet. Tehát rezonanciánál az impedancia nagyon alacsony, ha a tömegre kívülről ható erőt nézzük (a fenti ábra). A rezonanciánál maximális áramlás van a rezonátorba és a rezonátorból kifelé.
Most nézzük meg, mi történik, ha a rezonátor belsejében (a nyaktól távolodva) lévő nyomást nézzük. Itt a rugóra ható erőt nézzük, így a mechanikai analógunk úgy néz ki, mint ez a vázlat.
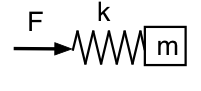
Ezúttal az alacsony frekvencia azt jelenti, hogy az erő adott amplitúdó mellett kicsi lehet: a rugó és a tömeg egy tömegként mozog, és a rendszer ezúttal alacsony frekvencián inertnek tűnik. Nagy frekvencián a tömeg alig mozog, és a rendszer rugószerű vagy engedékeny. A fázisviszonyok tehát ellentétesek a korábbiakkal: kis f-nél a p 90°-kal megelőzi az U-t; nagy f-nél a p 90°-kal lemarad az U-tól.
A hatásos hosszal kapcsolatos számítások
Az első ábra ezen az oldalon úgy rajzolja meg a levegő “dugóját”, mintha az egy henger lenne, amely szépen végződik a palack nyakának mindkét végén. Ez túlságosan leegyszerűsített. A gyakorlatban a nyakban lévő levegővel együtt mozog egy külső és egy belső extra térfogat is – ahogy azt a fenti animáció is sugallja. A nyak geometriai hosszához hozzáadandó extra hossz jellemzően (és nagyon közelítőleg) 0,6-szoros sugarú a külső végén, és egy sugár a belső végén).
|
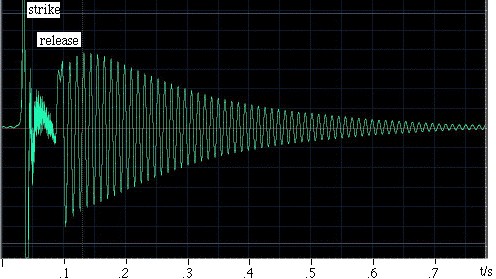
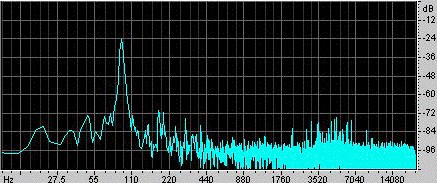
Egy példa. Ra Inta készítette ezt a példát. Vett egy 0,00292 m3 térfogatú gömb alakú Helmholtz-rezonátort, amelynek hengeres nyaka 0,080 m hosszú és 0,00083 m2 keresztmetszetű. A gerjesztéshez a tenyerével megütötte, majd elengedte. A rezonátor belsejében lévő mikrofon rögzíti a hangot, amely a bal oldali oszcillogramon látható. Látható, hogy a kéz inkább kevesebb mint 0,1 s-ig zárja le a rezonátort, és hogy ez idő alatt a rezgések gyengébbek és viszonylag nagy frekvenciájúak. Amint a kezet elengedjük, oszcilláció jön létre, amely fokozatosan elhal, mivel a viszkózus és turbulens ellenállás, valamint a hangsugárzás révén energiát veszít. A közelebbi vizsgálat azt mutatja, hogy a frekvencia kissé emelkedik, ahogy a kéz eltávolodik a nyitott végtől, mert ez a kéz korlátozza a sugárzáshoz rendelkezésre álló térszöget, és így növeli a véghatást (vagy végkorrekciót). A nyak hossza megnő egy elfalazott és egy elfalazatlan véghatással, így az effektív hossza 0,105 m. 343 m/s hangsebességgel számolva a fenti kifejezés 90 Hz rezonanciafrekvenciát ad. |
|
Helmholtz-rezonanciák és gitárok
* Fentebb azt mondtam, hogy a gitár testében lévő levegő majdnem úgy viselkedik, mint egy Helmholtz-oszcillátor. Ez az eset azért bonyolult, mert a test egy kicsit megduzzadhat, amikor a benne lévő levegő nyomása megemelkedik – és azért is, mert a gitár hanglyukában “lévő” levegő geometriája nehezebben szemléltethető, mint egy palack nyakában lévőé. A gitártest esetében ugyanis a levegő dugójának hossza nagyjából megegyezik a mindössze néhány mm vastagságú “cső” végén lévő két “véghatással”. A véghatások azonban a lyuk sugarához viszonyítva és ahhoz hasonló méretűek, így a levegő tömege jelentős. Egy végtelen, sík terelőlapra nyíló hengeres cső véghatásának hossza a cső sugarának 0,85-szöröse. Bár a gitár hangfala nem végtelen, hasonló véghatás várható, így a levegő “dugójának” tényleges hossza körülbelül a lyuk sugarának 1,7-szerese. (Egyes gyártók ezt úgy növelik meg, hogy a hanglyuk alá egy rövid, azonos sugarú csövet rögzítenek).
Néhányan írtak arról, hogy mekkora legyen a hanglyuk egy adott hangszer esetében. Nos, a fenti egyenlet segítségével elkezdhetjük megválaszolni ezt a kérdést. Fontos azonban a test duzzadása. Ez ugyanis a levegő “rugózását” meglehetősen lágyabbá teszi, és így csökkenti a frekvenciát. A tisztán Helmholtz-rezonancia a test térfogatának állandó értéken tartásával vizsgálható. Ennek mérésekor gyakori gyakorlat, hogy a gitárt homokba temetjük, hogy megakadályozzuk a test duzzadását vagy “légzését”. A gitárokat azonban általában nem ebben a helyzetben játsszák. Így a Helmholtz-számítás túlbecsüli a rezonancia frekvenciáját egy valódi, rugalmas test esetében.
Tegyük fel, hogy a hanglyuk kör alakú, r sugarú, tehát S = πr2, és L = 1,7r a fentiek szerint. Ha behelyettesítjük a Helmholtz-frekvencia egyenletébe, c = 340 m/s használatával, azt kapjuk:
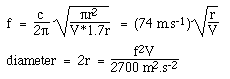
Vegyük észre, hogy szabványos SI-egységeket használunk: a hangsebességet méterben és másodpercben használtuk, tehát a térfogatot köbméterben, a frekvenciát pedig Hertzben kell megadnunk, hogy a választ méterben adjuk meg.
Bonyolultabb a helyzet, ha a hanglyukak nem kör alakúak, mert a végeredmény nem egyenlő egy azonos területű körrel. John McLennan doktorandusz és lantművész épp most írja meg néhány mérésről szóló beszámolóját erről, amit hamarosan közzéteszünk itt.
A gitár és hegedű családba tartozó hangszereken a Helmholtz (plusz test) rezonancia gyakran a második legmélyebb húr frekvenciájához közel vagy kicsit alatta van, D körül a hegedűn vagy G-A körül a gitáron. A Helmholtz-frekvenciát jelentősen csökkentheted vagy eltolhatod, ha a lyuk egészét vagy egy részét egy megfelelően formázott, merev kartondarabbal feded le. Ha ezután a rezonancia közelében játszunk egy hangot, majd a kartont úgy csúsztatjuk, hogy az felváltva takarja és felfedi a lyukat, tisztán hallani fogjuk a rezonancia hatását.
A 0,85r hatás ésszerű? Ra Inta, aki nálunk doktorált gitárakusztikából, egy érdekes demonstrációt javasol:
Nedvesítsd a húrokat a gitárodon, hogy ne rezegjenek (pl. egy zsebkendő a húrok és a fogólap közé). Tartsa az egyik tenyerét a hanglyuk fölé, és közel a hanglyukhoz. A másik kezed egyik ujjával üss élesen a hangfalat a hanglyuk közelében és az 1. húr közelében. A tenyerén érezni fogja a levegő lüktetését. Az ujjad ütése benyomja a hangfalat, és némi levegőt présel ki a testből. Most mozgassa a kezét fokozatosan távolabb a hanglyuktól, és folytassa a kopogtatást az ujjával. Mikor szűnik meg érezni a levegő mozgását? Ez nagyjából megadja a “véghatás” hosszát a hanglyuk esetében.
A Helmholtz-rezonancia hangolása
John McLennan, e laboratórium PhD-hallgatójának publikációi között van egy cikk, amelyben a hangsebesség változtatásával variálja a Helmholtz-rezonanciát.
- McLennan, J.E. (2003) “A0 és A1 vizsgálatok a hegedűn CO2, He és levegő/hélium keverékekkel”. Acustica, 89, 176-180.
Néhány képet a történelmi Helmholtz-rezonátorokról Thomas B. Greenslade (Kenyon College, Ohio) bocsátott rendelkezésre.
Leave a Reply