Green-féle függvény

általában véve, a Green-függvény egy integrálmag, amely számos differenciálegyenlet-családból származó differenciálegyenletek megoldására használható, beleértve az egyszerűbb példákat, mint például a közönséges differenciálegyenletek kezdeti vagy peremértékfeltételekkel, valamint a nehezebb példákat, mint például az inhomogén parciális differenciálegyenletek (PDE) peremfeltételekkel. A számos okból fontos Green-függvények lehetővé teszik egy erőforráshoz vagy egy pontba koncentrált töltéshez kapcsolódó hatások szemléletes értelmezését (Qin 2014), így különösen hasznosak az alkalmazott matematika területein. Különösen a Green-funkciók módszereit széles körben használják pl, fizikában és a mérnöki tudományokban.

Pontosabban, adott egy lineáris differenciáloperátor , amely valamely euklideszi tér részhalmaza feletti eloszlások gyűjteményére hat, egy Green-függvény az Omega”> pontnak megfelelő a

(1)

ahol a deltafüggvényt jelöli. Egy ilyen függvény definiálásának motivációja széleskörű, de a fenti azonosságot megszorozva egy függvénnyel és a tekintetében integrálva

(2)

A jobb oldal a deltafüggvény tulajdonságai miatt pusztán -re redukálódik, és mivel egy lineáris operátor, amely csak -re hat és nem -re, a bal oldalt átírhatjuk

(3)

Ez a redukció különösen hasznos, ha alakú differenciálegyenletek

(4)

ahol a fenti aritmetika igazolja, hogy

(5)

és amiből következik, hogy a sajátos integrál alakja

(6)

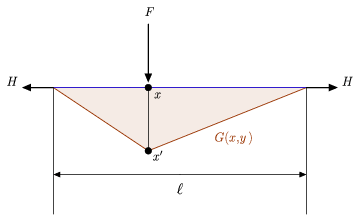
A fenti ábra szemlélteti mind a Green-funkció intuitív fizikai értelmezését, mind pedig egy viszonylag egyszerű kapcsolódó differenciálegyenletet, amellyel a fenti definíció összehasonlítható (Hartmann 2013). Konkrétan egy feszes, hosszúságú, két fal közé függesztett kötelet mutat, amelyet a két végére ható azonos vízszintes erő , valamint a kötél valamely belső pontján elhelyezett oldalirányú terhelés tart a helyén. Legyen az elhajló kötél pontjának megfelelő pont, tegyük fel, hogy a lefelé ható erő állandó, mondjuk , és jelölje a kötél elhajlását. Ennek a fizikai rendszernek megfelel a differenciálegyenlet

(7)

for azzal , egy olyan rendszer, amelynek egyszerűsége lehetővé teszi, hogy mind a megoldását , mind a Green-függvényét explicit módon írjuk fel:

(8)

és

(9)

különösen. Amint a fenti ábrán látható, az elmozdult kötél a fenti által megadott darabosan lineáris alakú, így megerősítve azt az állítást, hogy az ehhez a rendszerhez tartozó Green-függvény erő kifejtésének megfelelő vízszintes kötél hatását reprezentálja.

Az argumentumpárral rendelkező Green-függvényt néha kétpontos Green-függvénynek nevezik. Ez ellentétben áll a többpontos Green-függvényekkel, amelyek különösen fontosak a soktest-elmélet területén.

A fenti definíció szerinti kétpontos függvény elemi példájaként tekintsük azt a problémát, hogy meghatározzuk a potenciált, amelyet egy olyan töltéseloszlás generál, amelynek töltéssűrűsége , ahol a Poisson-egyenlet és a Coulomb-törvény alkalmazása az egyes töltéselemek által pontban létrehozott potenciálra

(10)

ami érvényes, bizonyos feltételek mellett abban a tartományban, ahol . Mivel a jobb oldalt egy integráloperátornak tekinthetjük, amely -t -re alakítja, ezt a megoldást átírhatjuk egy Green-függvény , amelynek alakja

(11)

mivel a megoldás átírható:

(12)

(Arfken 2012).

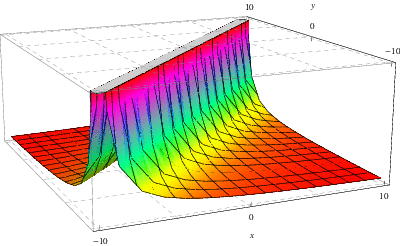
A fenti ábrán a fent tárgyalt – egyenlet megoldásához tartozó Green-függvény látható, ahol itt, és , illetve , a -, illetve – tengelyen van ábrázolva.

A különböző differenciálegyenleteknek megfelelő Green-függvények némileg átfogó listáját Kevin Cole tartja fenn az interneten (Cole 2000).

A Green-függvényekről írt irodalom sokasága miatt számos különböző jelölés és definíció jelenhet meg, amelyek közül néhány tematikusan eltér a fentiektől, de általában nem befolyásolja az eredmények fontos tulajdonságait. Mint a fenti példa is mutatja, egyes szerzők például a és változókat inkább és vektorokkal jelölik, hogy hangsúlyozzák, hogy ezek elemei valamilyen esetén, amely lehet nagyobb, mint 1 (Arfken 1985). Viszonylag gyakori az is, hogy a definíciót negatív előjellel látjuk, így az a függvény, amelyre

(13)

de mivel ez a tisztán fizikai megfontolás nincs hatással a mögöttes matematikára, ezt a szempontot általában figyelmen kívül hagyják. Számos más jelölés is ismert a Green-függvényre, ezek közül néhány a kisbetűs használata a helyett (Stakgold 1979), valamint a vessző helyett egy függőleges vonal szerepeltetése, pl, (Duffy 2001).

Más esetekben a szakirodalom olyan definíciókat mutat be, amelyek szorosan kapcsolódnak a kontextushoz, amelyben bemutatásra kerülnek. Például egyes szerzők úgy definiálják a Green-függvényeket, hogy azok olyan függvények, amelyek bizonyos feltételeknek megfelelnek, pl. létezés egy speciális típusú tartományon, társulás egy nagyon speciális differenciáloperátorral , vagy peremfeltételek egy pontos halmazának kielégítése. Az egyik leggyakoribb ilyen példa megtalálható pl. a jegyzetekben, Speck, ahol egy Green-függvényt úgy definiálnak, hogy az Omega×Omega(x,s) pontjaira (x,s) és minden olyan pontra, amely a határán fekszik (Speck 2011). Ez a konkrét definíció egy általánosított Poisson-egyenlet megoldásának megfelelő integrálmagot mutat be, és ezért nyilvánvaló korlátokba ütközne, ha általánosabb környezetre adaptálnánk. Másrészt az ilyen példák nem nélkülözik az előnyöket. A fenti általánosított Poisson-példa esetében például minden ilyen Green-függvény felosztható úgy, hogy

(14)

ahol és a szabályos Laplacián (Hartman 2013). Ilyen helyzetekben a mögöttes differenciálegyenlet fundamentális megoldásának, pedig szabályos megoldásának nevezzük; mint ilyeneket, és néha fundamentális, illetve szabályos részének nevezzük.

Az általános Green-függvény több alapvető tulajdonsága azonnal (vagy majdnem) következik a definíciójából, és átvihető minden egyedi példányra. Például, ha az operátor kernele nem triviális, akkor egyetlen operátorhoz több Green-funkció is kapcsolódhat; ennek következtében óvatosságot kell tanúsítanunk, amikor “a” Green-funkcióra hivatkozunk. A Green-függvények két argumentumukban adjungált szimmetriát teljesítenek, így

(15)

ahol itt a

(16)

Itt a adjungáltja. Ennek a ténynek az egyik közvetlen következménye, hogy a önadjungált operátorok esetében szimmetrikus:

(17)

Ezt az azonosságot gyakran reciprocitás elvének nevezik, és fizikai értelemben azt mondja ki, hogy a pontban egy pontban lévő egységnyi forrás által okozott válasz megegyezik a pontban egy pontban lévő egységnyi erő által okozott válasszal (Stakgold 1979).

Minden Green-függvény alapvető tulajdonsága, hogy módot ad egy tetszőleges differenciálegyenlet megoldásának valamilyen forrástényezőre adott válaszának leírására bizonyos számú peremfeltétel jelenlétében (Arfken et al. 2012). Egyes szerzők szerint a Green-funkció nagyjából analóg szerepet tölt be a parciális differenciálegyenletek elméletében, mint a Fourier-sorok a közönséges differenciálegyenletek megoldásában (Mikula és Kos 2006).

Az elvontabb forgatókönyvek esetében számos olyan fogalom létezik, amelyek a Green-funkció fogalmának kontextus-specifikus analógjaiként szolgálnak. Például a funkcionálanalízisben gyakran hasznos egy úgynevezett általánosított Green-funkciót figyelembe venni, amely számos analóg tulajdonsággal rendelkezik, ha absztrakt módon függvények helyett függvények ellenében integráljuk. Valójában az ilyen általánosítások az elméleti PDE-analízis egy teljesen analóg ágát eredményezték, és maguk is számos kutatás középpontjában állnak.