Articles /

Gram-Schmidt-eljárás

by Marco Taboga, PhD

A Gram-Schmidt-eljárás (vagy eljárás) olyan műveletsorozat, amely lineárisan független vektorok halmazát olyan ortonormális vektorok halmazává alakítja át, amelyek ugyanazt a teret fedik le, mint az eredeti halmaz.

Tartalomjegyzék

Elöljárások

Tekintsünk át néhány fogalmat, amelyek elengedhetetlenek a Gram-Schmidt-eljárás megértéséhez.

Ne feledjük, hogy két vektort $r$ és $s$ akkor és csak akkor mondjuk ortogonálisnak, ha belső szorzatuk egyenlő nullával, azaz

Belső szorzat birtokában a $s$ vektor normáját (hosszát) a következőképpen határozhatjuk meg:

Egy vektorhalmazt akkor és csak akkor nevezünk ortonormálisnak, ha az elemei egységnyi normával rendelkeznek és ortogonálisak egymásra. Más szóval, egy K vektorokból álló halmaz akkor és csak akkor ortonormális, ha

Bizonyítottuk, hogy egy ortonormális halmaz vektorai lineárisan függetlenek.

Ha egy vektortér bázisa egyben ortonormális halmaz is, akkor ortonormális bázisnak nevezzük.

Projekciók ortonormális halmazokra

A Gram-Schmidt-eljárásban ismételten használjuk a következő tételt, amely megmutatja, hogy minden vektor két részre bontható: 1) egy ortonormális halmazra való vetülete és 2) egy maradék, amely ortogonális az adott ortonormális halmazra.

Tétel Legyen $S$ egy belső szorzóval ellátott vektortér. Legyen egy ortonormális halmaz. Bármely $sin S$ esetén van ahol $arepsilon _{S}$ ortogonális $u_{k}$ bármely $k=1,ldots ,K esetén.$

Bizonyítás

DefiniáljukEzután minden $j=1,ldots ,K$ esetében azt kell, hogyhol: $keret{A}$ és $keret{B}$ lépésekben felhasználtuk azt a tényt, hogy a belső szorzat lineáris az első argumentumában; a $rame{C}$ lépésben azt a tényt használtuk, hogy ha $keq j$, mivel ortonormális halmazzal van dolgunk; a $rame{D}$ lépésben azt a tényt használtuk, hogy a $u_{j}$ normája egyenlő 1-gyel. Ezért a $arepsilon _{S}$ a fenti definíció szerint ortogonális az ortonormális halmaz minden elemére, ami bizonyítja a tételt.

A kifejezést $s$ lineáris vetületének nevezzük a ortonormális halmazra, míg a $arepsilon _{S}$ kifejezést a lineáris vetület maradékának.

Normálás

Egy másik talán nyilvánvaló tény, amit a Gram-Schmidt-eljárásban többször is használni fogunk, hogy ha bármelyik nem nulla vektort vesszük, és elosztjuk a normájával, akkor az osztás eredménye egy új vektor, amelynek egységnormája van.

Más szóval, ha , akkor a norma határozottsági tulajdonsága alapján azt kapjuk, hogy

Ennek következtében definiálhatjukés a norma pozitivitása és abszolút homogenitása alapján a normát, van

Az eljárás áttekintése

Most, hogy tudjuk, hogyan normálhatunk egy vektort, és hogyan bonthatjuk szét egy ortonormális halmazra való vetítésre és egy maradékra, készen állunk a Gram-Schmidt-eljárás magyarázatára.

Az eljárásról áttekintést adunk, majd formálisan, tételként fogjuk kifejezni, és a tétel bizonyításában minden technikai részletre kitérünk.

Íme az áttekintés.

Adott egy lineárisan független vektorok halmaza .

A folyamat megkezdéséhez normalizáljuk az első vektort, azaz definiáljuk

A második lépésben $s_{2}$ vetítjük $u_{1}$:-ra, ahol $arepsilon _{2}$ a vetítés maradékát.

Ezután normalizáljuk a maradékot:

Később bebizonyítjuk, hogy (így a normalizálás elvégezhető), mert a kiindulási vektorok lineárisan függetlenek.

Az így kapott két vektor $u_{1}$ és $u_{2}$ ortonormális.

Harmadik lépésben $s_{3}$ vetítjük $u_{1}$ és $u_{2}$: és kiszámítjuk a vetítés $arepsilon _{3}$ maradékát.

Ezután normalizáljuk:

Így folytatjuk, amíg megkapjuk az utolsó normalizált maradékot $u_{K} $.

A folyamat végén a vektorok ortonormális halmazt alkotnak, mert:

  1. normalizálás eredménye, és ennek következtében egységnyi normájuk van;

  2. minden $u_{k}$ maradékból kapjuk, amely rendelkezik azzal a tulajdonsággal, hogy -re ortogonális.

Az áttekintés teljessé tételéhez emlékezzünk arra, hogy a lineáris tartománya az összes olyan vektor halmaza, amely lineáris kombinációjaként írható fel; eztvel jelöljük, és ez egy lineáris tér.

Mivel a vektorok lineárisan független kombinációi, minden olyan vektor, amely lineáris kombinációjaként írható fel, felírható lineáris kombinációjaként is. Ezért a két vektorhalmaz terjedelme egybeesik:

Formális állítás

A Gram-Schmidt-eljárást itt tételként formalizáljuk, amelynek bizonyítása tartalmazza az eljárás minden technikai részletét.

Tétel Legyen $S$ egy belső szorzóval ellátott vektortér. Legyenek lineárisan független vektorok. Ekkor létezik olyan ortonormális vektorok halmaza, hogyminden $kleq K$ esetén.

Bizonyítás

A bizonyítás indukcióval történik: először azt bizonyítjuk, hogy a tétel igaz $k=1$-re, majd azt, hogy egy általános k-ra igaz, ha $k-1$-re igaz. Ha $k=1$, akkor a vektornak egységnormája van, és önmagában ortonormális halmazt alkot: nincs más vektor, tehát az ortogonalitás feltétele triviálisan teljesül. Ahalmaz $s_{1}$ összes olyan skaláris többszöröseinek halmaza, amelyek egyben $u_{1}$ skaláris többszörösei (és fordítva). Ezért Most tegyük fel, hogy a tétel igaz $k-1$ esetében. Akkor $s_{k}$ vetíthetjük :-re, ahol a $arepsilon _{k}$ maradék -re ortogonális. Tegyük fel, hogy $arepsilon _{k}=0$<. Akkor,Mivel a feltételezés szerint minden $jleq k-1$ esetén minden $jleq k-1$ esetén, ahol $lpha _{jl}$ skalárok. Ezért,Más szavakkal, az a feltételezés, hogy $arepsilon _{k}=0$ ahhoz a következtetéshez vezet, hogy $s_{k}$ lineáris kombinációja . Ez azonban lehetetlen, mert a tétel egyik feltételezése az, hogy lineárisan független. Következésképpen annak kell lennie, hogy . Ezért normalizálhatjuk a maradékot, és definiálhatjuk avektort, amelynek egységnyi normája van. Azt már tudjuk, hogy $arepsilon _{k}$ ortogonális -re. Ebből következik, hogy $u_{k}$ is ortogonális -re. Tehát egy ortonormális halmaz. Most vegyünk bármilyen $sin S$ vektort, amely felírható ként, ahol skalárok. Mivel a feltételezés szerint megvan, hogy a (2) egyenlet is felírható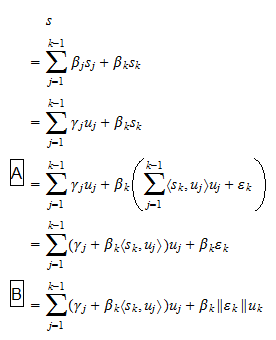ahol skalárok, és: a $ráma{A}$ lépésben az (1) egyenletet használtuk; a $ráma{B}$ lépésben a $u_{k}$ definícióját használtuk. Így bebizonyítottuk, hogy minden olyan vektor, amely lineáris kombinációjaként írható fel, lineáris kombinációjaként is felírható. A (3) feltételezés lehetővé teszi, hogy a fordítottját teljesen analóg módon bizonyítsuk: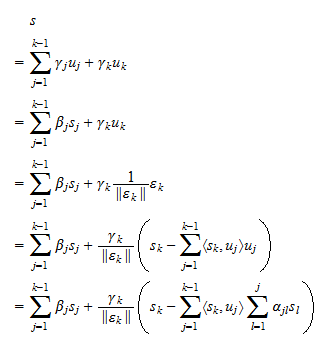Más szóval, minden lineáris kombinációja egyben lineáris kombinációja is. Ez bizonyítja, hogy és lezárja a bizonyítást.

Minden belső szorzatú térnek van ortonormális bázisa

A következő tétel a Gram-Schmidt-eljárás egy fontos következményét mutatja be.

Tétel Legyen $S$ egy belső szorzattal ellátott vektortér. Ha $S$$ véges dimenziójú, akkor létezik ortonormális bázis a $S$$ számára.

Bizonyítás

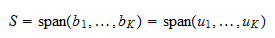Mivel $S$$ véges dimenziós, létezik legalább egy bázis $S$ számára, amely K vektorokból áll. A bázisra alkalmazhatjuk a Gram-Schmidt eljárást, és kapunk egy ortonormális halmazt. Mivel egy bázis, ezért az $S$-et átfogja. Ezért Ezért a $S$ ortonormális bázisa.

Megoldott feladatok

Az alábbiakban néhány feladatot találunk magyarázott megoldásokkal.

GYakorlat 1

Tekintsük az $S$$ teret, amely az összes $3szor 1$ valós bejegyzésű vektorból és a belső szorzatból áll, ahol $r,sin S$ és $s^{op }$ a $s$ transzponáltja. Definiáljuk a vektor

normalizálását $s$.

megoldás

A $s$ normájaEzért, $s$ normája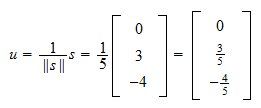

2. feladat

Tekintsük az összes $2szer 1$ valós bejegyzésű vektorok $S$ terét és a belső szorzatotahol $r,sin S$ . Tekintsük a két lineárisan független vektort

A Gram-Schmidt eljárás segítségével transzformáljuk őket ortonormális halmazzá.

megoldás

A $s_{1}$ normája Ezért, az első ortonormális vektorA $s_{2}$ és $u_{1}$ belső szorzata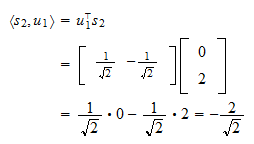A $s_{2}$ vetülete $u_{1}$-re 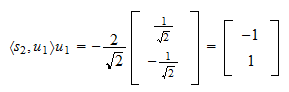A vetület maradéka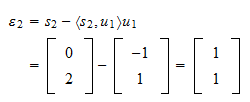A maradvány normájaés a normalizált maradványÍgy, a keresett ortonormális halmaz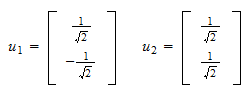

How to cite

Please cite as:

Taboga, Marco (2017). “Gram-Schmidt-folyamat”, Előadások a mátrixalgebráról. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply