Gibbs mintavételezés

Mint más MCMC módszerek, a Gibbs-mintavevő egy Markov-láncot épít fel, amelynek értékei egy céleloszlás felé konvergálnak. A Gibbs-mintavételezés tulajdonképpen a Metropolis-Hastings algoritmus egy speciális esete, amelyben a javaslatokat mindig elfogadják.

Elmagyarázzuk, tegyük fel, hogy egy többváltozós valószínűségi eloszlásból szeretnénk mintát venni.

Megjegyzés: A többváltozós valószínűségi eloszlás több változó függvénye (pl. 2 dimenziós normális eloszlás).

Ez utóbbiból közvetlenül nem tudunk mintát venni. Viszont valamilyen matematikai kényelem vagy talán csak puszta szerencse folytán történetesen ismerjük a feltételes valószínűségeket.

Itt jön a képbe a Gibbs-féle mintavételezés. A Gibbs-mintavételezés akkor alkalmazható, ha az együttes eloszlás nem ismert explicit módon, vagy nehéz közvetlenül mintát venni belőle, de az egyes változók feltételes eloszlása ismert, és könnyebb belőle mintát venni.

Azzal kezdjük, hogy kiválasztunk egy kezdeti értéket az X & Y véletlen változóknak. Ezután X feltételes valószínűségi eloszlásából veszünk mintát, adott Y = Y⁰, amelyet p(X|Y⁰) jelölünk. A következő lépésben mintavételezzük Y új értékét az X¹ függvényében, amelyet az imént kiszámítottunk. Az eljárást további n – 1 iteráción keresztül megismételjük, felváltva húzunk új mintát az X feltételes valószínűségeloszlásából és az Y feltételes valószínűségeloszlásából, a másik véletlen változó aktuális értéke mellett.

Nézzünk egy példát. Tegyük fel, hogy a következő utólagos és feltételes valószínűségi eloszlásokkal rendelkezünk.

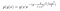
ahol g(y) tartalmazza azokat a feltételeket, amelyek nem tartalmazzák x-et, és g(x) tartalmazza azokat, amelyek nem függenek y-tól.

Nem ismerjük a C (normalizáló konstans) értékét. Ismerjük azonban a feltételes valószínűségeloszlásokat. Ezért Gibbs mintavételezéssel közelíthetjük az utólagos eloszlást.

Megjegyzés: A feltételes valószínűségek valójában normális eloszlások, és a következőképpen írhatók át:

Az előző egyenletek ismeretében folytassuk a Gibbs mintavételi algoritmus Pythonban történő implementálását. Kezdetnek importáljuk a következő könyvtárakat.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Meghatározzuk a poszterior eloszlás függvényét (feltételezzük, hogy C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Ezután ábrázoljuk a valószínűségi eloszlást.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Most megpróbáljuk a valószínűségi eloszlást Gibbs-mintavételezéssel becsülni. Mint korábban említettük, a feltételes valószínűségek normális eloszlások. Ezért mu és sigma értékekkel fejezhetjük ki őket.

A következő kódblokkban függvényeket definiálunk a mu és sigma értékekhez, inicializáljuk az X & Y véletlen változóinkat, és beállítjuk N-t (az iterációk számát).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Végiglépünk a Gibbs Sampling algoritmuson.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Végül ábrázoljuk az eredményeket.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Mint láthatjuk, a Gibbs Sampling algoritmus segítségével kapott valószínűségi eloszlás jól közelíti a céleloszlást.

Következtetés

A Gibbs-mintavételezés egy Monte Carlo Markov-lánc módszer, amely iteratív módon húz egy példányt az egyes változók eloszlásából, a többi változó aktuális értékének függvényében, hogy komplex közös eloszlásokat becsüljön. A Metropolis-Hastings algoritmussal ellentétben mindig elfogadjuk a javaslatot. Így a Gibbs-mintavételezés sokkal hatékonyabb lehet.