Friedman-teszt az SPSS Statisticsban
SPSS Statistics
SPSS Statistics Kimenet a Friedman-teszthez
Az SPSS Statistics két vagy három táblázatot generál, attól függően, hogy a Friedman-teszt futtatása mellett a leíró és/vagy kvartilisek generálását is kiválasztotta.
leíró statisztikai táblázat
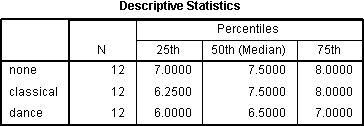
A leíró statisztikai táblázat akkor jön létre, ha a kvartilisek opciót választotta:
Published with written permission from SPSS Statistics, IBM Corporation.
Ez egy nagyon hasznos táblázat, mert felhasználható a leíró statisztikák bemutatására az eredmények részben az egyes időpontokra vagy feltételekre (a vizsgálati tervtől függően) a függő változóra vonatkozóan. Ezt a hasznosságot később a “Kimenetek jelentése” című részben mutatjuk be.
Rangok táblázat
A Rangok táblázat az egyes kapcsolódó csoportok átlagos rangsorát mutatja, ahogy az alábbiakban látható:

Published with written permission from SPSS Statistics, IBM Corporation.
A Friedman-teszt a kapcsolódó csoportok közötti átlagos rangsorokat hasonlítja össze, és jelzi, hogy a csoportok hogyan különböztek, ezért szerepel. Azonban nem valószínű, hogy ténylegesen ezeket az értékeket fogja közölni az eredmények részben, hanem valószínűleg az egyes kapcsolódó csoportok mediánértékét fogja közölni.
Tesztstatisztikai táblázat
A tesztstatisztikai táblázat tájékoztatja Önt a Friedman-teszt tényleges eredményéről, és arról, hogy volt-e összességében statisztikailag szignifikáns különbség a kapcsolódó csoportok átlagos rangsorai között. Az ebben az útmutatóban használt példa esetében a táblázat a következőképpen néz ki:

Published with written permission from SPSS Statistics, IBM Corporation.
A fenti táblázat megadja a tesztstatisztika (χ2) értékét (“Chi-square”), a szabadságfokokat (“df”) és a szignifikancia szintet (“Asymp. Sig.”), amire csak szükségünk van a Friedman-teszt eredményének közléséhez. Példánkból láthatjuk, hogy összességében statisztikailag szignifikáns különbség van a kapcsolódó csoportok átlagos rangsorai között. Fontos megjegyezni, hogy a Friedman-teszt egy omnibusz teszt, akárcsak parametrikus alternatívája; vagyis azt mondja meg, hogy vannak-e általános különbségek, de nem határozza meg pontosan, hogy konkrétan mely csoportok különböznek egymástól. Ehhez post hoc teszteket kell futtatnia, amelyeket a következő szakasz után tárgyalunk.
SPSS Statistics
A Friedman-teszt eredményének jelentése (post hoc tesztek nélkül)
A Friedman-teszt eredményét a következőképpen jelentheti:
- Általános
Az érzékelt erőfeszítésben statisztikailag szignifikáns különbség volt attól függően, hogy milyen típusú zenét hallgattak futás közben, χ2(2) = 7.600, p = 0,022.
Az egyes kapcsolódó csoportok mediánértékeit is megadhatná. Ebben a szakaszban azonban csak azt tudja, hogy valahol különbségek vannak a kapcsolódó csoportok között, de azt nem tudja, hogy pontosan hol vannak ezek a különbségek. Ne feledje azonban, hogy ha a Friedman-teszt eredménye nem volt statisztikailag szignifikáns, akkor nem szabad post hoc teszteket futtatnia.
Post Hoc tesztek
Azért, hogy megvizsgálja, hol vannak valójában a különbségek, külön Wilcoxon előjeles rangsor teszteket kell futtatnia a kapcsolódó csoportok különböző kombinációin. Ebben a példában tehát a következő kombinációkat hasonlítaná össze:
- None to Classical.
- None to Dance.
- Classical to Dance.
A Wilcoxon-tesztekből kapott eredményeken Bonferroni-korrekciót kell alkalmaznia, mivel többszörös összehasonlításokat végez, ami valószínűbbé teszi, hogy egy eredményt szignifikánsnak nyilvánít, amikor nem kellene (I. típusú hiba). Szerencsére a Bonferroni-korrekciót nagyon könnyű kiszámítani; egyszerűen vegye az eredetileg használt szignifikancia szintet (ebben az esetben 0,05), és ossza el a lefuttatott tesztek számával. Tehát ebben a példában az új szignifikancia-szint 0,05/3 = 0,017. Ez azt jelenti, hogy ha a p-érték nagyobb, mint 0,017, akkor nincs statisztikailag szignifikáns eredményünk.
Ezeket a teszteket lefuttatva (lásd a Wilcoxon signed-rank teszt útmutatóval) ennek a példának az eredményein, a következő eredményt kapjuk:

Published with written permission from SPSS Statistics, IBM Corporation.
Ez a táblázat a Wilcoxon signed-rank teszt eredményét mutatja az egyes kombinációkon. Fontos megjegyezni, hogy a szignifikanciaértékeket az SPSS Statistics nem igazította ki a többszörös összehasonlítások kompenzálására – az SPSS Statistics által előállított szignifikanciaértékeket kézzel kell összehasonlítania az Ön által kiszámított Bonferroni-korrigált szignifikanciaértékkel. Láthatjuk, hogy a p < 0,017 szignifikancia szinten csak a zene nélküli és a tánc (tánc-nincs, p = 0,008) közötti észlelt erőfeszítés különbözött statisztikailag szignifikánsan.
SPSS statisztika
A Friedman-teszt eredményének jelentése (post hoc tesztekkel)
A Friedman-teszt post hoc tesztekkel eredményeit a következőképpen jelentheti:
- Általános
Az érzékelt erőfeszítésben statisztikailag szignifikáns különbség volt attól függően, hogy futás közben milyen típusú zenét hallgattak, χ2(2) = 7.600, p = 0.022. Post hoc elemzést végeztünk Wilcoxon előjeles rangsor tesztekkel, Bonferroni korrekció alkalmazásával, melynek eredményeként a szignifikancia szintet p < 0,017-ben határoztuk meg. A zene nélküli, a klasszikus és a tánczenei futópróbában az észlelt erőfeszítés mediánja (IQR) 7,5 (7-8), 7,5 (6,25-8), illetve 6,5 (6-7) volt. Nem volt szignifikáns különbség a zene nélküli és a klasszikus zenei futópróbák (Z = -0,061, p = 0,952), illetve a klasszikus és a tánczenei futópróbák (Z = -1,811, p = 0,070) között, annak ellenére, hogy az észlelt erőfeszítés összességében csökkent a tánczenei és a klasszikus futópróbák között. Ugyanakkor statisztikailag szignifikánsan csökkent az észlelt erőfeszítés a tánczene vs. zene nélküli kísérletben (Z = -2,636, p = 0,008).
Leave a Reply