Egy szelíd bevezetés a konvex héj problémájába

A konvex héjak sokféle területen hasznosak, néha egészen váratlanul. Ebben a cikkben elmagyarázom a 2d konvex héjak alapötletét, és azt, hogy hogyan használjuk a Graham-próbát a megtalálásukhoz. Tehát ha már ismered a graham-szkennelést, akkor ez a cikk nem neked szól, de ha nem, akkor ez megismertet téged néhány releváns fogalommal.

Egy ponthalmaz konvex burkát úgy definiáljuk, hogy az a legkisebb konvex sokszög, amely a halmaz összes pontját magába foglalja. A konvex azt jelenti, hogy a sokszögnek nincs befelé hajló sarka.

A jobb oldali sokszög piros élei azt a sarkot zárják körül, ahol az alakzat homorú, vagyis a konvex ellentéte.

A konvex héjról való gondolkodás hasznos módja a gumiszalag analógia. Tegyük fel, hogy a halmaz pontjai szögek, amelyek egy sík felületből állnak ki. Képzeljük el most, mi történne, ha fognánk egy gumiszalagot, és megfeszítenénk a szögek körül. A gumiszalag megpróbálna visszahúzódni az eredeti hosszára, és körbezárná a szögeket, érintve azokat, amelyek a középponttól a legtávolabb állnak ki.

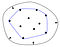
Az így kapott konvex burkot kódban ábrázolva általában azoknak a pontoknak a listáját tároljuk, amelyek ezt a gumiszalagot tartják, azaz a konvex burkon lévő pontok listáját.

Megjegyezzük, hogy még meg kell határoznunk, mi történjen, ha három pont ugyanazon a vonalon fekszik. Ha úgy képzeljük el, hogy a gumiszalagnak van egy olyan pontja, ahol az egyik szöget érinti, de ott egyáltalán nem hajlik, akkor ez azt jelenti, hogy az ott lévő szög két másik szög közötti egyenesre fekszik. A feladattól függően ezt a szöget az egyenes mentén a kimenet részének tekinthetjük, mivel megérinti a gumiszalagot. Másrészt azt is mondhatjuk, hogy ez a szög nem lehet a kimenet része, mert a gumiszalag alakja nem változik, ha eltávolítjuk. Ez a döntés attól függ, hogy éppen milyen problémán dolgozunk, és a legjobb, ha olyan bemenetünk van, ahol nincs három olyan pont, amelyik kollineáris (ez gyakran előfordul a programozási versenyek könnyű feladataiban), akkor akár teljesen figyelmen kívül is hagyhatjuk ezt a problémát.

A konvex héj megtalálása

A ponthalmazra nézve az emberi intuíció segítségével gyorsan kitalálhatjuk, hogy mely pontok érintik valószínűleg a konvex héjat, és melyek lesznek közelebb a középponthoz, és így távol a konvex héjtól. Ennek az intuíciónak a kódba való átültetése azonban némi munkát igényel.

Egy ponthalmaz konvex burkának megtalálására használhatjuk a Graham Scan nevű algoritmust, amelyet a számítógépes geometria egyik első algoritmusának tartanak. Ezzel az algoritmussal megtalálhatjuk a konvex héjon fekvő pontok részhalmazát, valamint azt a sorrendet, amelyben ezek a pontok a konvex héj körbejárása során találkoznak.

Az algoritmus egy olyan pont keresésével kezdődik, amelyről biztosan tudjuk, hogy a konvex héjon fekszik. A legalacsonyabb y koordinátával rendelkező pont például biztos választásnak tekinthető. Ha több pont is létezik ugyanazon az y koordinátán, akkor azt vesszük, amelyiknek a legnagyobb az x koordinátája (ez más sarokpontokkal is működik, pl. először a legalacsonyabb x, majd a legalacsonyabb y).

A továbbiakban a többi pontot aszerint rendezzük, hogy a kezdőpontból nézve milyen szögben helyezkednek el. Ha két pont történetesen azonos szögben van, akkor a kiindulási ponthoz közelebb eső pontnak kell előbbre kerülnie a rendezésben.

Az algoritmus lényege most az, hogy körbejárjuk ezt a rendezett tömböt, minden pont esetében meghatározva, hogy az a konvex héjon fekszik-e vagy sem. Ez azt jelenti, hogy minden egyes ponthármas esetében, amellyel találkozunk, eldöntjük, hogy azok konvex vagy konkáv sarkot alkotnak-e. Ha a sarok homorú, akkor tudjuk, hogy a hármasból a középső pont nem feküdhet a konvex héjon.

(Megjegyezzük, hogy a homorú és konvex sarok kifejezéseket a teljes sokszögre vonatkoztatva kell használni, csak egy sarok önmagában nem lehet konvex vagy homorú, hiszen akkor nem lenne referenciairány.)

A konvex héjon fekvő pontokat egy veremben tároljuk, így hozzáadhatunk pontokat, ha a rendezett pontokat körbejárva elérjük őket, és eltávolíthatjuk őket, ha kiderül, hogy konkáv sarkot alkotnak.

(Szigorúan véve a verem felső két pontjához kell hozzáférnünk, ezért helyette std::vector-t használunk, de gondoljunk rá úgy, mint egyfajta veremre, mert mindig csak a felső pár elemre vagyunk kíváncsiak.)

A rendezett ponttömb körül haladva hozzáadjuk a pontot a veremhez, és ha később kiderül, hogy a pont nem tartozik a konvex héjhoz, akkor eltávolítjuk.

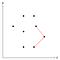
A keresztszorzat kiszámításával és annak ellenőrzésével, hogy az pozitív vagy negatív, meg tudjuk mérni, hogy az aktuális sarok befelé vagy kifelé hajlik. A fenti ábrán egy olyan ponthármas látható, ahol az általuk alkotott sarok konvex, ezért a három pont közül egyelőre a középső marad a veremben.

A következő pontra lépve ugyanezt folytatjuk: megnézzük, hogy a sarok konvex-e, és ha nem, akkor eltávolítjuk a pontot. Ezután folytassuk a következő pont hozzáadásával és ismételjük.

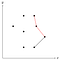
Ez a pirossal jelölt sarok konkáv, ezért a középső pontot eltávolítjuk a veremről, mivel nem lehet része a konvex burkolatnak.

Honnan tudjuk, hogy így megkapjuk a helyes választ?

A szigorú bizonyítás megírása nem tartozik ennek a cikknek a keretébe, de az alapötleteket le tudom írni. Arra bátorítalak azonban, hogy folytasd, és próbáld meg kitölteni a hiányosságokat!

Mivel minden sarkon kiszámítottuk a kereszttöredéket, biztosan tudjuk, hogy egy konvex sokszöget kapunk. Most már csak azt kell bebizonyítanunk, hogy ez a konvex sokszög valóban minden pontot magába foglal.

(Valójában azt is meg kell mutatnunk, hogy ez a lehető legkisebb konvex sokszög, amely kielégíti ezeket a feltételeket, de ez elég könnyen következik abból, hogy a konvex sokszögünk sarokpontjai az eredeti ponthalmaz részhalmazai.)

Tegyük fel, hogy létezik egy P pont az imént megtalált sokszögön kívül.

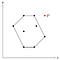
Mivel minden pont egyszer került a halmazba, tudjuk, hogy P valamikor lekerült a halmazról. Ez azt jelenti, hogy P a szomszédos pontjaival, nevezzük őket O-nak és Q-nak, együtt egy homorú sarkot alkotott.

Mivel O és Q a sokszögön belül (vagy annak határán) fekszik, P-nek is a határon belül kellene feküdnie, mert a sokszög konvex, és az a sarok, amit O és Q P-vel alkot, a sokszöghöz képest homorú.

Ezzel ellentmondást találtunk, ami azt jelenti, hogy ilyen P pont nem létezhet.

Implementáció

Az itt megadott implementációnak van egy convex_hull függvénye, amely egy std::vectort vesz, amely a pontokat std::pairs ints-ként tartalmazza, és egy másik std::vectort ad vissza, amely a konvex héjon fekvő pontokat tartalmazza.

Futási idő és memóriaelemzés

A bonyolultsági algoritmusokról mindig hasznos a Big-O jelölés szempontjából gondolkodni, amit itt nem magyarázok el, mert Michael Olorunnisola itt már sokkal jobban elmagyarázta, mint én valószínűleg tenném:

A pontok rendezése kezdetben O(n log n) időt vesz igénybe, de utána minden lépés állandó idő alatt kiszámítható. Minden pont legfeljebb egyszer kerül a veremre és legfeljebb egyszer kerül le a veremről, ez azt jelenti, hogy a legrosszabb esetben a futási idő O(n log n).

A memóriahasználat, ami jelenleg O(n)-ben van, optimalizálható lenne, ha megszüntetnénk a verem szükségességét és a műveleteket közvetlenül a bemeneti tömbön végeznénk. A konvex héjon fekvő pontokat a bemeneti tömb elejére mozgathatnánk és a megfelelő sorrendbe rendezhetnénk, a többi pont pedig a tömb többi részébe kerülne. A függvény ekkor csak egyetlen egészértékű változót adhatna vissza, amely a tömb azon pontjainak mennyiségét jelöli, amelyek a konvex héjon fekszenek. Ennek persze megvan az a hátulütője, hogy a függvény sokkal bonyolultabbá válik, ezért nem javasolnám, hacsak nem beágyazott rendszerekre kódolsz, vagy hasonlóan korlátozó memóriakérdésekkel rendelkezel. A legtöbb helyzetben a hibavalószínűség/memória megtakarítás kompromisszum egyszerűen nem éri meg.

Más algoritmusok

A Graham Scan alternatívája a Chan algoritmus, amely gyakorlatilag ugyanazon az ötleten alapul, de könnyebben megvalósítható. Érdemes azonban először megérteni, hogyan működik a Graham Scan.

Ha igazán fantáziadúsak vagyunk, és három dimenzióban akarjuk megoldani a problémát, vessünk egy pillantást Preparata és Hong algoritmusára, amelyet 1977-ben mutattak be “Convex Hulls of Finite Sets of Points in Two and Three Dimensions” című dolgozatukban.