Differenciálegyenletek – Sajátértékek és sajátfüggvények
Megjelenítjük a mobil értesítést Minden jegyzet megjelenítése Minden jegyzet elrejtése
8-2. szakasz : Sajátértékek és sajátfüggvények
Az előző szakaszhoz hasonlóan ismét meg kell jegyeznünk, hogy csak röviden fogunk foglalkozni a sajátértékek és sajátfüggvények témakörével a peremértékproblémák esetében. Elég sok olyan elképzelés van, amelyet itt nem fogunk megvizsgálni. Ennek a szakasznak csupán az a célja, hogy képet adjon a témáról, és elegendő munkát végezzen ahhoz, hogy a következő fejezetben megoldhassunk néhány alapvető parciális differenciálegyenletet.
Most, mielőtt elkezdenénk beszélni a szakasz tényleges témájáról, idézzünk fel egy témát a lineáris algebrából, amelyet korábban röviden tárgyaltunk ebben a jegyzetben. Egy adott négyzetes mátrixra, \(A\), ha \(\lambda \) olyan értékeket találunk, amelyekre nem nulla megoldást, azaz \(\vec x \ne \vec 0\), találunk,
\
akkor \(\lambda \) az \(A\) sajátértékének neveztük, és \(\vec x\) volt a megfelelő sajátvektor.
Fontos itt felidézni, hogy ahhoz, hogy \(\lambda \) sajátérték legyen, akkor az egyenletnek nem nullától eltérő megoldásokat kellett találnunk.
Szóval, mi köze van ennek a határértékproblémákhoz? Nos, térjünk vissza az előző részhez, és nézzük meg a 7. és 8. példát. Ebben a két példában homogén (és ez fontos!) BVP-ket oldottunk meg,
\
A 7. példában \(\lambda = 4\) volt, és nemtriviális (azaz nem nulla) megoldásokat találtunk a BVP-re. A 8. példában \(\lambda = 3\) volt, és az egyetlen megoldás a triviális megoldás volt (azaz \(y\left( t \right) = 0\)). Úgy tűnik tehát, hogy ez a homogén BVP (emlékezzünk vissza, ez azt is jelenti, hogy a peremfeltételek nulla) hasonló viselkedést mutat, mint a fenti mátrixegyenlet viselkedése. Vannak olyan \(\lambda \) értékek, amelyek nem triviális megoldásokat adnak erre a BVP-re, és olyan \(\lambda \) értékek, amelyek csak a triviális megoldást engedik meg.
Az \(\lambda \) azon értékeire, amelyek nem triviális megoldásokat adnak, az \(\lambda \) értéket a BVP sajátértékének nevezzük, a nem triviális megoldásokat pedig az adott sajátértéknek megfelelő BVP sajátfüggvényeinek.
Most már tudjuk, hogy az \(\eqref{eq:eq1}\) \(\lambda = 4\) egy sajátérték (\(y\left( x \right) = {c_2}\sin \left( {2x} \right)\) sajátfüggvényekkel) és hogy \(\lambda = 3\) nem sajátérték.
A végén megpróbáljuk meghatározni, hogy van-e más sajátérték az \(\eqref{eq:eq1}\) számára, azonban mielőtt ezt megtennénk, kommentáljuk röviden, hogy miért olyan fontos, hogy a BVP homogén legyen ebben a vitában. Az előző szakasz 2. és 3. példájában a homogén differenciálegyenletet
\
két különböző nemhomogén peremfeltétellel oldottuk meg,
\
A két példában láttuk, hogy \(a\) és/vagy \(b\) értékének egyszerű megváltoztatásával vagy nemtriviális megoldásokat kaptunk, vagy egyáltalán nem tudtunk megoldást kikényszeríteni. A sajátértékek/eigenfüggvények tárgyalása során szükségünk van arra, hogy létezzenek megoldások, és ezt a viselkedést csak úgy tudjuk biztosítani, ha megköveteljük, hogy a peremfeltételek is homogének legyenek. Más szóval, szükségünk van arra, hogy a BVP homogén legyen.
Van még egy utolsó téma, amit meg kell beszélnünk, mielőtt rátérnénk a sajátértékek és sajátfüggvények témájára, és ez inkább egy notációs kérdés, ami segíteni fog nekünk a későbbiekben elvégzendő munkánk egy részében.
Tegyük fel, hogy van egy másodrendű differenciálegyenletünk, és a karakterisztikus polinomnak két valós, különböző gyöke van, és ezek a következő alakúak
\
Akkor tudjuk, hogy a megoldás,
\
Míg ezzel a megoldással nincs semmi baj, írjuk át egy kicsit ezt. Kezdjük azzal, hogy felosztjuk a kifejezéseket a következőképpen,
\
Most összeadjuk/kivonjuk a következő kifejezéseket (figyeljük meg, hogy “összekeverjük” az \({c_i}\) és \( \pm \,\alpha \) az új kifejezésekben), hogy megkapjuk,
\
A következőben kicsit átrendezzük a kifejezéseket,
\
Végül a zárójelben lévő mennyiségek tényezőt és a tört helyét is áthelyezzük. Ha ezt megtesszük, valamint átnevezzük az új állandókat, akkor azt kapjuk,
\
Ez a sok munka valószínűleg nagyon titokzatosnak és feleslegesnek tűnik. Azonban valóban volt rá oka. Valójában talán már láttátok az okot, legalábbis részben. A két “új” függvény, amely a megoldásunkban szerepel, valójában két hiperbolikus függvény. Nevezetesen,
\
Az olyan másodrendű differenciálegyenlet megoldásának egy másik módja, amelynek karakterisztikus polinomja két valós, különböző gyökkel rendelkezik \({r_1} = \alpha ,\,\,\,{r_2} = – \,\alpha \) alakban,
\
Az, hogy néhány (valójában a legtöbb) általunk vizsgált probléma esetében a megoldás ilyen formában van, nagyban megkönnyíti az életünket. A hiperbolikus függvényeknek van néhány nagyon szép tulajdonságuk, amit ki tudunk (és ki is fogunk) használni.
Először is, mivel később szükségünk lesz rájuk, a deriváltak,
\
Ezután vessünk egy gyors pillantást e függvények grafikonjaira.
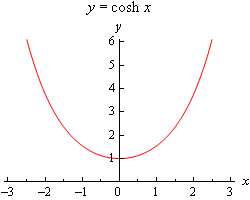

Megjegyezzük, hogy \(\cosh \left( 0 \right) = 1\) és \(\sinh \left( 0 \right) = 0\). Mivel gyakran fogunk \(x = 0\) peremfeltételekkel dolgozni, ezek hasznos értékek lesznek.
A következő, és talán még fontosabb, vegyük észre, hogy \(\cosh \left( x \right) > 0\) minden \(x\) esetén, és így a hiperbolikus koszinusz soha nem lesz nulla. Hasonlóképpen láthatjuk, hogy \(\sinh \left( x \right) = 0\) csak akkor, ha \(x = 0\). Mindkét tényt használni fogjuk néhány munkánk során, ezért nem szabad elfelejtenünk őket.
Oké, most, hogy mindezzel végeztünk, dolgozzunk egy példán, hogy lássuk, hogyan kell sajátértékeket/sajátfüggvényeket találni egy BVP-hez.
Ezzel a BVP-vel kezdtük ezt a szakaszt, és már ismerünk egy sajátértéket (\(\lambda = 4\)), és ismerjük \(\lambda \) egy olyan értékét, amely nem sajátérték (\(\lambda = 3\)). Az itt végzett munka során nem szabad elfelejtenünk, hogy akkor kapunk sajátértéket \(\lambda \) egy adott értékére, ha \(\lambda \) adott értékére nem triviális megoldásokat kapunk a BVP-re.
Azért, hogy tudjuk, hogy megtaláltuk az összes sajátértéket, nem kezdhetjük csak úgy véletlenszerűen próbálgatni \(\lambda \) értékeit, hogy lássuk, nem triviális megoldásokat kapunk-e vagy sem. Szerencsére van erre egy olyan módszer, ami nem túl rossz, és az összes sajátértéket/sajátfüggvényt megadja nekünk. Néhány esetet azonban meg kell csinálnunk. A három eset, amelyet meg kell vizsgálnunk, a következő : \(\lambda > 0\), \(\lambda = 0\) és \(\lambda < 0\). Mindegyik eset a BVP megoldásának egy sajátos formáját adja, amelyre aztán alkalmazhatjuk a peremfeltételeket, hogy lássuk, nem triviális megoldásokat kapunk-e vagy sem. Kezdjünk tehát hozzá az esetekhez.
\(\underline {\lambda > 0} \)
Ebben az esetben a differenciálegyenletből kapott karakterisztikus polinom a következő,
\
Ez esetben, mivel tudjuk, hogy \(\lambda > 0\) ezek a gyökök komplexek, így helyettük felírhatjuk őket,
\
A differenciálegyenlet általános megoldása tehát,
\
Az első peremfeltétel alkalmazásával megkapjuk,
\
Ezt figyelembe véve és a második peremfeltételt alkalmazva tehát,
\
Ez azt jelenti, hogy az alábbiak közül valamelyiknek meg kell lennie,
\
Megjegyezzük azonban, hogy nem triviális megoldásokat akarunk, és ha az első lehetőség van, akkor az \(\lambda > 0\) minden értékére a triviális megoldást kapjuk. Tegyük fel tehát, hogy \({c_2} \ne 0\). Ez azt jelenti, hogy van,
\
Más szóval, kihasználva azt a tényt, hogy tudjuk, hol a szinusz nulla, eljuthatunk a második egyenlethez. Vegyük észre azt is, hogy mivel feltételezzük, hogy \(\lambda > 0\), tudjuk, hogy \(2\pi \sqrt \lambda > 0\)és így \(n\) csak pozitív egész szám lehet ebben az esetben.
Most már csak meg kell oldanunk ezt \(\lambda \) esetén, és meglesz az összes pozitív sajátérték ehhez a BVP-hez.
A pozitív sajátértékek tehát,
\
és az ezeknek a sajátértékeknek megfelelő sajátfüggvények,
\
Megjegyeztük, hogy a sajátértékeken és sajátfüggvényeken egy \(n\)-t írtunk alá, hogy jelezzük, hogy az \(n\) minden adott értékére van egy. Vegyük észre azt is, hogy a \({c_2}\) jelet elhagytuk a sajátfüggvényeknél. A sajátfüggvények esetében csak maga a függvény érdekel minket, és nem az előtte lévő konstans, ezért ezt általában elhagyjuk.
Lépjünk most a második esetre.
\(\underline {\lambda = 0} \)
Ez esetben a BVP a következő lesz,
\
és a differenciálegyenlet néhányszoros integrálásával megkapjuk az általános megoldást,
\
Az első peremfeltétel alkalmazásával megkapjuk,
\
A második peremfeltétel, valamint az első peremfeltétel eredményeit alkalmazva,
\
Ez esetben, az első esettől eltérően, nem választhatjuk meg, hogy ezt nullára állítjuk. Ez csak akkor lesz nulla, ha \({c_2} = 0\).
Ezért erre a BVP-re (és ez fontos), ha \(\lambda = 0\) az egyetlen megoldás a triviális megoldás, és így \(\lambda = 0\) nem lehet sajátérték erre a BVP-re.
Most nézzük az utolsó esetet.
\(\underline {\lambda < 0} \)
Ez esetben a karakterisztikus egyenlet és annak gyökei ugyanazok, mint az első esetben. Tehát tudjuk, hogy,
\
Mivel azonban, mivel itt \(\lambda < 0\) feltételezzük, ezek most két valós, különböző gyök, és így a fenti, ilyen valós, különböző gyökökre vonatkozó munkánkat felhasználva tudjuk, hogy az általános megoldás az lesz,
\
Megjegyezzük, hogy itt használhattuk volna a megoldás exponenciális formáját is, de a munkánkat jelentősen megkönnyíti, ha itt a megoldás hiperbolikus formáját használjuk.
Most az első peremfeltétel alkalmazásával megkapjuk,
\
A második peremfeltétel alkalmazásával megkapjuk,
\
Mivel \(\lambda < 0\) feltételezzük, tudjuk, hogy \(2\pi \sqrt { – \lambda } \ne 0\) és így azt is tudjuk, hogy \(\sinh \left( {2\pi \sqrt { – \lambda } } \right) \ne 0\). Ezért a második esethez hasonlóan \({c_2} = 0\) kell lennie.
Ezért erre a BVP-re (ez megint fontos), ha \(\lambda < 0\), akkor csak a triviális megoldást kapjuk, és így nincsenek negatív sajátértékek.
Összefoglalva tehát a következő sajátértékeket/sajátfüggvényeket kapjuk erre a BVP-re.
\
Nézzünk egy másik példát kissé eltérő peremfeltételekkel.
Itt derivált peremfeltételekkel fogunk dolgozni. A munka azonban nagyjából megegyezik az előző példával, ezért itt nem fogunk olyan részletesen foglalkozni vele. Az előző példához hasonlóan mindhárom eseten végig kell mennünk, úgyhogy kezdjünk hozzá.
\(\underline {\lambda > 0} \)
A differenciálegyenlet általános megoldása megegyezik az előző példával, tehát van,
\
Az első peremfeltétel alkalmazásával megkapjuk,
\
Megjegyezzük, hogy itt azt feltételezzük, hogy \(\lambda > 0\), így ez csak akkor lesz nulla, ha \({c_2} = 0\). Most a második peremfeltétel azt adja,
\
Emlékezzünk vissza, hogy nem akarunk triviális megoldásokat, és hogy \(\lambda > 0\) tehát csak akkor kapunk nem-triviális megoldást, ha azt követeljük meg,
\
Megoldva \(\lambda \) és látjuk, hogy pontosan ugyanazokat a pozitív sajátértékeket kapjuk erre a BVP-re, mint az előző példában.
\
Az ezeknek a sajátértékeknek megfelelő sajátfüggvények azonban,
\
Szóval erre a BVP-re a pozitív sajátértékeknek megfelelő sajátfüggvényekhez koszinuszokat kapunk.
Most a második eset.
\(\underline {\lambda = 0} \)
Az általános megoldás,
\
Az első peremfeltételt alkalmazva,
\
Az általános megoldás ezután,
\
és megjegyezzük, hogy ez triviálisan kielégíti a második peremfeltételt,
\
Ezért az első példával ellentétben \(\lambda = 0\) egy sajátérték ehhez a BVP-hez, és az ennek a sajátértéknek megfelelő sajátfüggvények a következők,
\
Még egyszer megjegyezzük, hogy a sajátfüggvényeknél elhagytuk a tetszőleges konstansot.
Végül foglalkozzunk a harmadik esettel.
\(\underline {\lambda < 0} \)
Az általános megoldás itt az,
\
Az első peremfeltétel alkalmazása adja,
\
A második peremfeltétel alkalmazása adja,
\
Az előző példához hasonlóan ismét tudjuk, hogy \(2\pi \sqrt { – \lambda } \ne 0\) és így \(\sinh \left( {2\pi \sqrt { – \lambda } } \right) \ne 0\). Ezért \({c_1} = 0\).
Ezért erre a BVP-re ismét nincs negatív sajátértékünk.
Összefoglalva tehát a következő sajátértékeket/sajátfüggvényeket kapjuk erre a BVP-re.
\
Megjegyezzük azt is, hogy ezeket valójában kombinálhatjuk, ha megengedjük, hogy az első \(n\) listája egy helyett nullával kezdődjön. Ez gyakran nem fog előfordulni, de amikor igen, akkor kihasználjuk. Tehát a sajátértékek/eigenfüggvények “hivatalos” listája ehhez a BVP-hez a következő,
\
Az előző két példában láttuk, hogy általában különböző eseteket kell figyelembe vennünk az \(\lambda \) esetében, mivel a különböző értékek gyakran különböző általános megoldásokhoz vezetnek. Ne ragaszkodjunk túlságosan azokhoz az esetekhez, amelyeket itt tettünk. Többnyire ezt a bizonyos differenciálegyenletet fogjuk megoldani, ezért csábító lesz azt feltételezni, hogy mindig ezeket az eseteket fogjuk vizsgálni, de vannak olyan BVP-k, amelyek más/különböző eseteket igényelnek.
Amint a két példában láttuk, néha egy vagy több eset nem ad sajátértéket. Ez gyakran előfordul, de megint csak nem szabad semmit kiolvasnunk abból, hogy a két BVP egyikénél sem kaptunk negatív sajátértéket. Vannak olyan BVP-k, amelyeknek negatív sajátértékei lesznek.
Nézzünk egy másik példát egy nagyon eltérő peremfeltételekkel. Ezek nem a hagyományos peremfeltételek, amelyeket eddig vizsgáltunk, de a következő fejezetben látni fogjuk, hogyan merülhetnek fel ezek bizonyos fizikai problémákból.
Ebben a példában tehát valójában nem fogjuk megadni a megoldást vagy annak deriváltját a határoknál. Ehelyett egyszerűen megadjuk, hogy a megoldásnak a két határon azonosnak kell lennie, és a megoldás deriváltjának is azonosnak kell lennie a két határon. Emellett az ilyen típusú peremfeltétel jellemzően egy intervallum alakú lesz, ahelyett, ahogyan eddig dolgoztunk.
Amint már említettük, az ilyen típusú peremfeltételek nagyon természetesen fordulnak elő bizonyos fizikai problémákban, és ezt a következő fejezetben meg is fogjuk látni.
Az előző két példához hasonlóan még mindig a szokásos három esetet kell megvizsgálnunk.
\(\underline {\lambda > 0} \)
Az általános megoldás erre az esetre a következő,
\
Az első peremfeltételt alkalmazva és felhasználva azt a tényt, hogy a koszinusz páros függvény (azaz.\(\cos \left( { – x} \right) = \cos \left( x \right)\)) és hogy a szinusz egy páratlan függvény (azaz \(\sin \left( { – x} \right) = – \sin \left( x \right)\)). ad,
\
Az előző két példával ellentétben ezúttal ez nem mond semmit. Lehet, hogy \(\sin \left( {\pi \sqrt \lambda } \right) = 0\), de az is teljesen lehetséges, a probléma ezen pontján egyébként, hogy \({c_2} = 0\) is.
Szóval, menjünk tovább, és alkalmazzuk a második peremfeltételt, és nézzük meg, hogy kapunk-e belőle valamit.
\
Szóval, valami nagyon hasonlót kapunk, mint amit az első peremfeltétel alkalmazása után kaptunk. Mivel feltételezzük, hogy \(\lambda > 0\), ez azt jelenti, hogy vagy \(\sin \left( {\pi \sqrt \lambda } \right) = 0\) vagy \({c_1} = 0\).
Megjegyezzük azonban, hogy ha \(\sin \left( {\pi \sqrt \lambda } \right) \ne 0\), akkor \({c_1} = {c_2} = 0\) és akkor a triviális megoldást kapjuk. Ezért meg kell követelnünk, hogy \(\sin \left( {\pi \sqrt \lambda } \right) = 0\) és így, ahogy az előző két példánál is tettük, most megkapjuk a sajátértékeket,
\
Visszatérve arra, hogy \(\lambda > 0\) és láthatjuk, hogy a lehetséges \(n\) értékek listáját nulla helyett eggyel kell kezdeni.
Az eset sajátértékeit tehát már ismerjük, de mi a helyzet a sajátfüggvényekkel. A megoldás egy adott sajátértékre az,
\
és nincs okunk feltételezni, hogy a két állandó közül bármelyik nulla vagy nem nulla, ami azt illeti. Ilyen esetekben két sajátfüggvénykészletet kapunk, egy-egy konstansnak megfelelőt. A sajátfüggvények két csoportja ebben az esetben a következő,
\
Most a második eset.
\(\underline {\lambda = 0} \)
Az általános megoldás,
\
Az első peremfeltételt alkalmazva,
\
Az általános megoldás ezután,
\
és megjegyezzük, hogy ez triviálisan kielégíti a második peremfeltételt, ahogy a fenti második példában láttuk. Ezért ismét \(\lambda = 0\) a BVP sajátértéke, és az ennek a sajátértéknek megfelelő sajátfüggvények a következők,
\
Végül foglalkozzunk a harmadik esettel.
\(\underline {\lambda < 0} \)
Az általános megoldás itt is,
\
Az első peremfeltételt alkalmazva és felhasználva azt a tényt, hogy a hiperbolikus koszinusz páros, a hiperbolikus szinusz pedig páratlan, megkapjuk,
\
Most, ebben az esetben feltételezzük, hogy \(\lambda < 0\) és így tudjuk, hogy \(\pi \sqrt { – \lambda } \ne 0\), ami viszont azt mondja, hogy \(\sinh \left( {\pi \sqrt { – \lambda } } \right) \ne 0\). Ezért \({c_2} = 0\) kell, hogy legyen.
Most alkalmazzuk a második peremfeltételt, hogy megkapjuk,
\
Az \(\lambda \) feltételezésünk alapján itt sem tehetünk mást, mint hogy \({c_1} = 0\).
Ezért ebben az esetben az egyetlen megoldás a triviális megoldás, és így erre a BVP-re ismét nincs negatív sajátértékünk.
Összefoglalva tehát a következő sajátértékeket/sajátfüggvényeket kapjuk erre a BVP-re.
\
Megjegyezzük, hogy elismertük, hogy az \(\lambda > 0\) esetében két sajátfüggvénykészletünk volt azzal, hogy külön-külön felsoroltuk őket. Emellett az utóbbi kettőt ismét egyesíthetjük a sajátértékek és sajátfüggvények egy halmazává. Így a következő sajátérték- és sajátfüggvényhalmazt kapjuk.
\
Még egyszer kaptunk egy olyan példát, amelynek nincsenek negatív sajátértékei. Nem győzzük elégszer hangsúlyozni, hogy ez inkább a differenciálegyenlet függvénye, amivel dolgozunk, és lesznek olyan példák, amelyekben negatív sajátértékeket kaphatunk.
Most, eddig a pontig csak egy differenciálegyenlettel dolgoztunk, ezért dolgozzunk egy példát egy másik differenciálegyenlettel, csak hogy megbizonyosodjunk arról, hogy nem ragaszkodunk túlságosan ehhez az egy differenciálegyenlethez.
Mielőtt ezzel a példával dolgoznánk, jegyezzük meg, hogy a példáink túlnyomó többségét továbbra is azzal az egy differenciálegyenlettel fogjuk dolgozni, amit eddig használtunk. Csak azért dolgozunk ezzel a másik differenciálegyenlettel, hogy ne ragaszkodjunk túlságosan egyetlen differenciálegyenlet használatához.
Ez egy Euler-differenciálegyenlet, és így tudjuk, hogy meg kell találnunk a következő kvadratikus gyökeit.
\
Ez a kvadratikus gyökei a következők,
\
Most, itt ismét lesz néhány eset, amivel dolgozhatunk, azonban ezek nem ugyanazok lesznek, mint az előző példák. A megoldás attól függ, hogy a gyökerek valós különállóak, kettősek vagy komplexek, és ezek az esetek az \(1 – \lambda \) előjelétől/értékétől függnek. Vegyük tehát végig az eseteket.
\(\underline {1 – \lambda < 0,\,\,\,\lambda > 1} \)
Ebben az esetben a gyökök komplexek lesznek, és a megoldás felírásához a következőképpen kell felírnunk őket.
\
A gyökök ilyen módon való felírásával tudjuk, hogy \(\lambda – 1 > 0\) és így \(\sqrt {\lambda – 1} \) már valós szám, amire szükségünk van ahhoz, hogy felírjuk a következő megoldást,
\
Az első peremfeltételt alkalmazva megkapjuk,
\
A második peremfeltétel alkalmazásával megkapjuk,
\
Azért, hogy elkerüljük a triviális megoldást ebben az esetben,
\
Ez sokkal bonyolultabb feltétel, mint amit eddig láttunk, de ettől eltekintve ugyanazt tesszük. Tehát az \(\lambda \) megoldása a következő sajátérték-halmazt adja erre az esetre.
\
Megjegyezzük, hogy az \(n\) listáját nem nullával, hanem eggyel kell kezdenünk, hogy biztosan \(\lambda > 1\) legyen, ahogyan azt erre az esetre feltételezzük.
Az ezeknek a sajátértékeknek megfelelő sajátfüggvények a következők,
\
Most a második eset.
\(\underline {1 – \lambda = 0,\,\,\,\,\,\lambda = 1} \)
Ebben az esetben az \ kettős gyökét kapjuk({r_{\\,1,2}} = – 1\) és így a megoldás,
\
Az első peremfeltétel alkalmazása adja,
\
A második peremfeltétel alapján,
\
Ez esetben tehát csak a triviális megoldást kapjuk, így \(\lambda = 1\) nem sajátérték.
Foglalkozzunk most a harmadik (és egyben utolsó) esettel.
\(\underline {1 – \lambda > 0,\,\,\,\lambda < 1} \)
Ez az eset két különböző valós gyökkel rendelkezik, és a megoldás,
\
Az első peremfeltétel alkalmazásával megkapjuk,
\
Ezt felhasználva a megoldásunk a következő lesz,
\
A második peremfeltételt alkalmazva,
\
Most, mivel tudjuk, hogy \(\lambda \ne 1\) ebben az esetben a zárójelben lévő két tagon az exponensek nem azonosak, így a zárójelben lévő tag nem nulla. Ez azt jelenti, hogy csak az lehet,
\
és így ebben az esetben csak a triviális megoldásunk van, és nincs olyan sajátérték, amelyre \(\lambda < 1\).
Az egyetlen sajátértékek ehhez a BVP-hez ekkor az első esetből származnak.
Az eddig használt “standard” differenciálegyenlettől eltérő differenciálegyenletet használó példát dolgoztunk fel. Ahogy azonban a munkában láttuk, az alapfolyamat nagyjából ugyanaz volt. Megállapítottuk, hogy számos olyan eset van (itt három, de nem mindig három lesz), amelyek különböző megoldásokat adnak. Minden egyes esetet megvizsgáltunk, hogy megállapítsuk, lehetségesek-e nem triviális megoldások, és ha igen, akkor megtaláltuk az adott esetnek megfelelő sajátértékeket és sajátfüggvényeket.
Még egy utolsó példát kell kidolgoznunk ebben a részben, mielőtt elhagyjuk ezt a részt néhány új témával. A négy példa, amivel eddig dolgoztunk, mind meglehetősen egyszerű volt (az egyszerű persze relatív…), azonban nem akarunk elmenni anélkül, hogy elismerjük, hogy sok sajátérték/sajátérték-probléma ennyire egyszerű.
Sok példában még az sem lehetséges, hogy egy BVP összes lehetséges sajátértékének teljes listáját megkapjuk. Gyakran az egyenleteket, amelyeket meg kell oldanunk, hogy megkapjuk a sajátértékeket, nehéz, ha nem lehetetlen pontosan megoldani. Nézzünk meg tehát egy ilyen példát, hogy lássuk, milyen dolgokat lehet tenni, hogy legalább képet kapjunk arról, hogyan néznek ki a sajátértékek ilyen esetekben.
A peremfeltételek ehhez a BVP-hez meglehetősen különböznek azoktól, amelyekkel eddig dolgoztunk. Az alapvető folyamat azonban ugyanaz. Kezdjük tehát az első esettel.
\(\underline {\lambda > 0} \)
A differenciálegyenlet általános megoldása megegyezik az első néhány példával, és így van,
\
Az első peremfeltétel alkalmazásával megkapjuk,
\
A második peremfeltételt,
\
Ha tehát \({c_2} = 0\), akkor a triviális megoldást kapjuk, és így ahhoz, hogy ezt a peremfeltételt teljesítsük, ehelyett azt kell megkövetelnünk, hogy,
\
Most, ennek az egyenletnek vannak megoldásai, de néhány numerikus technikát kell alkalmaznunk ahhoz, hogy megkapjuk őket. Hogy lássuk, mi történik itt, ábrázoljuk \(\tan \left( {\sqrt \lambda } \right)\) és \( – \sqrt \lambda \) ugyanazon a grafikonon. Itt van ez a grafikon, és figyeljük meg, hogy a vízszintes tengely valójában az \(\sqrt \lambda \) értékei, mivel ez megkönnyíti a dolgok áttekintését és a számunkra ismerős értékekhez való viszonyítását.

A sajátértékek tehát ebben az esetben ott fognak előfordulni, ahol a két görbe metszi egymást. Az első ötöt megmutattuk a grafikonon, és ismétlem, ami a grafikonon látszik, az valójában a tényleges sajátérték négyzetgyöke, ahogy azt már megjegyeztük.
Az érdekes dolog itt az, hogy minél távolabb vagyunk a grafikonon, annál közelebb kerülnek a sajátértékek az érintő aszimptotáihoz, és így ezt kihasználva azt mondjuk, hogy elég nagy \(n\) esetén a sajátértékeket az érintő aszimptotáinak (nagyon jól ismert) helyeivel tudjuk közelíteni.
Az, hogy mekkora az \(n\) értéke, mielőtt elkezdjük használni a közelítést, attól függ, hogy mekkora pontosságot akarunk, de mivel ismerjük az aszimptoták helyét, és ahogy \(n\) nő, úgy nő a közelítés pontossága is, így elég könnyű lesz ellenőrizni egy adott pontosságot.
A példa szempontjából az első ötöt numerikusan találtuk meg, majd a többi sajátérték közelítését fogjuk használni. Íme ezek az értékek/közelítések.
\
Az első öt után zárójelben lévő szám az aszimptóta közelítő értéke. Amint láthatjuk, ezek egy kicsit eltérnek, de mire eljutunk \(n = 5\), a közelítés hibája 0,9862%. Tehát kevesebb, mint 1% a hiba, mire elérjük az \(n = 5\) értéket, és csak jobb lesz, ha az \(n\) értéke nagyobb lesz.
A sajátfüggvények erre az esetre a következők,
\
ahol az \({\lambda _{\,n}}\) értékeit fentebb adtuk meg.
Szóval, most, hogy mindezzel a munkával végeztünk, nézzük meg a második esetet.
\(\underline {\lambda = 0} \)
Az általános megoldás,
\
Az első peremfeltételt alkalmazva,
\
Az általános megoldás ezután,
\
A második peremfeltételt erre alkalmazva,
\
Ezért ebben az esetben csak a triviális megoldást kapjuk, és így \(\lambda = 0\) nem sajátérték. Megjegyezzük azonban, hogy ha a második peremfeltétel \(y’\left( 1 \right) – y\left( 1 \right) = 0\) lett volna, akkor \(\lambda = 0\) egy sajátérték lenne (\(y\left( x \right) = x\) sajátfüggvényekkel), és így ismét óvatosnak kell lennünk, nehogy túl sokat olvassunk bele a munkánkba.
Végül foglalkozzunk a harmadik esettel.
\(\underline {\lambda < 0} \)
Az általános megoldás itt az,
\
Az első peremfeltétel alkalmazása adja,
\
Az általános megoldás így lesz,
\
A második peremfeltételt alkalmazva erre,
\
Most, feltételezésből tudjuk, hogy \(\lambda < 0\) és így \(\sqrt { – \lambda } > 0\). Ez viszont azt mondja, hogy \(\sinh \left( {\sqrt { – \lambda } } \right) > 0\) és tudjuk, hogy \(\cosh \left( x \right) > 0\) minden \(x\) esetén. Ezért
\
és így \({c_2} = 0\) és ismét ebben a harmadik esetben a triviális megoldást kapjuk, és így ennek a BVP-nek nem lesznek negatív sajátértékei.
Összefoglalva, az egyetlen sajátértékek ehhez a BVP-hez abból származnak, hogy feltételezzük, hogy \(\lambda > 0\), és ezeket a fentiekben adtuk meg.
Ebben a részben tehát több sajátérték/eigenfüggvény példát dolgoztunk fel. Mielőtt elhagynánk ezt a részt, még egyszer meg kell jegyeznünk, hogy rengeteg különböző problémával dolgozhatunk itt, és tényleg csak egy puszta maréknyi példát mutattunk, ezért kérem, ne menjenek el ebből a részből abban a hitben, hogy mindent megmutattunk.
Az egész rész célja az, hogy felkészítsen minket azokra a problématípusokra, amelyekkel a következő fejezetben találkozunk majd. Emellett a következő fejezetben ismét néhány meglehetősen alapvető és egyszerű problémára fogunk szorítkozni, hogy a parciális differenciálegyenletek megoldásának egyik elterjedtebb módszerét szemléltessük.
Leave a Reply