Bilineáris szűrés és bilineáris interpoláció

Nézze meg az alábbi képet. Ki tudod számolni az A,B és C pontokban lévő értékeket?

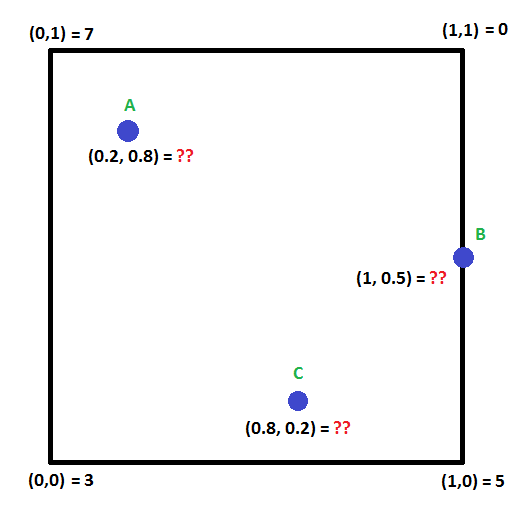
Létezik erre egy technika, az úgynevezett bilineáris interpoláció, amely a lineáris interpoláció ötletét két dimenzióra terjeszti ki.

A bilineáris interpoláció kiszámításához egyszerűen lineáris interpolációt végzel az egyik tengelyen, majd a másikon.

Nézd meg ezeket a példákat:

A pont
A pont koordinátája (0.2,0.8). Kezdjük az X tengellyel.

Először interpolációt végzünk a négyzet tetején az X tengelyen. Ez azt jelenti, hogy 0,2 (20%) utat kell megtennünk 7-től 0-ig. Ez a 0,2 az X tengely koordinátánk. Ennek kiszámításához így járunk el:
7 + (0-7) * 0,2 = 5,6

Ezután interpolációt végzünk a négyzet alján az X tengelyen. Tehát a fentiekhez hasonlóan 0,2 (20%) utat teszünk meg 3-tól 5-ig. Ennek kiszámításához ezt tesszük:
3 + (5-3) * 0,2 = 3,4

Most, hogy interpoláltunk az X tengelyen, interpolálnunk kell az Y tengelyen. Most az alsó értékünktől (az Y = 0 értékétől) a felső értékünkig (az Y = 1 értékéig) 0,8 (80%) fogunk eljutni. Az alsó érték az általunk elvégzett alsó interpoláció (3,4), a felső érték pedig az általunk elvégzett felső interpoláció (5,6).

Szóval, a 3,4-től az 5,6-ig tartó út 0,8 (80%) részét kell megtennünk. Ennek kiszámításához a következőt tesszük:
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Az A pontban lévő érték tehát 5,16. Az alábbi kép segíthet vizuálisan elmagyarázni a folyamatot, amin keresztülmentünk.

B pont

A B pont koordinátái (1.0,0.5).

Kezdjük újra az X tengelyű interpolációval (bár könnyen kezdhetjük először az Y tengellyel, ha akarjuk! Ugyanahhoz az eredményhez jutnál).

Az X tengely interpolációját felülről végezve, 1,0 (100%) utat kell megtennünk 7-től 0-ig. Biztos vagyok benne, hogy kitalálod, mi a válasz, de itt van kiszámolva:
7 + (0-7) * 1,0 = 0

Hasonlóképpen, végezzük el az X tengely interpolációját alulról. A 3-tól 5-ig tartó út 1,0 (100%) részét kell megtennünk.
3 + (5-3) * 1,0 = 5

A következő lépés az Y tengely interpolációja. Az út 0,5 (50%) részét kell megtennünk 5-től 0-ig.
5 + (0-5) * 0,5 = 2,5

Íme, a B pont értéke 2,5. Ennek is érthetőnek kell lennie, ha megnézzük a diagramot. Ez alapvetően 1d lineáris interpoláció 5 és 0 között, és a kettő között félúton van, így intuitíve a 2,5 válasznak értelmesnek kell lennie.

C pont

A C pont koordinátája (0,8,0,2).

Még egyszer végezzük el az X tengely interpolációt a doboz tetején. A 7-ről 0,8 (80%) távolságra kell mennünk 0.
7 + (0-7) * 0,8 = 1,4

Ezután végezzük el az X tengelyes interpolációt a doboz alján. A 3-tól 5-ig tartó út 0,8 (80%) részét kell megtennünk.
3 + (5-3) * 0,8 = 4,6

Végre az y tengely interpolációja. A 4,6-tól 0,2 (20%) távolságra kell mennünk 1,4-ig.
4,6 + (1,4-4,6) * 0,2 = 3,96

A C pont értéke 3.96

Bilineáris szűrés

Míg a bilineáris interpoláció hasznos, ha van egy adatháló, amelyen belül interpolálni szeretnénk az értékeket (például egy magasságmező, amely a terepet reprezentálja?!), ahol ez igazán ragyog a játékfejlesztésben, az a bilineáris textúraszűrés.

Lényegében, ha van egy textúrakoordinátád, amely nem esik tökéletesen egybe a textúra egy pixelének középpontjával (mert van egy maradék), akkor a koordináta törtrészét használja a pixelen belül, hogy bilineáris interpolációt végezzen a 4 érintett pixel között, hogy megkapja a végső pixel színét. Bilineáris interpolációt végez minden egyes csatornán:

A végeredmény elég jó! Nézd meg az alábbi képen, hogy láthasd működés közben egy textúrán, amit túlságosan nagyítottunk. A bal oldal bilineáris szűrést használ, míg a jobb oldal nem, és csak a legközelebbi pixelt mutatja.

A bilineáris textúraszűrésnek következésképpen 4 pixeles olvasást kell végeznie, hogy interpolálni tudjon közöttük, ahelyett, hogy egyetlen pixeles olvasást végezne, mint amikor a legközelebbi pixeles mintavételt alkalmazzuk. Több pixelolvasás = több overhead, és nem olyan olcsó (számítási szempontból) a használata.

Linkek

Azoknak, akik ezt olvassák, ez az információ elég alapvető, és talán csodálkoznak, hogy miért fáradoztam azzal, hogy írjak róla. Nézzétek meg a következő hozzászólásban valami elég bizarr dolgot a bilineáris szűréssel kapcsolatban. Erre szükség volt, mint ugródeszkára a következő dologhoz, amit meg akarok mutatni nektek 😛

Wikipedia: Bilineáris interpoláció

Wikipedia: Lineáris interpoláció

Wikipedia: Bilineáris interpoláció

Wikipedia:

The Dark Side of Bilinear Filtering

Nézd meg ezeket a linkeket a hardveres bilineáris mintavételezés néhány hiányosságáról (és néhány megoldásról):
iq: hardware interpolation
iq: improved texture interpolation