Bevezetés a dekonvolúcióba

A dekonvolúció egy számításigényes képfeldolgozási technika, amelyet egyre gyakrabban alkalmaznak a mikroszkópban rögzített digitális képek kontrasztjának és felbontásának javítására. Az alapok egy sor olyan módszerre épülnek, amelyek célja a mikroszkópos képeken jelenlévő, az objektív korlátozott apertúrája által kiváltott elmosódás eltávolítása vagy visszafordítása.

Majdnem minden digitális fluoreszcens mikroszkóppal felvett kép dekonvolválható, és számos új alkalmazás van fejlesztés alatt, amelyek dekonvolúciós technikákat alkalmaznak a különböző kontrasztnövelő stratégiákkal felvett átmenő fényű képekre. A dekonvolúcióval történő javításra leginkább alkalmas témák közé tartoznak az optikai metszetek sorozatából felépített háromdimenziós montázsok.

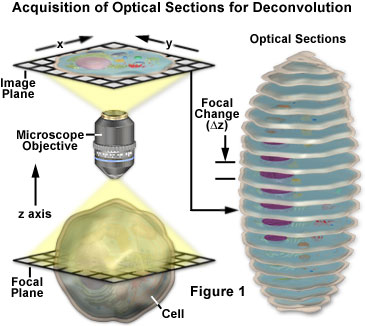
A z-sorozatú képek dekonvolúciós elemzésre történő felvételét övező alapfogalmakat az 1. ábra vázlatos ábrával mutatja be. A mintáról a z tengely mentén egymástól kissé eltolt képsorozatot rögzítünk. Ez a fókuszsík-változás egy kissé eltérő képet eredményez, amelynek finom változásait az aktuális z-sík fölülről és alulról érkező, fókuszon kívüli fény okozza. A dekonvolúciós elemzés során a teljes z-sorozatot elemzik, hogy egy tisztább, nagyobb felbontású adatsort hozzanak létre, amelyet nem zavar a fókuszon kívüli fluoreszcencia.

A dekonvolúciót gyakran javasolják a konfokális mikroszkóp jó alternatívájaként, mivel mindkét technika arra törekszik, hogy minimalizálja a fókuszon kívüli fluoreszcencia hatását a végső képre… Ez nem teljesen igaz, mert a konfokális mikroszkópban pinhole-apertúrával készült képek esetében a dekonvolúciós feldolgozás előnyös. A konfokális mikroszkópia megakadályozza a fókuszon kívüli fény észlelését azáltal, hogy az objektív és a detektor közé egy lyuknyílást helyez, amelyen csak a fókuszban lévő fénysugarak juthatnak át. Ezzel szemben a szélesmezős mikroszkópok lehetővé teszik, hogy a fókuszon kívüli fény közvetlenül a detektorra jusson. Az így kapott képekre dekonvolúciót alkalmaznak, hogy vagy kivonják a fókuszon kívüli fényt, vagy visszavezessék azt a forrásához. A konfokális mikroszkópia különösen alkalmas vastag minták, például embriók vagy tüskék vizsgálatára, míg a szélesmezős dekonvolúciós feldolgozás hatékony eszköznek bizonyult a rendkívül alacsony megvilágítást igénylő minták képalkotásához. Ezeket az eszközöket akár kombinálni is lehet a konfokális mikroszkóppal készült képek zajának csökkentésére. Az irodalomban közölt dekonvolúciós kísérletek többsége azonban standard szélesmezős fluoreszcenciamikroszkóppal rögzített képekre vonatkozik.

A képromlás forrásai

A képromlás négy független forrásra osztható: zaj, szórás, tükröződés és elmosódás. A 2. ábra példákat mutat be ezek vizuális hatására ugyanazon a képen.

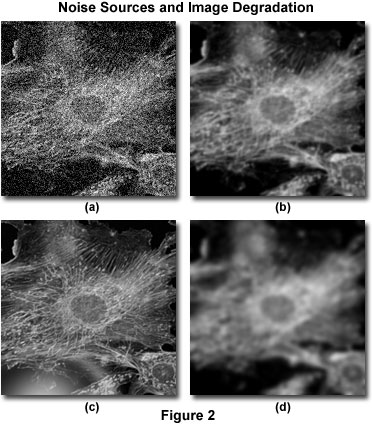
A zaj úgy írható le, mint a kép részleteinek kvázi véletlenszerű rendezetlensége, amely (legsúlyosabb formájában) a fehér zaj vagy a sós-borsos zaj látszatát kelti, hasonlóan ahhoz, amit a televíziós adásokban rossz vétel esetén látunk (2.a ábra). Ezt a fajta zajt “kvázi-véletlenszerűnek” nevezik, mivel a statisztikai eloszlás megjósolható, ha a forrás mechanikája ismert. A digitális mikroszkópiában a zaj fő forrása vagy maga a jel (gyakran fotonlövési zajnak nevezik), vagy a digitális képalkotó rendszer. Mindkét zajforrás mechanikája ismert, ezért a zaj statisztikai eloszlása ismert. A jelfüggő zaj Poisson-eloszlással jellemezhető, míg a képalkotó rendszerből származó zaj gyakran Gauss-eloszlást követ. Mivel a digitális képeken előforduló általános zaj forrása és eloszlása jól ismert, könnyen eltávolítható a megfelelő képszűrők alkalmazásával, amelyeket a legtöbb dekonvolúciós szoftvercsomag általában opcionális “előfeldolgozási” rutinként tartalmaz.

A szórást általában a fény véletlenszerű zavarának nevezik, amelyet a törésmutató változása okoz a mintában. A szórás nettó hatása a kép részleteinek valóban véletlenszerű rendezetlensége, ahogyan az a 2(b) ábrán látható. Bár egyelőre nem dolgoztak ki teljesen kielégítő módszert egy adott minta szórásának előrejelzésére, bebizonyosodott, hogy a szórás mértéke nagymértékben függ a minta vastagságától, valamint a minta és a környező beágyazó anyagok optikai tulajdonságaitól. A szórás növekszik mind a minta vastagságával, mind a mintán belüli belső komponensek törésmutatójának heterogenitásával.

A szóráshoz hasonlóan a káprázás is a fény véletlenszerű zavarása, de nem a mintán belül, hanem a mikroszkóp optikai elemeiben (lencsék, szűrők, prizmák stb.) jelentkezik. A modern mikroszkópokban a tükröződéscsökkentő bevonattal ellátott lencsék és szűrők alkalmazásával, valamint a lencseképzési technikák, az optikai cementek és az üvegkészítmények tökéletesítésével sikerült minimalizálni a tükröződés mértékét. A 2. (c) ábra a kontrollálatlan tükröződés hatását szemlélteti.

A homályosságot a fény nem véletlenszerű eloszlásával írják le, amely a képalkotó rendszer optikai útvonalán való áthaladás során keletkezik (2. (d) ábra). Az elmosódás legjelentősebb forrása a diffrakció, és azt a képet, amelynek felbontását csak az elmosódás korlátozza, diffrakciósan korlátozottnak tekintjük. Ez minden képalkotó rendszer belső korlátját jelenti, és ez a meghatározó tényező az optikai rendszer felbontási határának megítélésében. Szerencsére az optikai mikroszkópban lévő elmosódás kifinomult modelljei állnak rendelkezésre, amelyek felhasználhatók a fókuszon kívüli fotonok forrásának meghatározására. Ez az alapja a dekonvolúciónak. A dekonvolúcióban betöltött alapvető jelentősége miatt az elmosódás elméleti modelljét e szakasz más részeiben sokkal részletesebben tárgyaljuk. Hangsúlyozni kell azonban, hogy minden képalkotó rendszer elmosódást produkál, függetlenül a képminta vagy a kísérő műszerelektronika által kiváltott képromlás egyéb formáitól. Pontosan az optikai elmosódásnak az egyéb romlástípusoktól való függetlensége teszi lehetővé az elmosódás dekonvolúciós technikákkal történő eltávolítását.

A fénynek az anyaggal való kölcsönhatása a szórás, a tükröződés és az elmosódás elsődleges fizikai eredete. Egy adott anyag (legyen az üveg, víz vagy fehérje) molekuláinak összetétele és elrendeződése azonban minden anyagot sajátos optikai tulajdonságokkal ruház fel. A dekonvolúció szempontjából a szórást, a tükröződést és az elmosódást az különbözteti meg, hogy hol fordulnak elő, és hogy lehetőség van e jelenségek matematikai modelljének létrehozására. Mivel a szórás lokalizált, szabálytalan jelenség, amely a mintadarabon fordul elő, nehezen modellezhetőnek bizonyult. Ezzel szemben, mivel a homályosság a mikroszkóp optikai rendszerének (elsősorban az objektívnek) a függvénye, viszonylag egyszerűen modellezhető. Egy ilyen modell lehetővé teszi az elmosódási folyamat matematikai visszafordítását, és a dekonvolúció ezt a modellt használja az elmosódás visszafordítására vagy eltávolítására.

A pontterjedési függvény

Az elméleti optikában kialakult elmosódás modellje a háromdimenziós pontterjedési függvény (PSF) fogalmán alapul. Ez a fogalom alapvető fontosságú a dekonvolúció szempontjából, és a képalkotási műtermékek elkerülése érdekében világosan meg kell érteni. A pontterjedési függvény alapja egy végtelenül kicsi, a minta (tárgy) teréből származó pontszerű fényforrás. Mivel a mikroszkóp képalkotó rendszere az e pont által kibocsátott fénynek csak egy töredékét gyűjti be, nem tudja a fényt a pont tökéletes háromdimenziós képére fókuszálni. Ehelyett a pont háromdimenziós diffrakciós mintázattá szélesedve és szétterülve jelenik meg. Így a pontterjedési függvényt formálisan úgy definiáljuk, mint egy ideális pontszerű fényforrás által létrehozott háromdimenziós diffrakciós mintázatot.

Az alkalmazott képalkotási módtól függően (szélesmezős, konfokális, átmenő fény) a pontterjedési függvénynek más és más alakja és kontúrja van. Szélesmezős fluoreszcenciamikroszkópban a pontterjedési függvény alakja egy hosszúkás “labda” fényhez hasonlít, amelyet szélesedő gyűrűkből álló fáklya vesz körül. A pontterjedési függvény három dimenzióban történő leírásához általában egy három tengelyes (x, y és z) koordinátarendszert alkalmaznak, ahol az × és y párhuzamos a minta fókuszsíkjával, a z pedig párhuzamos a mikroszkóp optikai tengelyével. Ebben az esetben a pontterjedési függvény az x-y síkban koncentrikus gyűrűk halmazaként jelenik meg, az x-z és y-z síkokban pedig homokórára hasonlít (amint azt a 3. ábra szemlélteti). A szélesmezős pontterjedési függvény középpontján áthaladó x-y szelet koncentrikus gyűrűk halmazát mutatja: az úgynevezett Airy-korongot, amelyre a klasszikus optikai mikroszkópiáról szóló szövegekben gyakran hivatkoznak.

A 3. ábrán a gömbi aberráció különböző fokozatait mutató pontterjedési függvények két x-z vetülete látható. Az optikai tengely párhuzamos a kép függőleges tengelyével. A bal oldali pontterjedési függvény minimális szférikus aberrációt mutat, míg a jobb oldali jelentős mértékű aberrációt. Vegyük észre, hogy a jobb oldali képen a tengelyirányú aszimmetria és a központi csomópont kiszélesedése az optikai tengely mentén a tengelyirányú felbontás romlásához és a jel elmosódásához vezet. Elméletileg a pontterjedési függvény mérete végtelen, és a fókusztól távoli síkokban a fény összesített összegzett intenzitása megegyezik a fókuszban lévő összegzett intenzitással. A fényintenzitás azonban gyorsan csökken, és végül megkülönböztethetetlenné válik a zajtól. Egy nagy numerikus rekesznyílású (1,40) olajmerülő objektívvel felvett, rendezetlen pontterjedési függvényben a fókusz síkjában 0,2 négyzetmikrométert elfoglaló fény a fókusz fölött és alatt 1 mikrométerrel 90-szer nagyobb területre terjed szét. A pontterjedési függvény képeinek rögzítéséhez használt minta egy 0,1 mikrométer átmérőjű fluoreszcens gyöngy volt, amelyet glicerinbe (törésmutatója 1,47) szereltek, az ábrán feltüntetett törésmutatójú merülőolajokkal.

Fontos szempont, hogy a pontterjedési függvény hogyan befolyásolja a mikroszkópban a képalkotást. A képalkotás elméleti modellje a pontterjedési függvényt a kép alapegységeként kezeli. Más szóval a pontterjedési függvény olyan a képhez, mint a tégla a házhoz. A legjobb kép, ami valaha is lehet, a pontterjedési függvények összessége, és a nagyítás növelése nem változtat ezen a tényen. Ahogy egy ismert elméleti optika tankönyv (Born és Wolf: Principles of Optics) kifejti: “Az okulár erősségének növelésével lehetetlen olyan részleteket kiemelni, amelyek nincsenek jelen az elsődleges képen, mivel az elsődleges kép minden egyes eleme egy kis diffrakciós minta, és az okulár által látott tényleges kép csak e minták nagyított képeinek együttese.”

Példaként tekintsünk egy fedőlemez és egy mikroszkóplemez közé szorított, alulfelbontású fluoreszcens gyöngyökből álló populációt. Ennek a mintának a fókuszba helyezett képe egy pontfelhőt mutat, amely valójában egy apró gyűrűkkel körülvett korong (valójában egy Airy-korong; lásd a 4. ábra (a)). Ha ezt a mintát kissé eltávolítjuk a fókuszból, koncentrikus gyűrűk nagyobb csoportja jelenik meg ott, ahol a fókuszált képen az egyes pontok voltak (4. ábra (b)). Ha erről a mintáról háromdimenziós képet gyűjtünk, akkor minden egyes gyöngyhöz egy teljes pontterjedési függvényt rögzítünk. A pontterjedési függvény leírja, hogy mi történik az egyes pontszerű fényforrásokkal, miután áthaladnak a képalkotó rendszeren.

Az imént leírt elmosódási folyamatot matematikailag konvolúcióként modellezik. A konvolúciós művelet a pontterjedési függvénynek a minta minden egyes pontjára történő alkalmazását írja le: a tárgy minden egyes pontjából kibocsátott fényt a végső kép előállításához a pontterjedési függvénnyel konvolváljuk. Sajnos ez a konvolúció azt eredményezi, hogy a mintadarab pontjai elmosódott régiókká válnak a képen. A kép minden egyes pontjának fényereje a konvolúciós művelet által lineárisan kapcsolódik a minta minden egyes pontjának fluoreszcenciájához. Mivel a pontterjedési függvény háromdimenziós, a pontterjedési függvényből származó elmosódás eredendően háromdimenziós jelenség. A bármely fókuszsíkból származó kép az adott síkban elhelyezkedő pontokból származó elmosódott fényt tartalmazza, amely keveredik a más fókuszsíkokból származó pontokból származó elmosódott fénnyel.

A helyzetet úgy lehet összefoglalni, hogy a képet a minta és a pontterjedési függvény konvolúciója alkotja. A dekonvolúció megfordítja ezt a folyamatot, és megpróbálja rekonstruálni a mintát egy elmosódott képből.

A pontterjedési függvény eltérései

A pontterjedési függvényt vagy elméletileg lehet meghatározni a diffrakció matematikai modelljének felhasználásával, vagy empirikusan egy fluoreszcens gyöngy háromdimenziós képének felvételével (lásd a 3. ábrát). Az elméleti pontterjedési függvény általában axiális és radiális szimmetriával rendelkezik. Valójában a pontterjedési függvény szimmetrikus az x-y sík felett és alatt (axiális szimmetria) és a z tengely körül (radiális szimmetria). Egy empirikus pontterjedési függvény jelentősen eltérhet a tökéletes szimmetriától (amint az a 3. ábrán látható). Ezt az eltérést, amelyet általában aberrációnak neveznek, a képalkotó rendszer optikai rendszerének bármely komponensében – különösen az objektívben – előforduló szabálytalanságok vagy helytelen beállítások okozzák, de más komponensek, például tükrök, sugárelosztók, tubuslencsék, szűrők, rekeszek és apertúrák esetében is előfordulhat. Minél jobb minőségűek az optikai alkatrészek és minél jobb a mikroszkóp igazítása, annál közelebb kerül az empirikus pontterjedési függvény az ideális szimmetrikus alakhoz. Mind a konfokális, mind a dekonvolúciós mikroszkópia attól függ, hogy a pontterjedési függvény minél közelebb legyen az ideális esethez.

Az optikai mikroszkópia során leggyakrabban előforduló aberráció, amelyet minden tapasztalt és profi mikroszkópos jól ismer, a szférikus aberráció. Ennek az aberrációnak a megnyilvánulása a pontterjedési függvény alakjának tengelyirányú aszimmetriája, ennek megfelelő méretnövekedéssel, különösen a z tengely mentén (3. ábra). Az eredmény a felbontás és a jelintenzitás jelentős csökkenése. A gyakorlatban a szférikus aberráció tipikus forrása az objektív frontlencse merítőközegének és a próbadarabot befogadó közeg törésmutatója közötti eltérés. Óriási hangsúlyt kell fektetni ennek az aberrációnak a minimalizálásának fontosságára. Bár a dekonvolúció részben helyreállíthatja az elveszett felbontást, semmilyen képfeldolgozás nem képes helyreállítani az elveszett jelet.