A rövid bevezetés a differenciális adatvédelembe
Aaruran Elamurugaiyan
A magánszféra számszerűsíthető. Még jobb, ha rangsorolhatjuk az adatvédelmet megőrző stratégiákat, és megmondhatjuk, melyik a hatékonyabb. Még jobb, ha olyan stratégiákat tervezhetünk, amelyek még a segédinformációkkal rendelkező hackerekkel szemben is robusztusak. És mintha ez nem lenne elég jó, mindezt egyszerre is megtehetjük. Ezek a megoldások, és még sok más, a differenciális adatvédelemnek nevezett valószínűségi elméletben rejlenek.
Itt a kontextus. Egy érzékeny adatbázist gondozunk (vagy kezelünk), és szeretnénk néhány statisztikát kiadni ezekből az adatokból a nyilvánosság számára. Biztosítanunk kell azonban, hogy egy ellenfél számára lehetetlen legyen visszafejteni az érzékeny adatokat abból, amit kiadtunk . Az ellenfél ebben az esetben egy olyan fél, akinek az a szándéka, hogy felfedje vagy megismerje legalább néhány érzékeny adatunkat. A differenciált adatvédelem megoldhatja azokat a problémákat, amelyek akkor merülnek fel, ha ez a három összetevő – érzékeny adatok, a statisztikákat közzétenni kívánó kurátorok és az érzékeny adatokat visszaszerezni kívánó ellenfelek – jelen vannak (lásd az 1. ábrát). Ez a visszafejtés az adatvédelem megsértésének egy fajtája.

De mennyire nehéz az adatvédelem megsértése? Nem lenne elég az adatok anonimizálása? Ha más adatforrásokból származó kiegészítő információkkal rendelkezik, az anonimizálás nem elég. Például 2007-ben a Netflix egy verseny keretében közzétette a felhasználói értékeléseinek egy adatkészletét, hogy kiderüljön, ki tudja-e felülmúlni a kollaboratív szűrő algoritmusát. Az adatkészlet nem tartalmazott személyazonosító információkat, de a kutatók még mindig képesek voltak a magánélet megsértésére; az adatkészletből eltávolított összes személyes információ 99%-át visszanyerték. Ebben az esetben a kutatók az IMDB-ből származó segédinformációkat használva törték fel a magánéletet.
Hogyan védekezhet bárki egy olyan ellenféllel szemben, aki ismeretlen és esetleg korlátlan segítséget kap a külvilágból? A differenciális adatvédelem megoldást kínál. A differenciálisan privát algoritmusok ellenállóak a segédinformációkat használó adaptív támadásokkal szemben. Ezek az algoritmusok arra támaszkodnak, hogy véletlenszerű zajt építenek be a keverékbe, így minden, amit a támadó kap, zajossá és pontatlanná válik, és így sokkal nehezebbé válik a magánélet megsértése (ha egyáltalán megvalósítható).
Zajos számlálás
Nézzünk egy egyszerű példát a zaj bejuttatására. Tegyük fel, hogy egy hitelminősítéseket tartalmazó adatbázist kezelünk (összefoglalva az 1. táblázat).
Ezzel a példával kapcsolatban tegyük fel, hogy a támadó azon személyek számát szeretné megtudni, akiknek rossz a hitelminősítése (ami 3). Az adatok érzékenyek, ezért nem fedhetjük fel az alapigazságot. Ehelyett egy olyan algoritmust fogunk használni, amely visszaadja az alapigazságot, N = 3, valamint némi véletlenszerű zajt. Ez az alapötlet (véletlenszerű zaj hozzáadása az alapigazsághoz) a differenciális adatvédelem kulcsa. Tegyük fel, hogy választunk egy L véletlen számot egy nulla központú Laplace-eloszlásból, amelynek szórása 2. Visszaadjuk az N+L-t. A szórás kiválasztását néhány bekezdés múlva megmagyarázzuk. (Ha még nem hallottál a Laplace-eloszlásról, lásd a 2. ábrát). Ezt az algoritmust “zajos számlálásnak” fogjuk nevezni.
Ha értelmetlen, zajos választ fogunk jelenteni, akkor mi értelme van ennek az algoritmusnak? A válasz az, hogy lehetővé teszi számunkra, hogy egyensúlyt teremtsünk a hasznosság és az adatvédelem között. Azt akarjuk, hogy a nagyközönség némi hasznosságot nyerjen az adatbázisunkból, anélkül, hogy érzékeny adatokat tárnánk egy esetleges ellenfél elé.
Mit kapna valójában az ellenfél? A válaszokat a 2. táblázatban közöljük.

Az ellenfél által kapott első válasz közel áll az alapigazsághoz, de nem egyenlő azzal. Ebben az értelemben az ellenfelet becsapják, a hasznosság biztosított, és a magánélet védelme biztosított. Többszöri próbálkozás után azonban képes lesz megbecsülni az alapigazságot. Ez az “ismételt lekérdezésekből történő becslés” a differenciális adatvédelem egyik alapvető korlátja . Ha a támadó elegendő lekérdezést tud végrehajtani egy differenciálisan titkos adatbázisban, akkor is meg tudja becsülni az érzékeny adatokat. Más szóval, egyre több lekérdezéssel az adatvédelem sérül. A 2. táblázat empirikusan szemlélteti ezt az adatvédelmi sérülést. Amint azonban látható, az 5 lekérdezésből származó 90%-os konfidenciaintervallum meglehetősen széles; a becslés még nem túl pontos.
Mennyire lehet pontos ez a becslés? Nézze meg a 3. ábrát, ahol többször lefuttattunk egy szimulációt, és ábrázoltuk az eredményeket .

Minden függőleges vonal a 95%-os megbízhatósági intervallum szélességét szemlélteti, a pontok pedig az ellenfél mintavételezett adatainak átlagát jelzik. Vegyük észre, hogy ezek az ábrák logaritmikus vízszintes tengellyel rendelkeznek, és hogy a zaj független és azonos eloszlású Laplace-véletlenváltozókból származik. Összességében az átlag kevesebb lekérdezéssel zajosabb (mivel a mintanagyságok kicsik). A várakozásoknak megfelelően a konfidenciaintervallumok szűkülnek, ahogy az ellenfél több lekérdezést végez (mivel a minta mérete nő, és a zaj átlagosan nulla lesz). Csak a grafikon szemrevételezéséből láthatjuk, hogy körülbelül 50 lekérdezés szükséges ahhoz, hogy tisztességes becslést adjunk.
Gondolkodjunk el ezen a példán. Mindenekelőtt azzal, hogy véletlenszerű zajt adtunk hozzá, megnehezítettük egy ellenfél számára az adatvédelem megsértését. Másodszor, az általunk alkalmazott rejtőzködési stratégia egyszerűen megvalósítható és érthető volt. Sajnos egyre több és több lekérdezéssel az ellenfél képes volt megközelíteni a valódi számot.
Ha növeljük a hozzáadott zaj varianciáját, jobban meg tudjuk védeni az adatainkat, de nem adhatunk egyszerűen bármilyen Laplace-zajt egy olyan függvényhez, amelyet el akarunk rejteni. Ennek az az oka, hogy a zaj mennyisége, amelyet hozzá kell adnunk, a függvény érzékenységétől függ, és minden függvénynek megvan a maga érzékenysége. Különösen a számláló függvény érzékenysége 1. Nézzük meg, mit jelent az érzékenység ebben az összefüggésben.
Ez érzékenység és a Laplace-mechanizmus
Egy függvény esetében:
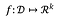
az f érzékenysége:
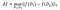
a legfeljebb egy elemben eltérő D₁, D₂ adathalmazokra .
A fenti definíció meglehetősen matematikai, de nem olyan rossz, mint amilyennek látszik. Durván szólva, egy függvény érzékenysége az a lehető legnagyobb különbség, amelyet egy sor az adott függvény eredményében okozhat, bármely adathalmaz esetében. Például a játékadathalmazunkban a sorok számolásának érzékenysége 1, mivel egyetlen sor hozzáadása vagy eltávolítása bármelyik adathalmazból legfeljebb 1-gyel változtatja meg a számolást.
Egy másik példaként tegyük fel, hogy a “számolás 5 többszörösére kerekítve” kifejezésre gondolunk. Ennek a függvénynek az érzékenysége 5, és ezt elég könnyen meg tudjuk mutatni. Ha van két 10 és 11 méretű adathalmazunk, ezek egy sorban különböznek egymástól, de az “5 többszörösére kerekített számok” 10, illetve 15. Valójában öt a lehető legnagyobb különbség, amit ez a példafüggvény produkálni tud. Ezért az érzékenysége 5.
Az érzékenység kiszámítása egy tetszőleges függvény esetében nehéz. Jelentős mennyiségű kutatási erőfeszítést fordítanak az érzékenységek becslésére , az érzékenység becslésének javítására és az érzékenység kiszámításának megkerülésére.
Hogyan kapcsolódik az érzékenység a zajos számláláshoz? A zajos számlálási stratégiánk egy Laplace-mechanizmusnak nevezett algoritmust használt, amely viszont az általa elhomályosított függvény érzékenységére támaszkodik . Az 1. algoritmusban a Laplace-mechanizmus naiv pszeudokódos megvalósítása található .
1. algoritmus
Bemenet: F függvény, X bemenet, adatvédelmi szint ϵ
Kimenet: F (X)
F F érzékenységének kiszámítása : S
L zajos válasz
Következtetés L zajról egy Laplace eloszlásból varianciával:
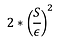
Hozd vissza F(X) + L
Minél nagyobb az S érzékenység, annál zajosabb lesz a válasz. A számlálásnak csak 1 érzékenysége van, így nem kell sok zajt hozzáadnunk az adatvédelem megőrzéséhez.
Megjegyezzük, hogy az 1. algoritmusban szereplő Laplace-mechanizmus epsilon paramétert fogyaszt. Ezt a mennyiséget a továbbiakban a mechanizmus adatvédelmi veszteségeként fogjuk emlegetni, és része a differenciális adatvédelmi terület legközpontibb definíciójának: az epsilon-differenciális adatvédelmi definíciónak. Szemléltetésképpen, ha felidézzük korábbi példánkat, és némi algebrát használunk, láthatjuk, hogy zajos számláló mechanizmusunk epsilon-differenciális adatvédelemmel rendelkezik, az epsilon értéke 0,707. Az epsilon beállításával szabályozhatjuk a zajos számlálás zajosságát. Ha kisebb epsilont választunk, akkor zajosabb eredményeket és jobb adatvédelmi garanciákat kapunk. Referenciaként az Apple 2 epsilont használ a billentyűzetük differenciálisan privát automatikus korrekciójában .
Az epsilon mennyisége az, ahogyan a differenciális adatvédelem szigorú összehasonlítást biztosíthat a különböző stratégiák között. Az epsilon-differenciális adatvédelem formális definíciója matematikailag egy kicsit bonyolultabb, ezért szándékosan kihagytam ebből a blogbejegyzésből. Bővebben olvashat róla Dwork áttekintésében a differenciális adatvédelemről .
Amint emlékszik, a zajos számlálási példa epsilonja 0,707 volt, ami elég kicsi. De még így is megsértettük az adatvédelmet 50 lekérdezés után. Miért? Mert a lekérdezések növekedésével nő az adatvédelmi költségvetés, és ezért rosszabb az adatvédelmi garancia.
Az adatvédelmi költségvetés
Az adatvédelmi veszteségek általában halmozódnak. Ha két választ kap vissza az ellenfél, a teljes adatvédelmi veszteség kétszer akkora, és az adatvédelmi garancia fele olyan erős. Ez a halmozódó tulajdonság az összetétel-tétel következménye. Lényegében minden egyes új lekérdezéssel további információk kerülnek nyilvánosságra az érzékeny adatokról. Ezért a kompozíciós tétel pesszimista szemléletű, és a legrosszabb esetet feltételezi: minden egyes új válasszal ugyanannyi szivárgás történik. Az erős adatvédelmi garanciákhoz azt szeretnénk, ha az adatvédelmi veszteség kicsi lenne. Tehát a mi példánkban, ahol harmincötös adatvédelmi veszteségünk van(50 lekérdezés után a Laplace zajos-számláló mechanizmusunkhoz), a megfelelő adatvédelmi garancia törékeny.
Hogyan működik a differenciális adatvédelem, ha az adatvédelmi veszteség ilyen gyorsan növekszik? Az értelmes adatvédelmi garancia biztosítása érdekében az adatkezelők érvényesíthetnek egy maximális adatvédelmi veszteséget. Ha a lekérdezések száma meghaladja a küszöbértéket, akkor az adatvédelmi garancia túl gyenge lesz, és a kurátor leállítja a lekérdezések megválaszolását. A maximális adatvédelmi veszteséget adatvédelmi költségvetésnek nevezzük. Minden egyes lekérdezésre úgy tekinthetünk, mint egy adatvédelmi “kiadásra”, amely fokozatos adatvédelmi veszteséget okoz. A költségvetések, kiadások és veszteségek használatának stratégiáját találóan adatvédelmi elszámolásnak nevezzük .
Az adatvédelmi elszámolás hatékony stratégia az adatvédelmi veszteség kiszámítására több lekérdezés után, de még mindig tartalmazhatja a kompozíciós tételt. Mint korábban említettük, az összetétel-tétel a legrosszabb esetet feltételezi. Más szóval léteznek jobb alternatívák.
Mély tanulás
A mély tanulás a gépi tanulás egy részterülete, amely a mély neurális hálózatok (DNN-ek) képzésére vonatkozik ismeretlen függvények becslésére. (Magas szinten egy DNN affin és nemlineáris transzformációk sorozata, amely egy n-dimenziós teret egy m-dimenziós térre képez le). Alkalmazásai széles körben elterjedtek, és itt nem szükséges megismételni őket. Magánosan fogjuk megvizsgálni, hogyan lehet egy mély neurális hálózatot képezni.
A mély neurális hálózatokat jellemzően a sztochasztikus gradiens ereszkedés (SGD) egy változatával képzik. Abadi és társai feltalálták ennek a népszerű algoritmusnak egy adatvédelmet megőrző változatát, amelyet általában “privát SGD”-nek (vagy PSGD-nek) neveznek. A 4. ábra szemlélteti az új technikájukban rejlő erőt . Abadi et al. feltalált egy új megközelítést: a momentumszámlálót. A pillanatok könyvelőjének alapgondolata a magánélet-kiadások felhalmozása azáltal, hogy a magánélet-veszteséget véletlen változóként keretezi, és a pillanatok generáló függvényeit használja a változó eloszlásának jobb megértéséhez (innen a név) . A teljes technikai részletek kívül esnek egy bevezető blogbejegyzés keretein, de javasoljuk, hogy olvassa el az eredeti tanulmányt, ha többet szeretne megtudni.

Végső gondolatok
Áttekintettük a differenciális adatvédelem elméletét, és láttuk, hogyan használható az adatvédelem számszerűsítésére. Az ebben a bejegyzésben szereplő példák megmutatják, hogyan alkalmazhatók az alapgondolatok, valamint az alkalmazás és az elmélet közötti kapcsolatot. Fontos megjegyezni, hogy az adatvédelmi garanciák többszöri használattal romlanak, ezért érdemes elgondolkodni azon, hogyan lehet ezt mérsékelni, akár adatvédelmi költségvetéssel, akár más stratégiákkal. A romlást erre a mondatra kattintva és kísérleteink megismétlésével vizsgálhatja meg. Még mindig sok itt megválaszolatlan kérdés van, és rengeteg szakirodalom vár felfedezésre – lásd az alábbi hivatkozásokat. További olvasásra biztatjuk Önt.
Cynthia Dwork. Differenciális magánélet: Az eredmények áttekintése. International Conference on Theory and Applications of Models of Computation, 2008.
Wikipedia Contributors. Laplace-eloszlás, 2018. július.
Aaruran Elamurugaiyan. Plots demonstrating standard error of differentially private responses over number of queries. 2018. augusztus.
Benjamin I. P. Rubinstein és Francesco Alda. Fájdalommentes véletlenszerű differenciális magánélet érzékenységi mintavétellel. In 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork and Aaron Roth. A differenciális adatvédelem algoritmikus alapjai . Now Publ., 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar és Li Zhang. Mélytanulás differenciális adatvédelemmel. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security – CCS16 , 2016.
Frank D. McSherry. Adatvédelemmel integrált lekérdezések: Egy bővíthető platform az adatvédelmet megőrző adatelemzéshez. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, pages 19-30, New York, NY, USA, 2009. ACM.
Wikipedia Hozzájárulók: ACM.
Wikipédia. Mélytanulás, 2018. augusztus.
Leave a Reply