9.5 – Befolyásoló adatpontok azonosítása

Ebben a szakaszban a következő két mértéket ismerjük meg a befolyásoló adatpontok azonosítására:

• Difference in Fits (DFFITS)
• Cook’s Distances

Az alapötlet mindkét mérték mögött ugyanaz, nevezetesen a megfigyelések egyesével történő törlése, minden alkalommal újraillesztve a regressziós modellt a fennmaradó n-1 megfigyelésre. Ezután összehasonlítjuk az összes n megfigyelést használó eredményeket az i-edik megfigyelés törlésével kapott eredményekkel, hogy lássuk, mekkora befolyása van a megfigyelésnek az elemzésre. Így elemezve képesek vagyunk felmérni, hogy az egyes adatpontok milyen potenciális hatással vannak a regresszióelemzésre.

Az illesztések különbsége (DFFITS)

Az i megfigyelésre vonatkozó illesztések különbsége, amelyet DFFITSi jelöli, a következőképpen van meghatározva:

\

Amint látható, a számláló az i-edik adatpontnak az elemzésből való bevonása és kizárása esetén kapott előrejelzett válaszok különbségét méri. A nevező az előre jelzett válaszok különbségének becsült szórása. Az illesztési különbség tehát azt számszerűsíti, hogy az illesztett érték hány standard eltéréssel változik, amikor az i-edik adatpontot kihagyjuk.

Egy megfigyelés akkor tekinthető befolyásosnak, ha DFFITS-értékének abszolút értéke nagyobb, mint:

\

melyben, mint mindig, n = a megfigyelések száma és k = a prediktortételek száma (azaz a regressziós paraméterek száma az intercept kivételével). Fontos szem előtt tartani, hogy ez nem egy szigorú szabály, hanem csak egy iránymutatás! Nem nehéz megtalálni a különböző szerzőket, akik kissé eltérő irányelvet használnak. Ezért én gyakran egy sokkal szubjektívebb iránymutatást részesítek előnyben, például azt, hogy egy adatpont akkor tekinthető befolyásosnak, ha a DFFITS-értékének abszolút értéke kiemelkedik a többi DFFITS-érték közül. Természetesen ez egy minőségi megítélés, talán úgy is kell lennie, mivel a kiugró értékek természetüknél fogva szubjektív mennyiségek.

Példa #2 (ismét). Nézzük meg az illeszkedések különbségének mértékét erre az adathalmazra (influence2.txt):

Regresszáljuk y-t x-re, és az illeszkedések különbségét kérve a következő szoftverkimenetet kapjuk:

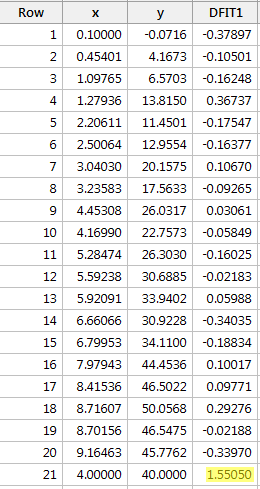
A fentebb meghatározott objektív irányelv alapján egy adatpontot akkor tekintünk befolyásosnak, ha DFFITS-értékének abszolút értéke nagyobb, mint:

\

Egyetlen adatpont – a piros – rendelkezik olyan DFFITS-értékkel, amelynek abszolút értéke (1.55050) nagyobb, mint 0,82. Ezért ezen irányelv alapján a piros adatpontot befolyásolónak tekintjük.

3. példa (ismét). Nézzük meg az illeszkedés mértékének különbségét erre az adathalmazra (influence3.txt):

Regresszáljuk y-t x-re, és az illesztések különbségét kérve a következő szoftverkimenetet kapjuk:

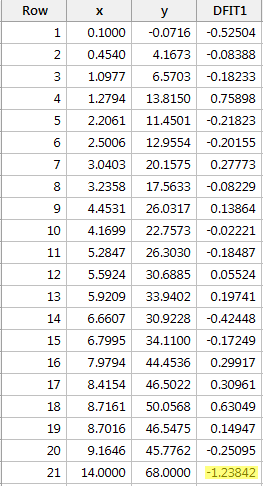
A fentebb meghatározott objektív irányelv alapján egy adatpontot akkor tekintünk befolyásosnak, ha DFFITS-értékének abszolút értéke nagyobb, mint:

\

Egyetlen adatpont – a piros – rendelkezik olyan DFFITS-értékkel, amelynek abszolút értéke (1.23841) nagyobb, mint 0,82. Ezért ezen irányelv alapján a piros adatpontot befolyásolónak tekintjük.

Az óra elején, amikor ezt az adathalmazt tanulmányoztuk, úgy döntöttünk, hogy a piros adatpont nem befolyásolja túlságosan a regresszióelemzést. Itt azonban az illeszkedés mértékének különbsége azt sugallja, hogy valóban befolyásos. Mi folyik itt? Minden annak felismerésén múlik, hogy a leckében szereplő összes intézkedés csak olyan eszköz, amely az adatelemző számára jelzi a potenciálisan befolyásoló adatpontokat. Végül az elemzőnek kétszer kell elemeznie az adathalmazt – egyszer a megjelölt adatpontokkal, egyszer pedig azok nélkül. Ha az adatpontok jelentősen megváltoztatják a regresszióelemzés eredményét, akkor a kutatónak mindkét elemzés eredményeit jelentenie kell.

Ezzel a példával kapcsolatban itt, ha azt a szubjektívebb iránymutatást használjuk, hogy a DFFITS-érték abszolút értéke kilóg-e, mint egy fájó hüvelykujj, akkor valószínűleg nem fogjuk a piros adatpontot befolyásolónak tekinteni. Végül is a következő legnagyobb DFFITS-érték (abszolút értékben) 0,75898. Ez a DFFITS-érték nem sokban különbözik a “befolyásos” adatpontunk DFFITS-értékétől.

4. példa (ismét). Nézzük meg az illeszkedések különbségének mértékét erre az adathalmazra (influence4.txt):

Regresszáljuk y-t x-re, és az illesztések különbségét kérve a következő szoftverkimenetet kapjuk:

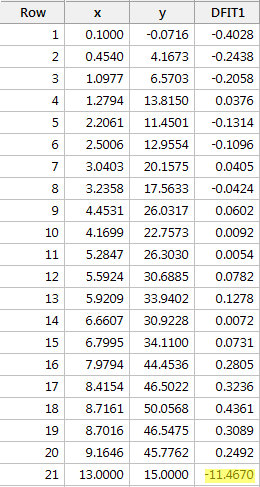
A fentebb meghatározott objektív irányelvet alkalmazva ismét befolyásolónak tekintünk egy adatpontot, ha a DFFITS értékének abszolút értéke nagyobb, mint:

\

Mi a véleménye? Van olyan DFFITS-érték, amelyik kilóg a sorból? Errr – a piros adatpont DFFITS-értéke (-11,4670 ) biztosan más nagyságrendű, mint az összes többi. Ebben az esetben aligha lehet kétséges, hogy a piros adatpont befolyásoló tényező!

Cook távolsága

A Cook-féle távolság mértékét, amelyet Di-vel jelölünk, a következőképpen határozzuk meg:

\.\]

Ez egy kicsit kuszának tűnik, de a legfontosabb dolog, amit fel kell ismerni, hogy a Cook-féle Di függ mind a maradéktól, ei (az első kifejezésben), mind a tőkeáttételtől, hii (a második kifejezésben). Vagyis az adatpont x értéke és y értéke is szerepet játszik a Cook-féle távolság kiszámításában.

Röviden:

• Di közvetlenül összefoglalja, hogy mennyit változik az összes illesztett érték, ha az i-edik megfigyelést töröljük.
• Egy nagy Di értékű adatpont azt jelzi, hogy az adatpont erősen befolyásolja az illesztett értékeket.

Vizsgáljuk meg, mit is jelent pontosan ez az első állítás néhány példánk kapcsán.

1. példa (ismét). Talán emlékszik, hogy ezeknek az adatoknak a grafikonja (influence1.txt) azt sugallja, hogy ebben a példában nincsenek kiugró és befolyásoló adatpontok:

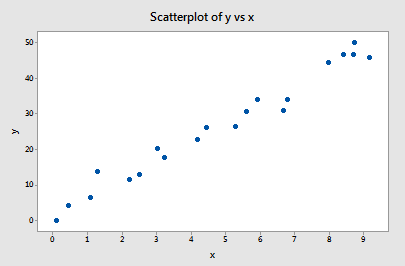
Ha az összes n = 20 adatpont felhasználásával regresszáljuk y-t x-re, akkor megállapítjuk, hogy a becsült metszési együttható b0 = 1,732 és a becsült meredekségi együttható b1 = 5,117. Ha az első adatpontot eltávolítjuk az adathalmazból, és a fennmaradó n = 19 adatpont felhasználásával regresszáljuk az y-t x-re, akkor megállapítjuk, hogy a becsült b0 metszési együttható = 1,732 és a becsült b1 meredekség együttható = 5,1169. Ahogy reméljük és várjuk, a becslések nem változnak olyan nagyon, ha eltávolítjuk az egy adatpontot. Folytatva ezt a folyamatot, amelynek során az egyes adatpontokat egyesével távolítjuk el, és az így kapott becsült meredekségeket (b1) a becsült metszéspontokkal (b0) szemben ábrázoljuk, a következőket kapjuk:

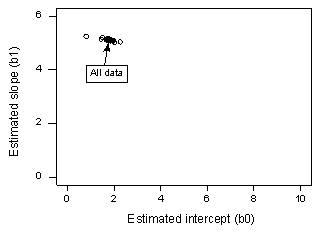
A tömör fekete pont az összes n = 20 adatpont alapján becsült együtthatókat jelöli. A nyitott körök az egyes adatpontok egyenkénti törlésével kapott becsült együtthatókat jelölik. Amint látható, a becsült együtthatók mindegyike összeadódik, függetlenül attól, hogy melyik adatpontot távolítjuk el, ha egyáltalán eltávolítjuk. Ez arra utal, hogy egyetlen adatpont sem befolyásolja indokolatlanul a becsült regressziós függvényt vagy viszont az illesztett értékeket. Ebben az esetben azt várnánk, hogy az összes Cook-féle távolságmérés, Di, kicsi legyen.

4. példa (ismét). Talán emlékszik arra, hogy ezeknek az adatoknak a grafikonja (influence4.txt) azt sugallja, hogy egy adatpont befolyásos és kiugró ebben a példában:

Ha az összes n = 21 adatpont felhasználásával regresszáljuk y-t x-re, akkor megállapítjuk, hogy a becsült intercept együttható b0 = 8,51 és a becsült meredekség együttható b1 = 3,32. Ha a piros adatpontot eltávolítjuk az adathalmazból, és a fennmaradó n = 20 adatpont felhasználásával regresszáljuk y-t x-re, akkor megállapítjuk, hogy a becsült b0 metszési együttható = 1,732 és a becsült b1 meredekségi együttható = 5,1169. Wow-a becslések jelentősen megváltoznak az egy adatpont eltávolításával. Folytatva ezt a folyamatot, amelynek során az egyes adatpontokat egyesével távolítjuk el, és az így kapott becsült meredekségeket (b1) a becsült metszéspontokkal (b0) szemben ábrázoljuk, a következőket kapjuk:

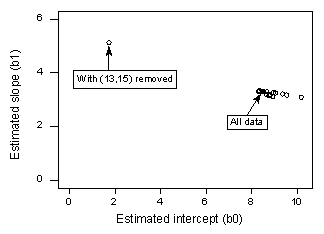
Az egyszínű fekete pont ismét az összes n = 21 adatpont alapján becsült együtthatókat mutatja. A nyitott körök az egyes adatpontok egyenkénti törlésével kapott becsült együtthatókat jelölik. Amint látható, a piros adatpont (x = 13, y = 15) kivételével a becsült együtthatók mind egy csoportba kerülnek, függetlenül attól, hogy melyik adatpontot, ha egyáltalán, eltávolítjuk. Ez arra utal, hogy a piros adatpont az egyetlen olyan adatpont, amely indokolatlanul befolyásolja a becsült regressziós függvényt és ezáltal az illesztett értékeket. Ebben az esetben azt várnánk, hogy a piros adatpontra vonatkozó Cook-féle távolságmérték, Di, nagy, a többi adatpontra vonatkozó Cook-féle távolságmérték, Di, pedig kicsi legyen.

A Cook-féle távolságmértékek használata. A fenti példák szépsége abban rejlik, hogy egyszerű ábrák segítségével láthatjuk, mi történik. Sajnos a többszörös regresszió esetében nem támaszkodhatunk egyszerű ábrákra. Ehelyett iránymutatásokra kell támaszkodnunk annak eldöntéséhez, hogy mikor elég nagy a Cook-féle távolságmérték ahhoz, hogy egy adatpontot befolyásosnak tekintsünk.

Itt vannak az általánosan használt iránymutatások:

• Ha Di nagyobb, mint 0,5, akkor az i-edik adatpont érdemes a további vizsgálatra, mivel befolyásos lehet.
• Ha Di nagyobb, mint 1, akkor az i-edik adatpont nagy valószínűséggel befolyásos.
• Vagy ha Di kiemelkedik a többi Di érték közül, mint egy fájó hüvelykujj, akkor szinte biztosan befolyásos.

2. példa (ismét). Nézzük meg a Cook-féle távolságmérőt erre az adathalmazra (influence2.txt):

Regresszáljuk y-t x-re, és a Cook-féle távolságmértékeket kérve a következő szoftverkimenetet kapjuk:

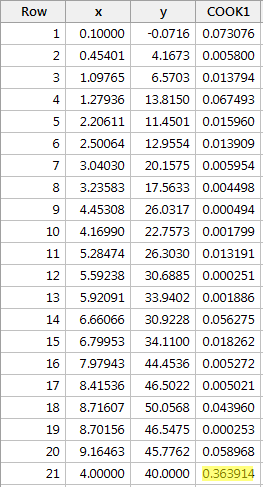
A piros adatpont Cook-féle távolságmértéke (0,363914) kicsit kilóg a többi Cook-féle távolságmértékhez képest. Mégis, a piros adatpont Cook-féle távolságmértéke 0,5-nél kisebb. Ezért a Cook-féle távolságmérték alapján a piros adatpontot nem minősítenénk befolyásosnak.

3. példa (ismét). Nézzük meg a Cook-féle távolságmértéket erre az adathalmazra (influence3.txt):

Regresszáljuk y-t x-re, és a Cook-féle távolságmértékeket kérve a következő szoftverkimenetet kapjuk:

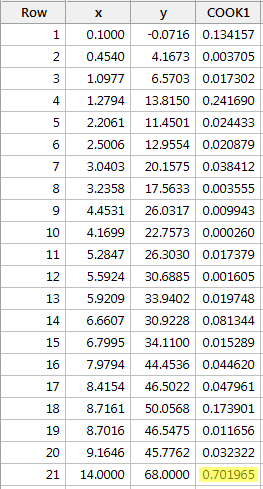
A piros adatpont Cook-féle távolságmértéke (0,701965) kicsit kilóg a többi Cook-féle távolságmértékhez képest. Mégis, a piros adatpont Cook-féle távolságmértéke nagyobb, mint 0,5, de kisebb, mint 1. Ezért a Cook-féle távolságmérték alapján talán tovább vizsgálódnánk, de nem feltétlenül minősítenénk a piros adatpontot befolyásosnak.

4. példa (ismét). Nézzük meg a Cook-féle távolságmérőt erre az adathalmazra (influence4.txt):

Regresszáljuk y-t x-re, és a Cook-féle távolságmérőt kérve a következő szoftverkimenetet kapjuk:

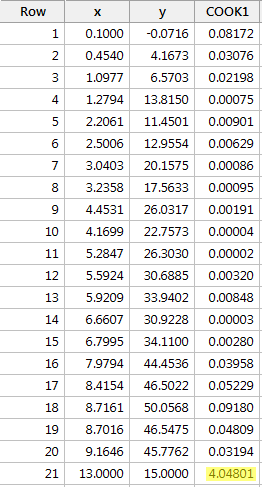
Ez esetben a Cook-féle távolságmérőt a piros adatpontra (4.04801) jelentősen kiemelkedik a többi Cook-féle távolságméréshez képest. Ráadásul a piros adatpont Cook-féle távolságmértéke nagyobb, mint 1. Ezért a Cook-féle távolságmérték alapján – nem meglepő módon – a piros adatpontot befolyásosnak minősítenénk.

A Cook-féle távolság értelmezésének néha használt alternatív módszere az, hogy a mértéket az F(k+1, n-k-1) eloszláshoz viszonyítjuk, és megkeressük a megfelelő percentilis értéket. Ha ez a percentilis kevesebb, mint körülbelül 10 vagy 20 százalék, akkor az esetnek kevés nyilvánvaló hatása van az illesztett értékekre. Ha viszont közel 50 százalékos vagy még magasabb, akkor az esetnek jelentős hatása van. (Bármi, ami a “kettő között” van, kétértelműbb.)