14. rész : Pont- és Hadamard-produktum

A korábban tárgyalt mátrixszorzáson kívül a vektorokat még két módszerrel lehet szorozni: A pontszorzat és a Hadamard-termék. A két módszerrel kapott eredmények különböznek.

Az azonos sorhoz és oszlophoz tartozó elemeket összeszorozzuk, és a termékeket úgy adjuk össze, hogy az eredmény egy skalár legyen.

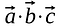
A mátrixszorzással ellentétben a ponttermék eredménye nem egy másik vektor vagy mátrix, hanem skalár.

A vektorok sorrendje nem számít a pontszorzatnál, csak a két vektor elemeinek száma legyen egyenlő.

A pontszorzat geometriai képlete

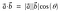
A pontszorzatot belső szorzatnak vagy skaláris szorzatnak is nevezik.

Vektor projekciója

Tegyük fel, hogy van két c és d vektorunk, melyeket phi(Ф) szöggel metszünk.

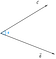
Most, a c vektor d vektorra való vetülete a következőképpen ábrázolható

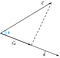
Az ábrából következtethetünk arra, hogy a vetület egyenlő a c vektor phi(Ф) szögre vonatkoztatott vízszintes komponensével.

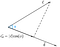
Ezt nevezzük skalárvetítésnek.Ahhoz, hogy megtaláljuk a c vektor d vektorra való vektorvetületét, meg kell szoroznunk a skalárvetületet a d egységvektorral.

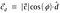
A d egységvektor értékének behelyettesítésével.

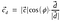
Így, a pontszorzatot így is ábrázolhatjuk:

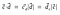
A vetületeket széles körben használják a lineáris algebrában és a gépi tanulásban (a Support Vector Machine(SVM) egy gépi tanulási algoritmus, amelyet adatok osztályozására használnak).

Hadamard-termék (elemenkénti szorzás)

A két vektoradagolás nagyon hasonlít a mátrixadagoláshoz, az adott vektorok/mátrixok azonos sorainak és oszlopainak megfelelő elemeket összeszorozzuk, hogy egy új vektort/mátrixot kapjunk.

A francia matematikusról, Jacques Hadamardról kapta a nevét.

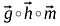
A szorzandó mátrixok/vektorok sorrendjének azonosnak kell lennie, és a kapott mátrix is azonos sorrendű lesz.

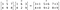
Hadamard-terméket a képtömörítési eljárásokban, például a JPEG-ben használják. Schur-terméknek is nevezik a német matematikus, Issai Schur után.

Hadamard-terméket a rekurrens neurális hálózatok (RNN) LSTM (Long Short-Term Memory) celláiban használják.