Helmholtz-Resonanz
- Analyse der Helmholtz-Resonanz
- Resonanz, Impedanz, Phasen- und Frequenzabhängigkeit
- Komplikationen mit der Länge
- Helmholtz-Resonanzen und Gitarren
Analyse der Helmholtz-Resonanz
Kommen wir nun zur Quantität: Zunächst einmal nehmen wir an, dass die Wellenlänge des erzeugten Schalls viel größer ist als die Abmessungen des Resonators. Für die Flaschen in der Animation oben auf dieser Seite betragen die Wellenlängen 180 bzw. 74 cm. Diese Näherung ist also ziemlich gut, aber es lohnt sich, sie zu überprüfen, wenn man etwas als Helmholtz-Oszillator beschreiben will. Die Folge dieser Näherung ist, dass wir Druckschwankungen innerhalb des Volumens des Behälters vernachlässigen können: die Druckschwingung hat überall im Behälter die gleiche Phase.
Die Luft im Hals hat eine effektive Länge L und eine Querschnittsfläche S. Ihre Masse ist dann SL mal die Dichte der Luft ρ. (Einige Komplikationen bezüglich der effektiven Länge werden am Ende dieser Seite diskutiert.) Wenn dieser „Luftpfropfen“ eine kleine Strecke x in die Flasche hinabsteigt, komprimiert er die Luft im Behälter, so dass die Luft, die zuvor das Volumen V einnahm, nun das Volumen V – Sx hat. Folglich steigt der Druck dieser Luft vom atmosphärischen Druck PA auf einen höheren Wert PA + p.
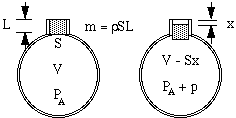
Nun könnte man meinen, dass die Druckerhöhung einfach proportional zur Volumenverringerung ist. Das wäre der Fall, wenn die Kompression so langsam abliefe, dass sich die Temperatur nicht ändert. Bei Schwingungen, die zu Schall führen, sind die Veränderungen jedoch schnell, so dass die Temperatur bei der Kompression ansteigt, was zu einer größeren Druckänderung führt. Technisch gesehen handelt es sich um adiabatische Vorgänge, d. h. die Wärme hat keine Zeit, sich zu bewegen, und die sich daraus ergebende Gleichung beinhaltet eine Konstante γ, das Verhältnis der spezifischen Wärme, das für Luft etwa 1,4 beträgt. (Dies wird in einem Anhang erklärt.) Folglich ist die Druckänderung p, die durch eine kleine Volumenänderung ΔV erzeugt wird, nur
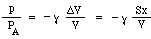
Jetzt wird die Masse m durch den Druckunterschied zwischen dem oberen und unteren Teil des Halses bewegt, d.h. eine Nettokraft pS, so dass wir das Newtonsche Gesetz für die Beschleunigung a schreiben:
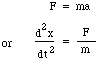
Ersetzen von F und m ergibt: 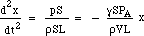
Die Rückstellkraft ist also proportional zur Verschiebung. Dies ist die Bedingung für die einfache harmonische Bewegung, und sie hat eine Frequenz, die 1/2π mal die Quadratwurzel der Proportionalitätskonstante ist, also
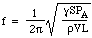
Nun wird die Schallgeschwindigkeit c in Luft durch die Dichte, den Druck und das Verhältnis der spezifischen Wärme bestimmt, so dass wir schreiben können:
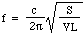
Ein paar Zahlen: für eine 1-Liter-Flasche mit S = 3 Quadratzentimetern und L = 5 Zentimetern beträgt die Frequenz 130 Hz, das ist etwa das C unter dem mittleren C. (Siehe Anmerkungen.) Die Wellenlänge beträgt also 2,6 Meter, was viel größer ist als die Flasche. Dies rechtfertigt, post hoc, die zu Beginn der Herleitung gemachte Vermutung.
Resonanz, Impedanz, Phasen- und Frequenzabhängigkeit
Dieser Abschnitt kann für sich allein gelesen werden, aber wenn Sie detailliertere Hintergrundinformationen wünschen, lesen Sie bitte Oszillationen, erzwungene Oszillationen und akustische Nachgiebigkeit, Trägheit und Impedanz.
Kehren wir zur mechanischen Darstellung zurück und betrachten wir den Helmholtz-Resonator von außen, wie im ersten Schema gezeigt: Wir drücken mit einer oszillierenden Kraft F mit der Frequenz f auf die Masse m (die Luft im Hals des Resonators), die sich auf der Feder (die eingeschlossene Luft) mit der Federkonstante k abstützt, deren anderes Ende fest ist (die Luft im Resonator kann nicht entweichen). Unrealistischerweise vernachlässigen wir die Schwerkraft und die Reibung (vorerst).
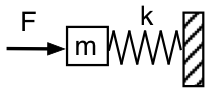
Die zur Beschleunigung der Masse erforderliche Kraft ist proportional zur Beschleunigung und damit proportional zu f2. Bei hinreichend niedriger Frequenz ist die zur Beschleunigung der Masse erforderliche Kraft vernachlässigbar, so dass F die Feder nur zusammendrücken und ausdehnen muss. In diesem Grenzfall ist die angewandte Kraft F = +kx. (Die Federkraft ist -kx.) Die mechanische Impedanz des Systems bei dieser niedrigen Frequenz ist nachgiebig oder federartig. Akustisch sieht es wie eine akustische Nachgiebigkeit aus: Wir drücken die Luftmasse im Hals und komprimieren die Luft im Resonator. Die nach rechts wirkende Kraft F ist phasengleich mit dem nach rechts gemessenen x, liegt also 90° hinter der Geschwindigkeit und der angelegte Druck 90° hinter dem akustischen Fluss in den Resonator.
Erinnern Sie sich an die f2-Abhängigkeit der Beschleunigung. Bei einer ausreichend hohen Frequenz ist die Federkraft also vernachlässigbar im Vergleich zu derjenigen, die die Masse beschleunigt. F ist also gleichphasig mit der Beschleunigung und liegt damit 90° vor der Geschwindigkeit. Akustisch gesehen ist der angelegte Druck dem akustischen Fluss in den Resonator um 90° voraus. Es handelt sich um eine mechanische oder akustische Trägheit.
Bei der Resonanzfrequenz (ich spreche immer noch von der obigen Skizze) kann die Amplitude bei einer sehr kleinen Kraft sehr groß sein. Bei Resonanz ist die Impedanz also sehr gering, wenn man die Kraft betrachtet, die von außen auf die Masse wirkt (obiges Diagramm). Bei Resonanz gibt es einen maximalen Fluss in den und aus dem Resonator.
Betrachten wir nun, was passiert, wenn wir den Druck im Inneren des Resonators (weg vom Hals) betrachten. Hier betrachten wir die Kraft auf die Feder, also sieht unser mechanisches Analogon wie dieses Schema aus.
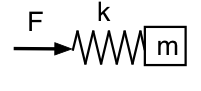
Diesmal bedeutet die niedrige Frequenz, dass die Kraft bei einer gegebenen Amplitude klein sein kann: Die Feder und die Masse bewegen sich zusammen als eine Masse, und das System sieht diesmal bei niedriger Frequenz träge aus. Bei hoher Frequenz bewegt sich die Masse kaum, und das System ist federartig oder nachgiebig. Die Phasenbeziehungen sind also entgegengesetzt zu dem, was wir vorher hatten: bei niedrigem f eilt p U um 90° voraus; bei hohem f eilt p U um 90° hinterher.
Komplikationen mit der effektiven Länge
Das erste Diagramm auf dieser Seite zeichnet den „Stöpsel“ der Luft so, als ob er ein Zylinder wäre, der an beiden Enden des Flaschenhalses sauber endet. Das ist stark vereinfacht. In der Praxis bewegt sich ein zusätzliches Volumen sowohl innen als auch außen mit der Luft im Hals – wie in der obigen Animation angedeutet. Die zusätzliche Länge, die zur geometrischen Länge des Halses hinzugefügt werden sollte, beträgt typischerweise (und sehr ungefähr) das 0,6-fache des Radius am äußeren Ende und einen Radius am inneren Ende).
|
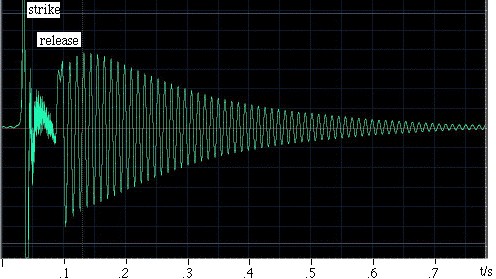
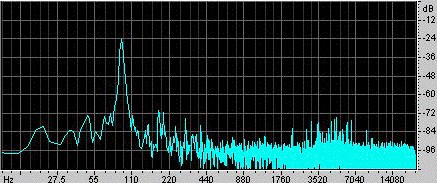
Ein Beispiel. Ra Inta hat dieses Beispiel gemacht. Er nahm einen kugelförmigen Helmholtz-Resonator mit einem Volumen von 0,00292 m3 und einem zylindrischen Hals von 0,080 m Länge und 0,00083 m2 Querschnittsfläche. Um ihn anzuregen, schlug er ihn mit der Handfläche an und ließ ihn dann los. Ein Mikrofon im Inneren des Resonators zeichnet den Schall auf, der im Oszillogramm links dargestellt ist. Man sieht, dass die Hand den Resonator für etwas weniger als 0,1 s abdichtet und dass die Schwingungen während dieser Zeit schwächer und relativ hochfrequent sind. Wenn die Hand losgelassen wird, entsteht eine Schwingung, die allmählich abklingt, da sie durch viskosen und turbulenten Widerstand sowie durch Schallabstrahlung Energie verliert. Bei näherer Betrachtung zeigt sich, dass die Frequenz leicht ansteigt, wenn sich die Hand vom offenen Ende entfernt, weil dadurch der Raumwinkel, der für die Abstrahlung zur Verfügung steht, durch die Hand eingeschränkt wird und somit der Endeffekt (oder die Endkorrektur) zunimmt. Die Länge des Halses vergrößert sich um einen schallgedämpften und einen nicht schallgedämpften Endeffekt, so dass sich eine effektive Länge von 0,105 m ergibt. Bei einer Schallgeschwindigkeit von 343 m/s ergibt der obige Ausdruck eine Resonanzfrequenz von 90 Hz. |
|
Helmholtz-Resonanzen und Gitarren
* Ich habe oben gesagt, dass die Luft im Korpus einer Gitarre fast wie ein Helmholtz-Oszillator wirkt. Dieser Fall ist kompliziert, weil der Korpus ein wenig anschwellen kann, wenn der Luftdruck im Inneren ansteigt – und auch, weil die Luft „im“ Schallloch der Gitarre eine Geometrie hat, die man sich nicht so leicht vorstellen kann wie die im Hals einer Flasche. Im Fall des Gitarrenkorpus entspricht die Länge des Luftpfropfens in etwa den beiden „Endeffekten“ am Ende eines „Rohrs“, das nur ein paar mm dick ist. Die Endstücke stehen jedoch im Verhältnis zum Radius des Lochs und haben eine ähnliche Größe wie dieses, so dass die Luftmasse erheblich ist. Die Länge des Endeffekts eines zylindrischen Rohrs, das in eine unendliche, ebene Schallwand mündet, beträgt das 0,85-fache des Radius des Rohrs. Obwohl der Resonanzboden einer Gitarre nicht unendlich ist, würde man einen ähnlichen Endeffekt erwarten, so dass die effektive Länge des Luftpfropfens“ etwa das 1,7-fache des Radius des Lochs betragen würde. (Manche Hersteller erhöhen diesen Wert, indem sie ein kurzes Rohr mit gleichem Radius unter dem Schallloch anbringen.)
Ein paar Leute haben geschrieben und gefragt, wie groß das Schallloch für ein bestimmtes Instrument sein sollte. Nun, wir können die obige Gleichung verwenden, um diese Frage zu beantworten. Allerdings ist die Schwellung des Korpus wichtig. Dadurch wird die „Feder“ der Luft etwas weicher, und die Frequenz sinkt. Die reine Helmholtz-Resonanz kann untersucht werden, indem das Volumen des Körpers konstant gehalten wird. Bei dieser Messung wird die Gitarre üblicherweise in Sand eingegraben, um das Anschwellen oder „Atmen“ des Korpus zu verhindern. Allerdings werden Gitarren in der Regel nicht in dieser Situation gespielt. Daher wird die Helmholtz-Berechnung eine Überschätzung der Resonanzfrequenz für einen echten, flexiblen Korpus ergeben.
Nehmen wir ein kreisförmiges Schallloch mit dem Radius r an, also S = πr2 und L = 1,7r wie oben erklärt. Wenn wir in die Gleichung für die Helmholtz-Frequenz mit c = 340 m/s einsetzen, erhalten wir:
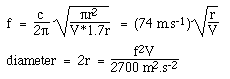
Beachten Sie, dass wir SI-Standardeinheiten verwenden: Wir haben die Schallgeschwindigkeit in Metern und Sekunden angegeben, also muss das Volumen in Kubikmetern und die Frequenz in Hertz sein, um eine Antwort in Metern zu erhalten.
Komplizierter wird es, wenn die Tonlöcher nicht kreisförmig sind, weil der Endeffekt nicht dem eines Kreises mit der gleichen Fläche entspricht. Der Doktorand und Geigenbauer John McLennan schreibt gerade einen Bericht über einige Messungen zu diesem Thema, den wir hier bald veröffentlichen werden.
Bei Instrumenten der Gitarren- und Geigenfamilie liegt die Helmholtz-Resonanz (plus Korpusresonanz) oft in der Nähe oder etwas unterhalb der Frequenz der zweittiefsten Saite, etwa bei D auf einer Geige oder G-A auf einer Gitarre. Sie können die Helmholtz-Frequenz erheblich reduzieren oder verschieben, indem Sie das Loch ganz oder teilweise mit einem passend geformten Stück steifer Pappe abdecken. Wenn du dann einen Ton in der Nähe der Resonanz spielst und dann die Pappe so verschiebst, dass sie das Loch abwechselnd verdeckt und freigibt, wirst du die Wirkung der Resonanz deutlich hören.
Ist der 0,85r-Effekt sinnvoll? Ra Inta, der in unserem Labor über Gitarrenakustik promoviert hat, schlägt eine interessante Demonstration vor:
Dämpfen Sie die Saiten Ihrer Gitarre, damit sie nicht schwingen (z. B. ein Taschentuch zwischen Saiten und Griffbrett). Halten Sie die Handfläche einer Hand über das Schallloch und nahe daran. Schlagen Sie mit einem Finger der anderen Hand in der Nähe des Schalllochs und in der Nähe der ersten Saite kräftig auf die Decke. Sie werden einen Luftimpuls auf Ihrer Handfläche spüren. Der Schlag Ihres Fingers drückt den Resonanzboden nach innen und drückt etwas Luft aus dem Korpus. Bewegen Sie nun Ihre Hand allmählich weiter vom Loch weg und klopfen Sie weiter mit dem Finger. Wann hören Sie auf, die Bewegung der Luft zu spüren? So erhältst du eine ungefähre Einschätzung der Länge des „Endeffekts“ im Falle des Schalllochs.
Tuning der Helmholtz-Resonanz
Unter den Veröffentlichungen von John McLennan, einem Doktoranden in diesem Labor, befindet sich ein Artikel, in dem er die Helmholtz-Resonanz durch Variation der Schallgeschwindigkeit variiert.
- McLennan, J.E. (2003) „A0- und A1-Studien an der Violine mit CO2-, He- und Luft/Helium-Gemischen“. Acustica, 89, 176-180.
Einige Bilder von historischen Helmholtz-Resonatoren, zur Verfügung gestellt von Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply