Greensche Funktion

Generell gesprochen, ist eine Greensche Funktion ein Integralkern, der zur Lösung von Differentialgleichungen aus einer Vielzahl von Familien verwendet werden kann, darunter einfachere Beispiele wie gewöhnliche Differentialgleichungen mit Anfangs- oder Randwertbedingungen sowie schwierigere Beispiele wie inhomogene partielle Differentialgleichungen (PDE) mit Randbedingungen. Green-Funktionen sind aus mehreren Gründen wichtig: Sie ermöglichen eine visuelle Interpretation der mit einer Kraftquelle oder einer in einem Punkt konzentrierten Ladung verbundenen Aktionen (Qin 2014), was sie in Bereichen der angewandten Mathematik besonders nützlich macht. Insbesondere die Methoden der Green’schen Funktionen werden häufig verwendet, z. B. in der, Physik und im Ingenieurwesen eingesetzt.

Gegenüber einem linearen Differentialoperator , der auf die Sammlung von Verteilungen über einer Teilmenge eines euklidischen Raums wirkt, wird eine Greensche Funktion in dem Punkt , der entspricht, eine beliebige Lösung von

(1)

wobei die Deltafunktion bezeichnet. Die Motivation für die Definition einer solchen Funktion ist weit verbreitet, aber wenn man die obige Identität mit einer Funktion multipliziert und in Bezug auf integriert, erhält man

(2)

Die rechte Seite reduziert sich aufgrund der Eigenschaften der Deltafunktion lediglich auf , und weil ein linearer Operator ist, der nur auf und nicht auf wirkt, kann die linke Seite umgeschrieben werden als

(3)

Diese Reduktion ist besonders nützlich beim Lösen von in Differentialgleichungen der Form

(4)

wobei die obige Arithmetik bestätigt, dass

(5)

und woraus folgt, dass die spezifische Integralform

(6)

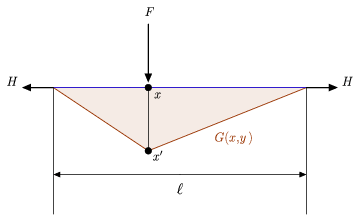
Die obige Abbildung veranschaulicht sowohl die intuitive physikalische Interpretation einer Greenschen Funktion als auch eine relativ einfache zugehörige Differentialgleichung, mit der man die obige Definition vergleichen kann (Hartmann 2013). Sie zeigt insbesondere ein gespanntes Seil der Länge , das zwischen zwei Wänden aufgehängt ist und durch eine identische horizontale Kraft , die auf jedes seiner Enden ausgeübt wird, und eine seitliche Last , die an einem inneren Punkt auf dem Seil platziert ist, in Position gehalten wird. Nehmen wir an, dass der Punkt ist, der auf dem abgelenkten Seil entspricht, dass die nach unten gerichtete Kraft konstant ist, sagen wir , und dass die Ablenkung des Seils bezeichnet. Diesem physikalischen System entspricht die Differentialgleichung

(7)

für mit , ein System, dessen Einfachheit es erlaubt, sowohl seine Lösung als auch seine Greensche Funktion explizit zu schreiben:

(8)

und

(9)

jeweils. Wie in der obigen Abbildung gezeigt, hat das verschobene Seil das stückweise lineare Format, das durch gegeben ist, was die Behauptung bestätigt, dass die Greensche Funktion , die diesem System zugeordnet ist, die Wirkung des horizontalen Seils darstellt, die der Anwendung einer Kraft entspricht.

Eine Greensche Funktion, die ein Paar von Argumenten annimmt, wird manchmal als Zwei-Punkt Greensche Funktion bezeichnet. Dies steht im Gegensatz zu Mehrpunkt-Green-Funktionen, die im Bereich der Vielteilchentheorie von besonderer Bedeutung sind.

Als elementares Beispiel für eine Zweipunktfunktion im obigen Sinne sei das Problem der Bestimmung des Potentials betrachtet, das von einer Ladungsverteilung erzeugt wird, deren Ladungsdichte ist, wobei die Anwendung der Poisson’schen Gleichung und des Coulomb’schen Gesetzes auf das Potential bei , das von jedem Element der Ladung erzeugt wird, eine Lösung

(10)

woraus folgt, unter bestimmten Bedingungen für den Bereich gilt, in dem . Da die rechte Seite als ein Integraloperator betrachtet werden kann, der in umwandelt, kann man diese Lösung in Form einer Greenschen Funktion mit der Form

(11)

wobei die Lösung umgeschrieben werden kann:

(12)

(Arfken 2012).

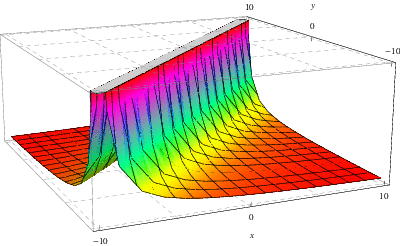
Die obige Abbildung zeigt die Green’sche Funktion, die mit der Lösung der –-Gleichung verbunden ist, die hier besprochen wurde, und , bzw. , auf der -, bzw. -, Achse aufgetragen ist.

Eine einigermaßen umfassende Liste von Green’schen Funktionen, die verschiedenen Differentialgleichungen entsprechen, wird online von Kevin Cole (Cole 2000) geführt.

Durch die Vielzahl der Literatur, die über Green’sche Funktionen geschrieben wurde, können verschiedene Notationen und Definitionen auftauchen, von denen sich einige thematisch von den oben genannten unterscheiden, die aber im Allgemeinen die wichtigen Eigenschaften der Ergebnisse nicht beeinflussen. Wie das obige Beispiel zeigt, ziehen es einige Autoren vor, die Variablen und als Vektoren und zu bezeichnen, um die Tatsache zu betonen, dass sie Elemente von für einige sind, die größer als 1 sein können (Arfken 1985). Es ist auch relativ üblich, die Definition mit einem negativen Vorzeichen zu sehen, so dass als die Funktion definiert ist, für die

(13)

aber da diese rein physikalische Betrachtung keine Auswirkung auf die zugrunde liegende Mathematik hat, wird dieser Gesichtspunkt im Allgemeinen übersehen. Es sind auch verschiedene andere Schreibweisen für eine Green’sche Funktion bekannt, darunter die Verwendung eines kleingeschriebenen anstelle von (Stakgold 1979) sowie die Einfügung eines senkrechten Strichs anstelle eines Kommas, z. B., (Duffy 2001).

In anderen Fällen finden sich in der Literatur Definitionen, die eng mit den Kontexten verbunden sind, in denen sie präsentiert werden. Zum Beispiel definieren einige Autoren Green’sche Funktionen als Funktionen, die einen bestimmten Satz von Bedingungen erfüllen, z.B. die Existenz auf einer speziellen Art von Domäne, die Verbindung mit einem ganz bestimmten Differentialoperator oder die Erfüllung eines präzisen Satzes von Randbedingungen. Eines der gebräuchlichsten Beispiele dieser Art findet sich in den Aufzeichnungen von z.B., Speck, wo eine Greensche Funktion so definiert ist, dass sie für Punkte und für alle Punkte erfüllt, die im Randbereich von liegen (Speck 2011). Diese spezielle Definition stellt einen integralen Kern dar, der der Lösung einer verallgemeinerten Poisson-Gleichung entspricht und würde daher bei einer Anpassung an ein allgemeineres Umfeld auf offensichtliche Einschränkungen stoßen. Andererseits sind solche Beispiele auch nicht ohne Vorteile. Im Fall des obigen verallgemeinerten Poisson-Beispiels kann zum Beispiel jede solche Green’sche Funktion so aufgeteilt werden, dass

(14)

wobei und für den regulären Laplacian (Hartman 2013). In solchen Situationen wird als fundamentale Lösung der zugrundeliegenden Differentialgleichung und als deren reguläre Lösung bezeichnet; als solche werden und manchmal als fundamentale bzw. reguläre Teile von bezeichnet.

Einige grundlegende Eigenschaften einer allgemeinen Green’schen Funktion ergeben sich unmittelbar (oder fast unmittelbar) aus ihrer Definition und sind auf alle besonderen Fälle übertragbar. Wenn zum Beispiel der Kern des Operators nicht trivial ist, dann kann es mehrere Green’sche Funktionen geben, die zu einem einzigen Operator gehören; deshalb muss man vorsichtig sein, wenn man sich auf „die“ Green’sche Funktion bezieht. Greensche Funktionen erfüllen eine adjungierte Symmetrie in ihren beiden Argumenten, so dass

(15)

wobei hier als die Lösung der Gleichung

(16)

Hier ist der Adjunkt von . Eine unmittelbare Folgerung aus dieser Tatsache ist, dass für selbstadjungierte Operatoren , symmetrisch ist:

(17)

Diese Identität wird oft als Reziprozitätsprinzip bezeichnet und besagt in physikalischer Hinsicht, dass die Reaktion bei , die durch eine Einheitsquelle bei verursacht wird, dieselbe ist wie die Reaktion bei aufgrund einer Einheitskraft bei (Stakgold 1979).

Die wesentliche Eigenschaft jeder Green’schen Funktion ist, dass sie eine Möglichkeit bietet, die Antwort einer beliebigen Differentialgleichungslösung auf eine Art von Quellterm in Gegenwart einer Reihe von Randbedingungen zu beschreiben (Arfken et al. 2012). Einige Autoren sind der Ansicht, dass eine Green’sche Funktion in der Theorie partieller Differentialgleichungen in etwa die gleiche Rolle spielt wie Fourier-Reihen bei der Lösung gewöhnlicher Differentialgleichungen (Mikula und Kos 2006).

Für abstraktere Szenarien gibt es eine Reihe von Konzepten, die als kontextspezifische Analoga zum Begriff der Green’schen Funktion dienen. Zum Beispiel ist es in der Funktionsanalyse oft nützlich, eine so genannte verallgemeinerte Greensche Funktion zu betrachten, die viele analoge Eigenschaften hat, wenn sie abstrakt gegen Funktionale statt gegen Funktionen integriert wird. Solche Verallgemeinerungen haben in der Tat einen völlig analogen Zweig der theoretischen PDE-Analyse hervorgebracht und stehen selbst im Mittelpunkt zahlreicher Forschungsarbeiten.