Articles /

Gram-Schmidt-Verfahren

von Marco Taboga, PhD

Das Gram-Schmidt-Verfahren (oder Verfahren) ist eine Folge von Operationen, die es ermöglichen, eine Menge linear unabhängiger Vektoren in eine Menge orthonormaler Vektoren umzuwandeln, die denselben Raum aufspannen wie die ursprüngliche Menge.

Inhaltsverzeichnis

Vorüberlegungen

Wir wollen einige Begriffe wiederholen, die für das Verständnis des Gram-Schmidt-Verfahrens wesentlich sind.

Erinnern wir uns daran, dass zwei Vektoren $r$ und $s$ dann und nur dann orthogonal sind, wenn ihr inneres Produkt gleich Null ist, d.h.

Bei einem inneren Produkt können wir die Norm (Länge) eines Vektors $s$ wie folgt definieren:

Eine Menge von Vektoren heißt dann und nur dann orthonormal, wenn ihre Elemente eine Einheitsnorm haben und orthogonal zueinander sind. Mit anderen Worten, eine Menge von K Vektoren ist orthonormal, wenn und nur wenn

Wir haben bewiesen, dass die Vektoren einer orthonormalen Menge linear unabhängig sind.

Wenn eine Basis für einen Vektorraum auch eine orthonormale Menge ist, nennt man sie eine orthonormale Basis.

Projektionen auf orthonormale Mengen

Im Gram-Schmidt-Verfahren verwenden wir immer wieder den folgenden Satz, der zeigt, dass jeder Vektor in zwei Teile zerlegt werden kann: 1) seine Projektion auf eine orthonormale Menge und 2) einen Rest, der orthogonal zu der gegebenen orthonormalen Menge ist.

Vermutung Sei $S$ ein Vektorraum mit einem inneren Produkt . Sei eine orthonormale Menge. Für jedes $sin S$ haben wir, wobei $arepsilon _{S}$ orthogonal zu $u_{k}$ für jedes $k=1,ldots ,K ist.$

Beweis

DefineDann haben wir für jedes $j=1,ldots ,K$, dasswo: In den Schritten $Rahmen{A}$ und $Rahmen{B}$ haben wir die Tatsache benutzt, dass das innere Produkt in seinem ersten Argument linear ist; im Schritt $rame{C}$ haben wir die Tatsache benutzt, dass wenn $keq j$, da wir es mit einer orthonormalen Menge zu tun haben; im Schritt $rame{D}$ haben wir die Tatsache benutzt, dass die Norm von $u_{j}$ gleich 1 ist. Daher ist $arepsilon _{S}$, wie oben definiert, orthogonal zu allen Elementen der orthonormalen Menge, was den Satz beweist.

Der Term wird die lineare Projektion von $s$ auf die orthonormale Menge genannt, während der Term $arepsilon _{S}$ das Residuum der linearen Projektion heißt.

Normalisierung

Eine weitere vielleicht offensichtliche Tatsache, die wir im Gram-Schmidt-Verfahren immer wieder verwenden werden, ist, dass, wenn wir einen beliebigen Nicht-Null-Vektor nehmen und ihn durch seine Norm dividieren, das Ergebnis der Division ein neuer Vektor ist, der eine Einheitsnorm hat.

Mit anderen Worten, wenn , dann haben wir durch die Definitheitseigenschaft der Norm, dass

Als Konsequenz können wir definieren und durch die Positivität und absolute Homogenität der Norm, haben wir

Überblick über das Verfahren

Nachdem wir nun wissen, wie man einen Vektor normalisiert und wie man ihn in eine Projektion auf eine orthonormale Menge und einen Rest zerlegt, können wir das Gram-Schmidt-Verfahren erklären.

Wir werden einen Überblick über das Verfahren geben, danach werden wir es formal als Satz ausdrücken und wir werden alle technischen Details im Beweis des Satzes diskutieren.

Hier ist der Überblick.

Wir haben eine Menge linear unabhängiger Vektoren .

Um den Prozess zu beginnen, normalisieren wir den ersten Vektor, d.h. wir definieren

Im zweiten Schritt projizieren wir $s_{2}$ auf $u_{1}$:wobei $arepsilon _{2}$ das Residuum der Projektion ist.

Dann normalisieren wir das Residuum:

Wir werden später beweisen, dass (damit die Normalisierung durchgeführt werden kann), weil die Ausgangsvektoren linear unabhängig sind.

Die beiden so erhaltenen Vektoren $u_{1}$ und $u_{2}$ sind orthonormal.

Im dritten Schritt projizieren wir $s_{3}$ auf $u_{1}$ und $u_{2}$:und wir berechnen das Residuum der Projektion $arepsilon _{3}$.

Dann normalisieren wir es:

Wir fahren auf diese Weise fort, bis wir das letzte normalisierte Residuum $u_{K} $ erhalten.

Am Ende des Prozesses bilden die Vektoren eine orthonormale Menge, weil:

  1. sie das Ergebnis einer Normalisierung sind und folglich eine Einheitsnorm haben;

  2. jedes $u_{k}$ wird aus einem Rest erhalten, der die Eigenschaft hat, orthogonal zu zu sein.

Um diesen Überblick zu vervollständigen, sei daran erinnert, dass die lineare Spannweite von die Menge aller Vektoren ist, die als Linearkombinationen von geschrieben werden können; sie wird mit bezeichnet und ist ein linearer Raum.

Da die Vektoren linear unabhängige Kombinationen von sind, kann jeder Vektor, der als Linearkombination von geschrieben werden kann, auch als Linearkombination von geschrieben werden. Daher stimmen die Spannweiten der beiden Vektormengen überein:

Formale Aussage

Wir formalisieren hier das Gram-Schmidt-Verfahren als einen Satz, dessen Beweis alle technischen Details des Verfahrens enthält.

Vorstellung Sei $S$ ein Vektorraum mit einem inneren Produkt . Seien linear unabhängige Vektoren. Dann gibt es eine Menge von orthonormalen Vektoren , so dassfür jede $kleq K$.

Beweis

Der Beweis erfolgt durch Induktion: Zuerst beweisen wir, dass der Satz für $k=1$ wahr ist, und dann beweisen wir, dass er für ein allgemeines k wahr ist, wenn er für $k-1$ gilt. Wenn $k=1$, hat der Vektor eine Einheitsnorm und bildet für sich selbst eine orthonormale Menge: Es gibt keine anderen Vektoren, so dass die Orthogonalitätsbedingung trivialerweise erfüllt ist. Die Mengeist die Menge aller skalaren Vielfachen von $s_{1}$, die auch skalare Vielfache von $u_{1}$ sind (und umgekehrt). Daher Nehmen wir nun an, dass der Satz für $k-1$ wahr ist. Dann können wir $s_{k}$ auf : projizieren, wobei der Rest $arepsilon _{k}$ orthogonal zu ist. Nehmen wir an, dass $arepsilon _{k}=0$. Dann,Da durch die Annahme für jede $jleq k-1$, haben wir, dass für jede $jleq k-1$, wobei $lpha _{jl}$ Skalare sind. Deshalb,mit anderen Worten, die Annahme, dass $arepsilon _{k}=0$ ist, führt zu dem Schluss, dass $s_{k}$ eine Linearkombination von ist. Das ist aber unmöglich, weil eine der Annahmen des Satzes ist, dass linear unabhängig sind. Daraus folgt, dass sein muss. Wir können also das Residuum normalisieren und den Vektor definieren, der eine Einheitsnorm hat. Wir wissen bereits, dass $arepsilon _{k}$ orthogonal zu ist. Dies impliziert, dass auch $u_{k}$ orthogonal zu ist. Somit ist eine orthonormale Menge. Nehmen wir nun einen beliebigen Vektor $sin S$, der als geschrieben werden kann, wobei Skalare sind. Da wir durch die Annahme haben, dass Gleichung (2) auch als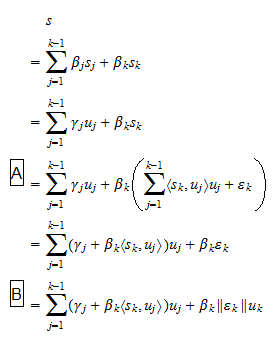geschrieben werden kann, wobei Skalare sind, und: im Schritt $Rahmen{A}$ haben wir Gleichung (1) verwendet; im Schritt $Rahmen{B}$ haben wir die Definition von $u_{k}$ verwendet. Damit haben wir bewiesen, dass jeder Vektor, der als Linearkombination von geschrieben werden kann, auch als Linearkombination von geschrieben werden kann. Die Annahme (3) erlaubt es, die Umkehrung in völlig analoger Weise zu beweisen: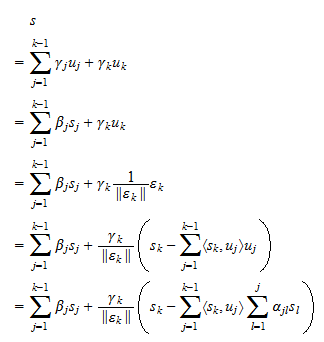Mit anderen Worten: Jede Linearkombination von ist auch eine Linearkombination von . Dies beweist, dass und schließt den Beweis ab.

Jeder Raum mit innerem Produkt hat eine orthonormale Basis

Der folgende Satz stellt eine wichtige Konsequenz des Gram-Schmidt-Verfahrens dar.

Vorschlag Sei $S$ ein Vektorraum mit einem inneren Produkt . Wenn $S$ endliche Dimension hat, dann gibt es eine Orthonormalbasis für $S$.

Beweis

Da $S$ endlich-dimensional ist, gibt es mindestens eine Basis für $S$, bestehend aus K Vektoren . Wir können das Gram-Schmidt-Verfahren auf die Basis anwenden und erhalten eine orthonormale Menge . Da eine Basis ist, erstreckt sie sich über $S$. Daher 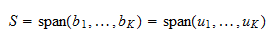ist eine Orthonormalbasis von $S$.

Gelöste Aufgaben

Nachfolgend finden Sie einige Aufgaben mit erklärten Lösungen.

Übung 1

Betrachten Sie den Raum $S$ aller $3mal 1$ Vektoren mit reellen Einträgen und dem inneren Produktwobei $r,sin S$ und $s^{op }$ die Transponierte von $s$ ist. Definiere den Vektor

Normalisiere $s$.

Lösung

Die Norm von $s$ istDaher, ist die Normierung von $s$

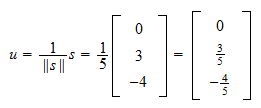
Übung 2

Betrachten Sie den Raum $S$ aller $2mal 1$ Vektoren mit reellen Einträgen und dem inneren Produktwobei $r,sin S$ . Betrachte die beiden linear unabhängigen Vektoren

Transformiere sie mit Hilfe des Gram-Schmidt-Verfahrens in eine orthonormale Menge.

Lösung

Die Norm von $s_{1}$ ist Daher, ist der erste orthonormale VektorDas innere Produkt von $s_{2}$ und $u_{1}$ ist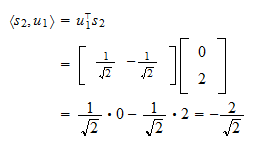Die Projektion von $s_{2}$ auf $u_{1}$ ist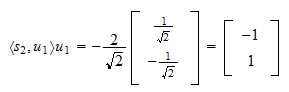Das Residuum der Projektion ist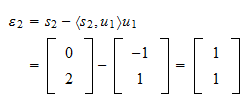Die Norm des Residuums istund das normierte Residuum istDas heißt, ist die gesuchte orthonormale Menge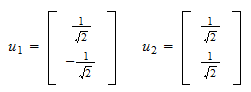

Zitierweise

Bitte zitieren als:

Taboga, Marco (2017). „Gram-Schmidt-Prozess“, Vorlesungen zur Matrixalgebra. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply