Gibbs Sampling

Wir wissen nicht, wie man aus letzterer direkt eine Stichprobe zieht. Aus mathematischer Bequemlichkeit oder vielleicht auch nur aus purem Glück kennen wir jedoch die bedingten Wahrscheinlichkeiten.

Hier kommt das Gibbs Sampling ins Spiel. Gibbs Sampling ist anwendbar, wenn die gemeinsame Verteilung nicht explizit bekannt ist oder es schwierig ist, eine direkte Stichprobe zu ziehen, aber die bedingte Verteilung der einzelnen Variablen bekannt ist und es einfacher ist, eine Stichprobe zu ziehen.

Wir beginnen mit der Auswahl eines Anfangswerts für die Zufallsvariablen X & Y. Dann ziehen wir eine Stichprobe aus der bedingten Wahrscheinlichkeitsverteilung von X bei Y = Y⁰, bezeichnet als p(X|Y⁰). Im nächsten Schritt ziehen wir einen neuen Wert von Y unter der Bedingung von X¹, den wir gerade berechnet haben. Wir wiederholen das Verfahren für weitere n – 1 Iterationen, wobei wir abwechselnd eine neue Stichprobe aus der bedingten Wahrscheinlichkeitsverteilung von X und der bedingten Wahrscheinlichkeitsverteilung von Y ziehen, wenn der aktuelle Wert der anderen Zufallsvariablen gegeben ist.

Sehen wir uns ein Beispiel an. Angenommen, wir hätten die folgenden posterioren und bedingten Wahrscheinlichkeitsverteilungen.

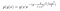
wobei g(y) die Terme enthält, die x nicht enthalten, und g(x) die Terme enthält, die nicht von y abhängen.

Wir kennen den Wert von C (Normalisierungskonstante) nicht. Wir kennen jedoch die bedingten Wahrscheinlichkeitsverteilungen. Daher können wir Gibbs Sampling verwenden, um die posteriore Verteilung zu approximieren.

Anmerkung: Die bedingten Wahrscheinlichkeiten sind in der Tat Normalverteilungen und können wie folgt umgeschrieben werden.

Aufgrund der vorangegangenen Gleichungen fahren wir fort, den Gibbs Sampling Algorithmus in Python umzusetzen. Zu Beginn importieren wir die folgenden Bibliotheken.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Wir definieren die Funktion für die Posterior-Verteilung (nehmen C=1 an).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Dann stellen wir die Wahrscheinlichkeitsverteilung dar.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Nun versuchen wir, die Wahrscheinlichkeitsverteilung mit Gibbs Sampling zu schätzen. Wie wir bereits erwähnt haben, sind die bedingten Wahrscheinlichkeiten Normalverteilungen. Daher können wir sie in Form von mu und sigma ausdrücken.

Im folgenden Codeblock definieren wir Funktionen für mu und sigma, initialisieren unsere Zufallsvariablen X & Y und setzen N (die Anzahl der Iterationen).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Wir durchlaufen den Gibbs-Sampling-Algorithmus.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Abschließend stellen wir die Ergebnisse dar.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Wie wir sehen können, die mit dem Gibbs-Sampling-Algorithmus erhaltene Wahrscheinlichkeitsverteilung eine gute Annäherung an die Zielverteilung darstellt.

Schlussfolgerung

Das Gibbs Sampling ist eine Monte-Carlo-Markov-Ketten-Methode, die iterativ eine Instanz aus der Verteilung jeder Variablen zieht, die von den aktuellen Werten der anderen Variablen abhängt, um komplexe gemeinsame Verteilungen zu schätzen. Im Gegensatz zum Metropolis-Hastings-Algorithmus akzeptieren wir immer den Vorschlag. Daher kann Gibbs Sampling viel effizienter sein.