Friedman-Test in SPSS Statistics
SPSS Statistics
SPSS Statistics Ausgabe für den Friedman-Test
SPSS Statistics erzeugt entweder zwei oder drei Tabellen, je nachdem, ob Sie zusätzlich zur Durchführung des Friedman-Tests die Erstellung von deskriptiven Statistiken und/oder Quartilen ausgewählt haben.
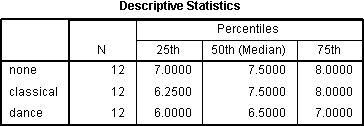
Tabelle der deskriptiven Statistik
Die Tabelle der deskriptiven Statistik wird erstellt, wenn Sie die Option Quartile ausgewählt haben:
Veröffentlicht mit schriftlicher Genehmigung von SPSS Statistics, IBM Corporation.
Dies ist eine sehr nützliche Tabelle, da sie verwendet werden kann, um in Ihrem Ergebnisabschnitt deskriptive Statistiken für jeden der Zeitpunkte oder Bedingungen (je nach Ihrem Studiendesign) für Ihre abhängige Variable zu präsentieren. Diese Nützlichkeit wird später im Abschnitt „Reporting the Output“ vorgestellt.
Rangtabelle
Die Rangtabelle zeigt den mittleren Rang für jede der verbundenen Gruppen, wie unten dargestellt:

Veröffentlicht mit schriftlicher Genehmigung von SPSS Statistics, IBM Corporation.
Der Friedman-Test vergleicht die mittleren Ränge zwischen den verbundenen Gruppen und zeigt an, wie sich die Gruppen unterscheiden. Es ist jedoch unwahrscheinlich, dass Sie diese Werte in Ihrem Ergebnisteil angeben, sondern Sie werden höchstwahrscheinlich den Medianwert für jede verwandte Gruppe angeben.
Teststatistiktabelle
Die Teststatistiktabelle informiert Sie über das tatsächliche Ergebnis des Friedman-Tests und darüber, ob ein statistisch signifikanter Unterschied zwischen den mittleren Rängen Ihrer verwandten Gruppen besteht. Für das in diesem Leitfaden verwendete Beispiel sieht die Tabelle wie folgt aus:

Veröffentlicht mit schriftlicher Genehmigung von SPSS Statistics, IBM Corporation.
Die obige Tabelle enthält den Wert der Teststatistik (χ2) („Chi-Quadrat“), die Freiheitsgrade („df“) und das Signifikanzniveau („Asymp. Sig.“), was alles ist, was wir brauchen, um das Ergebnis des Friedman-Tests zu melden. Anhand unseres Beispiels können wir sehen, dass es insgesamt einen statistisch signifikanten Unterschied zwischen den mittleren Rängen der entsprechenden Gruppen gibt. Es ist wichtig zu beachten, dass der Friedman-Test ein Omnibus-Test ist, wie seine parametrische Alternative, d. h. er sagt Ihnen, ob es allgemeine Unterschiede gibt, aber er zeigt nicht genau auf, welche Gruppen sich im Einzelnen voneinander unterscheiden. Dazu müssen Sie Post-Hoc-Tests durchführen, die nach dem nächsten Abschnitt besprochen werden.
SPSS-Statistik
Ausgabe des Friedman-Tests (ohne Post-Hoc-Tests)
Sie können das Ergebnis des Friedman-Tests wie folgt ausgeben:
- Allgemein
Es gab einen statistisch signifikanten Unterschied in der wahrgenommenen Anstrengung in Abhängigkeit davon, welche Art von Musik beim Laufen gehört wurde, χ2(2) = 7.600, p = 0,022.
Sie könnten auch die Medianwerte für jede der entsprechenden Gruppen angeben. In diesem Stadium wissen Sie jedoch nur, dass es irgendwo Unterschiede zwischen den verwandten Gruppen gibt, aber Sie wissen nicht genau, wo diese Unterschiede liegen. Denken Sie jedoch daran, dass Sie keine Post-Hoc-Tests durchführen sollten, wenn das Ergebnis des Friedman-Tests statistisch nicht signifikant ist.
Post-Hoc-Tests
Um zu untersuchen, wo die Unterschiede tatsächlich auftreten, müssen Sie separate Wilcoxon Signed-Rank-Tests für die verschiedenen Kombinationen der verwandten Gruppen durchführen. In diesem Beispiel würden Sie also die folgenden Kombinationen vergleichen:
- Keine zu Klassik.
- Keine zu Tanz.
- Klassik zu Tanz.
Sie müssen eine Bonferroni-Anpassung auf die Ergebnisse der Wilcoxon-Tests anwenden, da Sie mehrere Vergleiche durchführen, was die Wahrscheinlichkeit erhöht, dass Sie ein Ergebnis für signifikant erklären, obwohl dies nicht der Fall ist (Fehler vom Typ I). Zum Glück ist die Bonferroni-Anpassung sehr einfach zu berechnen: Nehmen Sie einfach das Signifikanzniveau, das Sie ursprünglich verwendet haben (in diesem Fall 0,05), und teilen Sie es durch die Anzahl der von Ihnen durchgeführten Tests. In diesem Beispiel haben wir also ein neues Signifikanzniveau von 0,05/3 = 0,017. Das bedeutet, wenn der p-Wert größer als 0,017 ist, liegt kein statistisch signifikantes Ergebnis vor.
Wenn Sie diese Tests (siehe Anleitung zum Wilcoxon-Signed-Rank-Test) auf die Ergebnisse dieses Beispiels anwenden, erhalten Sie folgendes Ergebnis:

Published with written permission from SPSS Statistics, IBM Corporation.
Diese Tabelle zeigt die Ergebnisse des Wilcoxon-Signed-Rank-Tests für jede unserer Kombinationen. Es ist wichtig zu beachten, dass die Signifikanzwerte in SPSS Statistics nicht angepasst wurden, um Mehrfachvergleiche zu kompensieren – Sie müssen die von SPSS Statistics erzeugten Signifikanzwerte manuell mit dem von Ihnen berechneten Bonferroni-bereinigten Signifikanzniveau vergleichen. Wir können sehen, dass auf dem Signifikanzniveau p < 0,017 nur die wahrgenommene Anstrengung zwischen keiner Musik und Tanzen (Tanzen-ohne, p = 0,008) statistisch signifikant unterschiedlich war.
SPSS-Statistik
Berichten Sie die Ergebnisse des Friedman-Tests (mit Post-Hoc-Tests)
Sie können die Ergebnisse des Friedman-Tests mit Post-Hoc-Tests wie folgt berichten:
- Allgemein
Es gab einen statistisch signifikanten Unterschied in der wahrgenommenen Anstrengung, je nachdem, welche Art von Musik beim Laufen gehört wurde, χ2(2) = 7.600, p = 0.022. Die Post-hoc-Analyse mit Wilcoxon Signed-Rank-Tests wurde mit einer Bonferroni-Korrektur durchgeführt, was zu einem Signifikanzniveau von p < 0,017 führte. Der Median (IQR) der wahrgenommenen Anstrengung für die Laufversuche ohne Musik, mit klassischer und mit Tanzmusik betrug 7,5 (7 bis 8), 7,5 (6,25 bis 8) bzw. 6,5 (6 bis 7). Es gab keine signifikanten Unterschiede zwischen dem Lauftest ohne Musik und dem Lauftest mit klassischer Musik (Z = -0,061, p = 0,952) oder zwischen dem Lauftest mit klassischer und dem Lauftest mit Tanzmusik (Z = -1,811, p = 0,070), obwohl die wahrgenommene Anstrengung beim Lauftest mit Tanzmusik im Vergleich zum Lauftest mit klassischer Musik insgesamt geringer war. Allerdings gab es eine statistisch signifikante Verringerung der wahrgenommenen Anstrengung in der Studie mit Tanzmusik im Vergleich zu keiner Musik (Z = -2,636, p = 0,008).
Leave a Reply