Une introduction douce au problème de la coque convexe

Les coques convexes ont tendance à être utiles dans de nombreux domaines différents, parfois de manière assez inattendue. Dans cet article, je vais expliquer l’Idée de base des coques convexes 2d et comment utiliser le scan de graham pour les trouver. Donc, si vous connaissez déjà le graham scan, alors cet article n’est pas pour vous, mais sinon, cela devrait vous familiariser avec certains des concepts pertinents.

La coque convexe d’un ensemble de points est définie comme le plus petit polygone convexe, qui entoure tous les points de l’ensemble. Convexe signifie que le polygone n’a aucun coin courbé vers l’intérieur.

Les bords rouges sur le polygone de droite entourent le coin où la forme est concave, l’opposé de convexe.

Une façon utile de penser à la coque convexe est l’analogie de l’élastique. Supposons que les points de l’ensemble soient des clous, dépassant d’une surface plane. Imaginez maintenant, ce qui se passerait si vous preniez un élastique et l’étiriez autour des clous. En essayant de se contracter pour retrouver sa longueur initiale, l’élastique enfermerait les clous, en touchant ceux qui dépassent le plus du centre.

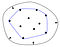
Pour représenter la coque convexe résultante en code, nous stockons habituellement la liste des points qui soutiennent cet élastique, c’est-à-dire la liste des points sur la coque convexe.

Notez que nous devons encore définir ce qui doit se passer si trois points se trouvent sur la même ligne. Si on imagine que l’élastique a un point où il touche l’un des clous mais qu’il ne s’y plie pas du tout, cela signifie que le clou qui s’y trouve se trouve sur une droite entre deux autres clous. Selon le problème, on peut considérer que ce clou situé le long de la ligne droite fait partie de la sortie, puisqu’il touche l’élastique. D’un autre côté, nous pourrions également dire que ce clou ne devrait pas faire partie de la sortie, car la forme de l’élastique ne change pas lorsque nous le retirons. Cette décision dépend du problème sur lequel vous travaillez actuellement, et mieux encore, si vous avez une entrée où aucun des trois points n’est colinéaire (c’est souvent le cas dans les tâches faciles pour les concours de programmation), alors vous pouvez même ignorer complètement ce problème.

Finir la coque convexe

En regardant un ensemble de points, l’intuition humaine nous permet de déterminer rapidement quels points sont susceptibles de toucher la coque convexe, et lesquels seront plus proches du centre et donc éloignés de la coque convexe. Mais traduire cette intuition en code demande un peu de travail.

Pour trouver la coque convexe d’un ensemble de points, nous pouvons utiliser un algorithme appelé le Scan de Graham, qui est considéré comme l’un des premiers algorithmes de géométrie computationnelle. En utilisant cet algorithme, nous pouvons trouver le sous-ensemble de points qui se trouvent sur la coque convexe, ainsi que l’ordre dans lequel ces points sont rencontrés en faisant le tour de la coque convexe.

L’algorithme commence par trouver un point, dont on sait qu’il se trouve sur la coque convexe avec certitude. Le point avec la coordonnée y la plus basse par exemple peut être considéré comme un choix sûr. Si plusieurs points existent à la même coordonnée y, on prend celui qui a la plus grande coordonnée x (cela fonctionne aussi avec d’autres points d’angle, par exemple d’abord le plus petit x puis le plus petit y).

Puis, nous trions les autres points par l’angle auquel ils se trouvent vus du point de départ. Si deux points se trouvent être au même angle, le point qui est plus proche du point de départ devrait apparaître plus tôt dans le tri.

Maintenant, l’idée de l’algorithme est de se promener autour de ce tableau trié, en déterminant pour chaque point, s’il se trouve ou non sur la coque convexe. Cela signifie que pour chaque triplet de points que nous rencontrons, nous décidons s’ils forment un coin convexe ou concave. Si le coin est concave, alors nous savons, que le point central hors de ce triplet ne peut pas se trouver sur la coque convexe.

(Notez que les termes coin concave et coin convexe doivent être utilisés par rapport à l’ensemble du polygone, juste un coin en soi ne peut pas être convexe ou concave, car il n’y aurait pas de direction de référence.)

Nous stockons les points qui se trouvent sur la coque convexe sur une pile, de cette façon nous pouvons ajouter des points si nous les atteignons sur notre chemin autour des points triés, et les enlever si nous découvrons qu’ils forment un coin concave.

(Strictement parlant, nous devons accéder aux deux points supérieurs de la pile, donc nous utilisons un std::vector à la place, mais nous pensons que c’est une sorte de pile, car nous ne sommes toujours concernés que par le couple d’éléments supérieurs.)

En faisant le tour du tableau trié de points, nous ajoutons le point à la pile, et si nous trouvons plus tard que le point n’appartient pas à la coque convexe, nous le supprimons.

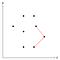
Nous pouvons mesurer si le coin actuel penche vers l’intérieur ou l’extérieur en calculant le produit en croix et en vérifiant si celui-ci est positif ou négatif. La figure ci-dessus montre un triplet de points où le coin qu’ils forment est convexe, donc celui du milieu parmi ces trois points reste sur la pile pour le moment.

Pour passer au point suivant, on continue à faire la même chose : vérifier si le coin est convexe et si non, enlever le point. Puis continuer à ajouter le point suivant et répéter.

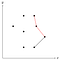
Ce coin marqué en rouge est concave, donc on enlève le point du milieu de la pile car il ne peut pas faire partie de la coque convexe.

Comment savons-nous que cela nous donnera la bonne réponse ?

Écrire une preuve rigoureuse est hors de portée de cet article, mais je peux écrire les idées de base. Je vous encourage cependant à continuer et à essayer de combler les lacunes !

Puisque nous avons calculé le produit en croix à chaque coin, nous savons avec certitude que nous obtenons un polygone convexe. Il ne nous reste plus qu’à prouver, que ce polygone convexe englobe vraiment tous les points.

(En fait, il faudrait aussi montrer que c’est le plus petit polygone convexe possible satisfaisant à ces conditions, mais cela découle assez facilement du fait que les points d’angle de notre polygone convexe sont un sous-ensemble de l’ensemble initial de points.)

Supposons qu’il existe un point P en dehors du polygone que nous venons de trouver.

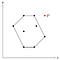
Puisque chaque point a été ajouté à la pile une fois, nous savons que P a été retiré de la pile à un moment donné. Cela signifie, que P, avec ses points voisins, appelons-les O et Q, a formé un coin concave.

Puisque O et Q se trouvent à l’intérieur du polygone (ou sur sa frontière), P devrait se trouver également à l’intérieur de la frontière, car le polygone est convexe et le coin que O et Q forment avec P est concave par rapport au polygone.

Nous avons donc trouvé une contradiction, ce qui signifie qu’un tel point P ne peut pas exister.

Implémentation

L’implémentation ici fournie a une fonction convex_hull, qui prend un std::vectorqui contient les points comme std::pairs d’ints et renvoie un autre std::vectorqui contient les points qui se trouvent sur la coque convexe.

Analyse du temps d’exécution et de la mémoire

Il est toujours utile de penser aux algorithmes de complexité en termes de notation Big-O, que je n’expliquerai pas ici, car Michael Olorunnisola ici présent a déjà fait un bien meilleur travail d’explication que je ne le ferais probablement :

Trier les points prend initialement O(n log n) temps, mais après cela, chaque étape peut être calculée en temps constant. Chaque point est ajouté et retiré de la pile au plus une fois, ce qui signifie que le temps d’exécution dans le pire des cas se situe dans O(n log n).

L’utilisation de la mémoire, qui se situe dans O(n) pour le moment, pourrait être optimisée en supprimant le besoin de la pile et en effectuant les opérations directement sur le tableau d’entrée. Nous pourrions déplacer les points qui se trouvent sur la coque convexe au début du tableau d’entrée et les arranger dans le bon ordre, et les autres points seraient déplacés vers le reste du tableau. La fonction pourrait alors retourner une seule variable entière indiquant le nombre de points du tableau qui se trouvent sur la coque convexe. Cela a bien sûr l’inconvénient de rendre la fonction beaucoup plus compliquée, je vous le déconseille donc, à moins que vous ne codiez pour des systèmes embarqués ou que vous ayez des problèmes de mémoire aussi restrictifs. Pour la plupart des situations, le compromis probabilité de bogue/économie de mémoire n’en vaut tout simplement pas la peine.

Autres algorithmes

Une alternative au Graham Scan est l’algorithme de Chan, qui est basé sur effectivement la même idée mais est plus facile à mettre en œuvre. Il est judicieux de comprendre d’abord comment fonctionne le Graham Scan cependant.

Si vous vous sentez vraiment fantaisiste et que vous voulez aborder le problème en trois dimensions, jetez un coup d’œil à l’algorithme de Preparata et Hong introduit dans leur article de 1977 « Convex Hulls of Finite Sets of Points in Two and Three Dimensions ».