Une brève introduction à la confidentialité différentielle
.
Aaruran Elamurugaiyan
La vie privée peut être quantifiée. Mieux encore, nous pouvons classer les stratégies de préservation de la vie privée et dire laquelle est la plus efficace. Mieux encore, nous pouvons concevoir des stratégies qui sont robustes même contre les hackers qui disposent d’informations auxiliaires. Et comme si cela ne suffisait pas, nous pouvons faire toutes ces choses simultanément. Ces solutions, et plus encore, résident dans une théorie probabiliste appelée la confidentialité différentielle.
Voici le contexte. Nous conservons (ou gérons) une base de données sensible et nous aimerions diffuser certaines statistiques de ces données au public. Cependant, nous devons nous assurer qu’il est impossible pour un adversaire d’effectuer une rétro-ingénierie des données sensibles à partir de ce que nous avons publié . Dans ce cas, un adversaire est une partie qui a l’intention de révéler, ou d’apprendre, au moins certaines de nos données sensibles. La confidentialité différentielle peut résoudre les problèmes qui se posent lorsque ces trois ingrédients – données sensibles, conservateurs qui doivent publier des statistiques et adversaires qui veulent récupérer les données sensibles – sont présents (voir figure 1). Cette rétro-ingénierie est un type de violation de la vie privée.

Mais à quel point est-il difficile de violer la vie privée ? L’anonymisation des données ne serait-elle pas suffisante ? Si vous avez des informations auxiliaires provenant d’autres sources de données, l’anonymisation ne suffit pas. Par exemple, en 2007, Netflix a publié un ensemble de données sur les évaluations de ses utilisateurs dans le cadre d’un concours visant à déterminer si quelqu’un pouvait surpasser son algorithme de filtrage collaboratif. L’ensemble de données ne contenait pas d’informations d’identification personnelle, mais les chercheurs ont quand même réussi à violer la vie privée ; ils ont récupéré 99 % de toutes les informations personnelles qui avaient été supprimées de l’ensemble de données. Dans ce cas, les chercheurs ont violé la vie privée en utilisant des informations auxiliaires provenant d’IMDB.
Comment peut-on se défendre contre un adversaire qui dispose d’une aide inconnue, et peut-être illimitée, du monde extérieur ? La confidentialité différentielle offre une solution. Les algorithmes à confidentialité différentielle sont résilients aux attaques adaptatives qui utilisent des informations auxiliaires . Ces algorithmes s’appuient sur l’incorporation de bruit aléatoire dans le mélange, de sorte que tout ce qu’un adversaire reçoit devient bruyant et imprécis, et qu’il est donc beaucoup plus difficile de violer la confidentialité (si c’est faisable du tout).
Comptage bruyant
Regardons un exemple simple d’injection de bruit. Supposons que nous gérons une base de données de cotes de crédit (résumée par le tableau 1).
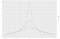
Pour cet exemple, supposons que l’adversaire veut connaître le nombre de personnes qui ont une mauvaise cote de crédit (qui est de 3). Les données sont sensibles, nous ne pouvons donc pas révéler la vérité de base. À la place, nous utiliserons un algorithme qui renvoie la vérité de base, N = 3, plus un certain bruit aléatoire. Cette idée de base (ajouter un bruit aléatoire à la vérité de base) est la clé de la confidentialité différentielle. Disons que nous choisissons un nombre aléatoire L dans une distribution de Laplace centrée sur zéro avec un écart type de 2. Nous retournons N+L. Nous allons expliquer le choix de l’écart-type dans quelques paragraphes. (Si vous n’avez jamais entendu parler de la distribution de Laplace, consultez la figure 2). Nous appellerons cet algorithme « comptage bruyant ».
Si nous allons déclarer une réponse absurde et bruyante, quel est l’intérêt de cet algorithme ? La réponse est qu’il nous permet de trouver un équilibre entre utilité et confidentialité. Nous voulons que le grand public tire une certaine utilité de notre base de données, sans exposer de données sensibles à un éventuel adversaire.
Que recevrait réellement l’adversaire ? Les réponses sont rapportées dans le tableau 2.

La première réponse que l’adversaire reçoit est proche, mais pas égale, à la vérité terrain. En ce sens, l’adversaire est trompé, l’utilité est fournie et la vie privée est protégée. Mais après plusieurs tentatives, il sera en mesure d’estimer la vérité de base. Cette « estimation à partir de requêtes répétées » est l’une des limites fondamentales de la confidentialité différentielle. Si l’adversaire peut effectuer suffisamment de requêtes dans une base de données à confidentialité différentielle, il peut toujours estimer les données sensibles. En d’autres termes, avec de plus en plus de requêtes, la confidentialité est violée. Le tableau 2 démontre empiriquement cette violation de la confidentialité. Cependant, comme vous pouvez le voir, l’intervalle de confiance à 90 % de ces 5 requêtes est assez large ; l’estimation n’est pas encore très précise.
Quelle peut être la précision de cette estimation ? Jetez un coup d’œil à la figure 3 où nous avons effectué une simulation plusieurs fois et tracé les résultats .

Chaque ligne verticale illustre la largeur d’un intervalle de confiance de 95%, et les points indiquent la moyenne des données échantillonnées de l’adversaire. Notez que ces graphiques ont un axe horizontal logarithmique et que le bruit est tiré de variables aléatoires de Laplace indépendantes et identiquement distribuées. Globalement, la moyenne est plus bruyante avec moins de requêtes (puisque les tailles d’échantillon sont petites). Comme prévu, les intervalles de confiance deviennent plus étroits à mesure que l’adversaire effectue plus de requêtes (puisque la taille de l’échantillon augmente et que le bruit tend vers zéro). Juste en inspectant le graphique, nous pouvons voir qu’il faut environ 50 requêtes pour faire une estimation décente.
Réfléchissons à cet exemple. Tout d’abord, en ajoutant du bruit aléatoire, nous avons rendu plus difficile pour un adversaire de violer la vie privée. Deuxièmement, la stratégie de dissimulation que nous avons employée était simple à mettre en œuvre et à comprendre. Malheureusement, avec de plus en plus de requêtes, l’adversaire était capable d’approcher le vrai compte.
Si nous augmentons la variance du bruit ajouté, nous pouvons mieux défendre nos données, mais nous ne pouvons pas simplement ajouter n’importe quel bruit de Laplace à une fonction que nous voulons dissimuler. La raison en est que la quantité de bruit que nous devons ajouter dépend de la sensibilité de la fonction, et chaque fonction a sa propre sensibilité. En particulier, la fonction de comptage a une sensibilité de 1. Voyons ce que signifie la sensibilité dans ce contexte.
Sensibilité et mécanisme de Laplace
Pour une fonction:
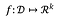
la sensibilité de f est :
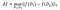
sur des ensembles de données D₁, D₂ différant sur au plus un élément .
La définition ci-dessus est assez mathématique, mais elle n’est pas aussi mauvaise qu’il n’y paraît. Grosso modo, la sensibilité d’une fonction est la plus grande différence possible qu’une ligne peut avoir sur le résultat de cette fonction, pour n’importe quel ensemble de données. Par exemple, dans notre jeu de données jouet, le comptage du nombre de lignes a une sensibilité de 1, parce que l’ajout ou la suppression d’une seule ligne de n’importe quel jeu de données modifiera le comptage d’au plus 1.
Au titre d’autre exemple, supposons que nous pensions à « compter arrondi à un multiple de 5 ». Cette fonction a une sensibilité de 5, et nous pouvons le montrer assez facilement. Si nous avons deux ensembles de données de taille 10 et 11, ils diffèrent sur une ligne, mais les « comptes arrondis à un multiple de 5 » sont respectivement de 10 et 15. En fait, cinq est la plus grande différence possible que cet exemple de fonction peut produire. Par conséquent, sa sensibilité est de 5.
Calculer la sensibilité d’une fonction arbitraire est difficile. Une quantité considérable d’efforts de recherche est consacrée à l’estimation des sensibilités , à l’amélioration des estimations de la sensibilité , et au contournement du calcul de la sensibilité .
Comment la sensibilité se rapporte-t-elle au comptage bruyant ? Notre stratégie de comptage bruyant a utilisé un algorithme appelé le mécanisme de Laplace , qui à son tour repose sur la sensibilité de la fonction qu’il obscurcit . Dans l’algorithme 1, nous avons une implémentation pseudocode naïve du mécanisme de Laplace .
Algorithme 1
Entrée : Fonction F, Entrée X, Niveau de confidentialité ϵ
Sortie : Une réponse bruyante
Calculer F (X)
Calculer la sensibilité de de F : S
Tirer le bruit L d’une distribution de Laplace avec une variance :
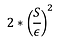
Retourner F(X) + L
Plus la sensibilité S est grande, plus la réponse sera bruyante. Le comptage a seulement une sensibilité de 1, donc nous n’avons pas besoin d’ajouter beaucoup de bruit pour préserver la vie privée.
Notez que le mécanisme de Laplace dans l’algorithme 1 consomme un paramètre epsilon. Nous appellerons cette quantité la perte de confidentialité du mécanisme et elle fait partie de la définition la plus centrale dans le domaine de la confidentialité différentielle : la confidentialité différentielle epsilon. Pour illustrer, si nous rappelons notre exemple précédent et utilisons un peu d’algèbre, nous pouvons voir que notre mécanisme de comptage bruyant a une confidentialité différentielle epsilon, avec un epsilon de 0,707. En réglant epsilon, nous contrôlons le caractère bruyant de notre comptage bruyant. Le choix d’un epsilon plus petit produit des résultats plus bruyants et de meilleures garanties de confidentialité. À titre de référence, Apple utilise un epsilon de 2 dans l’autocorrection différentielle de son clavier .
La quantité epsilon est la façon dont la confidentialité différentielle peut fournir des comparaisons rigoureuses entre différentes stratégies. La définition formelle de la confidentialité différentielle epsilon est un peu plus impliquée mathématiquement, donc je l’ai intentionnellement omise de ce billet de blog. Vous pouvez en lire plus à ce sujet dans l’étude de Dwork sur la confidentialité différentielle.
Comme vous vous en souvenez, l’exemple du comptage bruyant avait un epsilon de 0,707, ce qui est assez petit. Mais nous avons quand même violé la confidentialité après 50 requêtes. Pourquoi ? Parce qu’avec l’augmentation des requêtes, le budget de confidentialité augmente, et donc la garantie de confidentialité est pire.
Le budget de confidentialité
En général, les pertes de confidentialité s’accumulent. Lorsque deux réponses sont renvoyées à un adversaire, la perte totale de confidentialité est deux fois plus importante, et la garantie de confidentialité est deux fois moins forte. Cette propriété cumulative est une conséquence du théorème de composition. En substance, à chaque nouvelle requête, des informations supplémentaires sur les données sensibles sont divulguées. Par conséquent, le théorème de composition a une vision pessimiste et suppose le pire des scénarios : la même quantité de fuites se produit avec chaque nouvelle réponse. Pour de fortes garanties de confidentialité, nous voulons que la perte de confidentialité soit faible. Ainsi, dans notre exemple où nous avons une perte de confidentialité de trente-cinq (après 50 requêtes à notre mécanisme de comptage bruyant de Laplace), la garantie de confidentialité correspondante est fragile.
Comment la confidentialité différentielle fonctionne-t-elle si la perte de confidentialité augmente si rapidement ? Pour assurer une garantie de confidentialité significative, les conservateurs de données peuvent appliquer une perte de confidentialité maximale. Si le nombre de requêtes dépasse ce seuil, la garantie de confidentialité devient trop faible et le conservateur cesse de répondre aux requêtes. La perte maximale de confidentialité est appelée le budget de confidentialité . Nous pouvons considérer chaque requête comme une « dépense » de confidentialité qui entraîne une perte de confidentialité progressive. La stratégie d’utilisation des budgets, des dépenses et des pertes est connue de manière appropriée sous le nom de comptabilité de la vie privée .
La comptabilité de la vie privée est une stratégie efficace pour calculer la perte de vie privée après plusieurs requêtes, mais elle peut encore intégrer le théorème de composition. Comme indiqué précédemment, le théorème de composition suppose le pire scénario. En d’autres termes, de meilleures alternatives existent.
Deep Learning
L’apprentissage profond est un sous-domaine de l’apprentissage automatique, qui se rapporte à la formation de réseaux neuronaux profonds (DNN) pour estimer des fonctions inconnues . (À un haut niveau, un DNN est une séquence de transformations affines et non linéaires mettant en correspondance un espace à n dimensions avec un espace à m dimensions). Ses applications sont très répandues et il n’est pas nécessaire de les rappeler ici. Nous allons explorer comment former un réseau de neurones profonds en privé.
Les réseaux de neurones profonds sont généralement formés en utilisant une variante de la descente de gradient stochastique (SGD). Abadi et al. ont inventé une version préservant la vie privée de cet algorithme populaire, communément appelée » SGD privée » (ou PSGD). La figure 4 illustre la puissance de leur nouvelle technique. Abadi et al. ont inventé une nouvelle approche : le comptable des moments. L’idée de base derrière le comptable de moments est d’accumuler les dépenses de confidentialité en encadrant la perte de confidentialité comme une variable aléatoire, et en utilisant ses fonctions génératrices de moments pour mieux comprendre la distribution de cette variable (d’où le nom) . Les détails techniques complets sont en dehors de la portée d’un billet de blog d’introduction, mais nous vous encourageons à lire le papier original pour en savoir plus.

Pensées finales
Nous avons examiné la théorie de la confidentialité différentielle et vu comment elle peut être utilisée pour quantifier la confidentialité. Les exemples de ce post montrent comment les idées fondamentales peuvent être appliquées et le lien entre l’application et la théorie. Il est important de se rappeler que les garanties de confidentialité se détériorent avec l’utilisation répétée, il est donc utile de réfléchir à la façon d’atténuer ce phénomène, que ce soit avec la budgétisation de la confidentialité ou d’autres stratégies. Vous pouvez étudier cette détérioration en cliquant sur cette phrase et en répétant nos expériences. Il reste de nombreuses questions auxquelles nous n’avons pas répondu ici et une abondante littérature à explorer – voir les références ci-dessous. Nous vous encourageons à lire davantage.
Cynthia Dwork. Confidentialité différentielle : Une enquête sur les résultats. Conférence internationale sur la théorie et les applications des modèles de calcul, 2008.
Contributeurs de Wikipédia. Distribution de Laplace, juillet 2018.
Aaruran Elamurugaiyan. Graphiques démontrant l’erreur standard des réponses différentiellement privées sur le nombre de requêtes, août 2018.
Benjamin I. P. Rubinstein et Francesco Alda. La confidentialité différentielle aléatoire sans douleur avec l’échantillonnage de sensibilité. In 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork et Aaron Roth. Les fondements algorithmiques de la confidentialité différentielle . Now Publ, 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar, et Li Zhang. Apprentissage profond avec confidentialité différentielle. Actes de la conférence 2016 de l’ACM SIGSAC sur la sécurité des ordinateurs et des communications – CCS16 , 2016.
Frank D. McSherry. Requêtes intégrées à la confidentialité : Une plate-forme extensible pour l’analyse de données préservant la vie privée. Dans les actes de la conférence internationale ACM SIGMOD 2009 sur la gestion des données , SIGMOD ’09, pages 19-30, New York, NY, États-Unis, 2009. ACM.
Contributeurs de Wikipédia. Deep Learning, août 2018.
Leave a Reply