Test de Friedman dans SPSS Statistics

SPSS Statistics

Sortie de SPSS Statistics pour le test de Friedman

SPSS Statistics génère deux ou trois tableaux, selon que vous avez choisi de faire générer des descriptifs et/ou des quartiles en plus de l’exécution du test de Friedman.

Tableau des statistiques descriptives

Le tableau des statistiques descriptives sera produit si vous avez sélectionné l’option Quartiles :

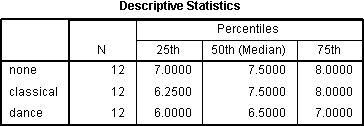
Publié avec l’autorisation écrite de SPSS Statistics, IBM Corporation.

Ce tableau est très utile car il peut être utilisé pour présenter des statistiques descriptives dans votre section de résultats pour chacun des points temporels ou des conditions (selon le plan de votre étude) pour votre variable dépendante. Cette utilité sera présentée dans la section « Présentation des résultats » plus loin.

Tableau des rangs

Le tableau des rangs montre le rang moyen pour chacun des groupes liés, comme indiqué ci-dessous :

Publié avec la permission écrite de SPSS Statistics, IBM Corporation.

Le test de Friedman compare les rangs moyens entre les groupes liés et indique comment les groupes diffèrent, et il est inclus pour cette raison. Cependant, il est peu probable que vous fassiez réellement état de ces valeurs dans votre section de résultats, mais il est plus probable que vous fassiez état de la valeur médiane pour chaque groupe apparenté.

Tableau des statistiques du test

Le tableau des statistiques du test vous informe du résultat réel du test de Friedman et vous indique s’il y avait une différence globale statistiquement significative entre les rangs moyens de vos groupes apparentés. Pour l’exemple utilisé dans ce guide, le tableau se présente comme suit :

Publié avec l’autorisation écrite de SPSS Statistics, IBM Corporation.

Le tableau ci-dessus fournit la valeur de la statistique de test (χ2) ( » Chi-square « ), les degrés de liberté ( » df « ) et le niveau de signification ( » Asymp. Sig. « ), ce qui est tout ce dont nous avons besoin pour rapporter le résultat du test de Friedman. Dans notre exemple, nous pouvons constater qu’il existe une différence globale statistiquement significative entre les rangs moyens des groupes apparentés. Il est important de noter que le test de Friedman est un test omnibus, comme son alternative paramétrique ; c’est-à-dire qu’il vous indique s’il existe des différences globales, mais ne précise pas quels groupes en particulier diffèrent les uns des autres. Pour cela, vous devez effectuer des tests post hoc, que nous aborderons après la section suivante.

Statistiques SPSS

Rapport du résultat du test de Friedman (sans tests post hoc)

Vous pouvez rapporter le résultat du test de Friedman comme suit :

Vous pourriez également inclure les valeurs médianes pour chacun des groupes apparentés. Cependant, à ce stade, vous savez seulement qu’il existe des différences quelque part entre les groupes apparentés, mais vous ne savez pas exactement où se situent ces différences. Rappelez-vous cependant que si le résultat de votre test de Friedman n’était pas statistiquement significatif, vous ne devez pas effectuer de tests post hoc.

Tests post hoc

Pour examiner où se situent réellement les différences, vous devez effectuer des tests séparés de Wilcoxon signed-rank sur les différentes combinaisons de groupes apparentés. Ainsi, dans cet exemple, vous comparerez les combinaisons suivantes :

• Aucune à Classique.
• Aucune à Danse.
• Classique à Danse.

Vous devez utiliser un ajustement de Bonferroni sur les résultats que vous obtenez à partir des tests de Wilcoxon parce que vous faites des comparaisons multiples, ce qui rend plus probable que vous déclariez un résultat significatif alors que vous ne devriez pas (une erreur de type I). Heureusement, l’ajustement de Bonferroni est très facile à calculer ; il suffit de prendre le niveau de signification que vous utilisiez initialement (dans ce cas, 0,05) et de le diviser par le nombre de tests que vous effectuez. Ainsi, dans cet exemple, nous avons un nouveau niveau de signification de 0,05/3 = 0,017. Cela signifie que si la valeur p est supérieure à 0,017, nous n’avons pas de résultat statistiquement significatif.

En exécutant ces tests (voir comment avec notre guide du test de Wilcoxon signed-rank) sur les résultats de cet exemple, vous obtenez le résultat suivant :

Publié avec l’autorisation écrite de SPSS Statistics, IBM Corporation.

Ce tableau montre la sortie du test de Wilcoxon signed-rank sur chacune de nos combinaisons. Il est important de noter que les valeurs de signification n’ont pas été ajustées dans SPSS Statistics pour compenser les comparaisons multiples – vous devez comparer manuellement les valeurs de signification produites par SPSS Statistics au niveau de signification ajusté par Bonferroni que vous avez calculé. Nous pouvons voir qu’au niveau de signification p < 0,017, seul l’effort perçu entre l’absence de musique et la danse (dance-none, p = 0,008) était statistiquement différent.

Statistiques SPSS

Rapport des résultats du test de Friedman (avec tests post hoc)

Vous pouvez rapporter les résultats du test de Friedman avec tests post hoc comme suit :