Recherche de grille pour le réglage du modèle

Un hyperparamètre de modèle est une caractéristique d’un modèle qui est externe au modèle et dont la valeur ne peut pas être estimée à partir des données. La valeur de l’hyperparamètre doit être définie avant le début du processus d’apprentissage. Par exemple, c dans les machines à vecteurs de support, k dans les k-voisins les plus proches, le nombre de couches cachées dans les réseaux neuronaux.

A l’inverse, un paramètre est une caractéristique interne du modèle et sa valeur peut être estimée à partir des données. Exemple, les coefficients bêta de la régression linéaire/logistique ou les vecteurs de support dans les Machines à Vecteur de Support.

La recherche en grille est utilisée pour trouver les hyperparamètres optimaux d’un modèle qui aboutit aux prédictions les plus  » précises « .

Examinons la recherche en grille en construisant un modèle de classification sur le jeu de données du cancer du sein.

Importez le jeu de données et visualisez les 10 premières lignes.

Sortie :

Chaque ligne du jeu de données a une des deux classes possibles : bénigne (représentée par 2) et maligne (représentée par 4). Aussi, il y a 10 attributs dans ce jeu de données (montré ci-dessus) qui seront utilisés pour la prédiction, sauf le numéro de code de l’échantillon qui est le numéro d’identification.

Nettoyons les données et renommons les valeurs de classe en 0/1 pour la construction du modèle (où 1 représente un cas malin). Observons également la distribution de la classe.

Sortie :

Il y a 444 cas bénins et 239 cas malins.

Sortie :

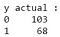
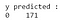
D’après la sortie, nous pouvons observer qu’il y a 68 cas malins et 103 cas bénins dans le jeu de données de test. Cependant, notre classificateur prédit que tous les cas sont bénins (car c’est la classe majoritaire).

Calculez les métriques d’évaluation de ce modèle.

Sortie :

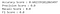
La précision du modèle est de 60.2%, mais il s’agit d’un cas où la précision n’est peut-être pas la meilleure métrique pour évaluer le modèle. Donc, regardons les autres métriques d’évaluation.

La figure ci-dessus est la matrice de confusion, avec des étiquettes et des couleurs ajoutées pour une meilleure intuition (le code pour générer ceci peut être trouvé ici). Pour résumer la matrice de confusion : VRAIS POSITIFS (TP)= 0,VRAIS NÉGATIFS (TN)= 103,FAUX POSITIFS (FP)= 0, FAUX NÉGATIFS (FN)= 68. Les formules des métriques d’évaluation sont les suivantes :

Puisque le modèle ne classe correctement aucun cas malin, les métriques de rappel et de précision sont égales à 0.

Maintenant que nous avons la précision de base, construisons un modèle de régression logistique avec les paramètres par défaut et évaluons le modèle.

Sortie :

En ajustant le modèle de régression logistique avec les paramètres par défaut, nous avons un bien « meilleur » modèle. L’exactitude est de 94,7 % et, dans le même temps, la précision est de 98,3 %. Maintenant, regardons à nouveau la matrice de confusion pour les résultats de ce modèle :

En regardant les instances mal classées, nous pouvons observer que 8 cas malins ont été classés incorrectement comme bénins (faux négatifs). De même, un seul cas bénin a été classé comme malin (Faux positifs).

Un faux négatif est plus grave car une maladie a été ignorée, ce qui peut conduire au décès du patient. Dans le même temps, un faux positif conduirait à un traitement inutile – entraînant un coût supplémentaire.

Tentons de minimiser les faux négatifs en utilisant la recherche par grille pour trouver les paramètres optimaux. La recherche par grille peut être utilisée pour améliorer toute métrique d’évaluation spécifique.

La métrique sur laquelle nous devons nous concentrer pour réduire les faux négatifs est le rappel.

Recherche par grille pour maximiser le Recall

Sortie :

Les hyperparamètres que nous avons accordés sont :

1. Pénalité : l1 ou l2 qui espèce la norme utilisée dans la pénalisation.
2. C : Inverse de la force de régularisation- des valeurs plus petites de C spécifient une régularisation plus forte.

De plus, dans la fonction Grid-search, nous avons le paramètre de scoring où nous pouvons spécifier la métrique pour évaluer le modèle sur (Nous avons choisi le rappel comme métrique). À partir de la matrice de confusion ci-dessous, nous pouvons voir que le nombre de faux négatifs a diminué, mais au prix d’une augmentation des faux positifs. Le rappel après la recherche sur grille a bondi de 88,2% à 91,1%, tandis que la précision a chuté de 98,3% à 87,3%.

Vous pouvez affiner le modèle pour trouver un équilibre entre la précision et le rappel en utilisant le score ‘f1’ comme métrique d’évaluation. Consultez cet article pour mieux comprendre les métriques d’évaluation.

La recherche en grille construit un modèle pour chaque combinaison d’hyperparamètres spécifiés et évalue chaque modèle. Une technique plus efficace pour le réglage des hyperparamètres est la recherche aléatoire – où des combinaisons aléatoires des hyperparamètres sont utilisées pour trouver la meilleure solution.