Résonance de Helmholtz
- Analyse de la résonance de Helmholtz
- Résonance, impédance, dépendance de phase et de fréquence
- Complications impliquant la longueur
- Résonances de Helmholtz et guitares
Analyse de la résonance de Helmholtz
Passons maintenant au quantitatif : Tout d’abord, nous allons supposer que la longueur d’onde du son produit est beaucoup plus longue que les dimensions du résonateur. Pour les bouteilles de l’animation en haut de cette page, les longueurs d’onde sont respectivement de 180 et 74 cm, donc cette approximation est assez bonne, mais il est utile de la vérifier chaque fois que vous commencez à décrire quelque chose comme un oscillateur de Helmholtz. La conséquence de cette approximation est que nous pouvons négliger les variations de pression à l’intérieur du volume du récipient : l’oscillation de pression aura la même phase partout à l’intérieur du récipient.
Soit l’air dans le goulot a une longueur effective L et une section transversale S. Sa masse est alors SL fois la densité de l’air ρ. (Certaines complications concernant la longueur effective sont discutées à la fin de cette page). Si ce « bouchon » d’air descend sur une petite distance x dans la bouteille, il comprime l’air dans le récipient de sorte que l’air qui occupait auparavant le volume V a maintenant un volume V – Sx. Par conséquent, la pression de cet air augmente de la pression atmosphérique PA à une valeur supérieure PA + p.
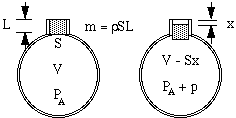
Maintenant, vous pourriez penser que l’augmentation de la pression serait juste proportionnelle à la diminution du volume. Ce serait le cas si la compression se produisait si lentement que la température ne changeait pas. Dans les vibrations qui donnent naissance au son, cependant, les changements sont rapides et donc la température augmente lors de la compression, ce qui donne un plus grand changement de pression. Techniquement, ils sont adiabatiques, ce qui signifie que la chaleur n’a pas le temps de se déplacer, et l’équation qui en résulte implique une constante γ, le rapport des chaleurs spécifiques, qui est d’environ 1,4 pour l’air. (Ceci est expliqué en annexe.) Par conséquent, la variation de pression p produite par un petit changement de volume ΔV est juste
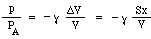
Maintenant, la masse m est déplacée par la différence de pression entre le haut et le bas du goulot, c’est-à-dire une force nette pS, donc nous écrivons la loi de Newton pour l’accélération a :
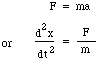
en substituant pour F et m donne : 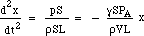
Donc la force de rappel est proportionnelle au déplacement. C’est la condition pour un mouvement harmonique simple, et il a une fréquence qui est 1/2π fois la racine carrée de la constante de proportionnalité, donc
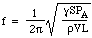
Maintenant la vitesse c du son dans l’air est déterminée par la densité, la pression et le rapport des chaleurs spécifiques, donc nous pouvons écrire :
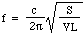
Mettons quelques chiffres : pour une bouteille d’un litre, avec S = 3 centimètres carrés et L = 5 centimètres, la fréquence est de 130 Hz, ce qui correspond à peu près au do inférieur au do moyen. (Voir notes.) La longueur d’onde est donc de 2,6 mètres, ce qui est beaucoup plus grand que la bouteille. Cela justifie, post hoc, l’hypothèse faite au début de la dérivation.
Résonance, impédance, dépendance de phase et de fréquence
Cette section peut être lue seule, mais si vous voulez un contexte plus détaillé, voir Oscillations, Oscillations forcées et Conformité acoustique, inertance et impédance.
Revenons à la représentation mécanique et regardons le résonateur de Helmholtz de l’extérieur, comme le montre le premier schéma : nous poussons avec une force oscillatoire F, de fréquence f ,la masse m (l’air dans le col du résonateur), qui s’appuie sur le ressort (l’air enfermé) de constante de rappel k, dont l’autre extrémité est fixe (l’air du résonateur ne peut pas s’échapper). De façon irréaliste, nous négligerons la gravité et la friction (pour l’instant).
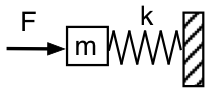
La force nécessaire pour accélérer la masse est proportionnelle à l’accélération et donc proportionnelle à f2. A une fréquence suffisamment basse, la force nécessaire pour accélérer la masse est négligeable, donc F n’a qu’à comprimer et étendre le ressort. Ainsi, dans cette limite, la force appliquée F = +kx. (La force du ressort est -kx.) L’impédance mécanique du système à cette basse fréquence est souple ou élastique. Acoustiquement, cela ressemble à une compliance acoustique : on pousse la masse d’air dans le manche et on comprime l’air dans le résonateur. La force appliquée F à droite est en phase avec x mesuré à droite, elle est donc à 90° derrière la vélocité et la pression appliquée est à 90° derrière le flux acoustique dans le résonateur.
Rappellez-vous que f2 dépend de l’accélération. Ainsi, à une fréquence suffisamment élevée, la force du ressort est négligeable par rapport à celle qui accélère la masse. F est donc en phase avec l’accélération, ce qui la place à 90° devant la vitesse. Sur le plan acoustique, la pression appliquée est en avance de 90° sur le flux acoustique dans le résonateur. Il s’agit d’une inertance mécanique ou acoustique.
À la fréquence de résonance (on parle toujours du croquis ci-dessus), l’amplitude peut être grande pour une très petite force. Donc à la résonance, l’impédance est très faible, vue de la force appliquée à la masse depuis l’extérieur (le schéma ci-dessus). A la résonance, le flux entrant et sortant du résonateur est maximal.
Envisageons maintenant ce qui se passe si nous regardons la pression à l’intérieur du résonateur (loin du col). Ici, nous regardons la force sur le ressort, donc notre analogue mécanique ressemble à ce schéma.
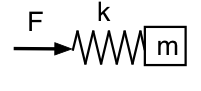
Cette fois, la basse fréquence signifie que la force peut être petite pour une amplitude donnée : le ressort et la masse se déplacent ensemble comme une masse, et le système semble cette fois inertiel à basse fréquence. À haute fréquence, la masse bouge à peine, et le système ressemble à un ressort ou est souple. Les relations de phase sont donc opposées à ce que nous avions auparavant : à basse f, p précède U de 90° ; à haute f, p retarde U de 90°.
Complications faisant intervenir la longueur effective
Le premier schéma de cette page dessine le « bouchon » d’air comme s’il s’agissait d’un cylindre qui se termine proprement à chaque extrémité du goulot de la bouteille. C’est une simplification excessive. En pratique, un volume supplémentaire, tant à l’intérieur qu’à l’extérieur, se déplace avec l’air dans le goulot – comme le suggère l’animation ci-dessus. La longueur supplémentaire qui devrait être ajoutée à la longueur géométrique du col est typiquement (et très approximativement) de 0,6 fois le rayon à l’extrémité extérieure, et un rayon à l’extrémité intérieure).
|
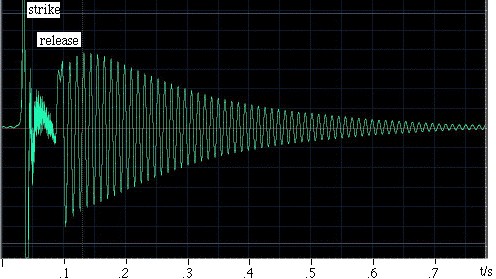
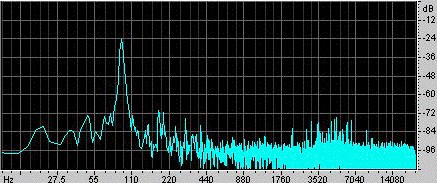
Un exemple. Ra Inta a fait cet exemple. Il prit un résonateur de Helmholtz sphérique d’un volume de 0,00292 m3 et un col cylindrique de longueur 0,080 m et de section 0,00083 m2. Pour l’exciter, il le frappe avec la paume de sa main, puis le relâche. Un microphone placé à l’intérieur du résonateur enregistre le son, qui est représenté dans l’oscillogramme de gauche. Vous pouvez voir que la main scelle le résonateur pendant plutôt moins de 0,1 s, et que pendant ce temps les oscillations sont plus faibles et de fréquence relativement élevée. Une fois la main relâchée, une oscillation s’établit, qui s’éteint progressivement en perdant de l’énergie par traînée visqueuse et turbulente, et aussi par rayonnement sonore. Un examen attentif montre que la fréquence augmente légèrement au fur et à mesure que la main s’éloigne de l’extrémité ouverte, car cette main restreint l’angle solide disponible pour le rayonnement et augmente ainsi l’effet d’extrémité (ou correction d’extrémité). La longueur du col est augmentée d’un effet d’extrémité chicane et d’un effet d’extrémité non chicane, ce qui lui donne une longueur effective de 0,105 m. Avec une vitesse du son de 343 m/s, l’expression ci-dessus donne une fréquence de résonance de 90 Hz. |
|
Résonances de Helmholtz et guitares
* J’ai dit plus haut que l’air dans le corps d’une guitare agit presque comme un oscillateur de Helmholtz. Ce cas est compliqué parce que le corps peut gonfler un peu lorsque la pression de l’air augmente à l’intérieur – et aussi parce que l’air » dans » la caisse de résonance de la guitare a une géométrie moins facile à visualiser que celle du goulot d’une bouteille. En effet, dans le cas du corps de la guitare, la longueur du bouchon de l’air est approximativement égale aux deux « effets terminaux » à l’extrémité d’un « tuyau » qui n’a que quelques mm d’épaisseur. Les effets terminaux, cependant, sont liés au rayon du trou et de taille similaire, de sorte que la masse d’air est substantielle. La longueur de l’effet final d’un tuyau cylindrique qui débouche sur une chicane plane et infinie est égale à 0,85 fois le rayon du tuyau. Bien que la table d’harmonie d’une guitare ne soit pas infinie, on peut s’attendre à un effet final similaire, et donc la longueur effective du « bouchon » d’air serait d’environ 1,7 fois le rayon du trou. (Certains fabricants augmentent cette valeur en fixant un court tube sous la rosace, de rayon égal).
Quelques personnes ont écrit pour demander quelle devrait être la taille de la caisse de résonance pour un instrument donné. Eh bien, nous pouvons utiliser l’équation ci-dessus pour commencer à répondre à cette question. Cependant, le gonflement du corps est important. Il rend le « ressort » de l’air plus souple et abaisse ainsi la fréquence. La résonance de Helmholtz pure peut être étudiée en maintenant le volume du corps constant. Lors de cette mesure, une pratique courante consiste à enterrer la guitare dans du sable, afin d’empêcher le gonflement ou la « respiration » de la caisse. Cependant, les guitares ne sont généralement pas jouées dans cette situation. Donc le calcul de Helmholtz donnera une surestimation de la fréquence de résonance pour un corps réel et flexible.
Supposons un trou de son circulaire de rayon r, donc S = πr2, et L = 1,7r comme expliqué ci-dessus. Lorsque nous substituons dans l’équation pour la fréquence de Helmholtz, en utilisant c = 340 m/s, nous obtenons :
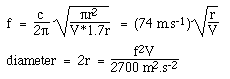
Remarquez que nous utilisons les unités SI standard : nous avons utilisé la vitesse du son en mètres et en secondes, donc le volume doit être en mètres cubes et la fréquence en Hertz, pour donner une réponse en mètres.
C’est plus compliqué lorsque les trous de son ne sont pas circulaires, car l’effet final n’est pas égal à celui d’un cercle de même surface. Le doctorant et luthier John McLennan rédige un rapport de quelques mesures à ce sujet, que nous publierons ici bientôt.
Sur les instruments de la famille des guitares et des violons, la résonance de Helmholtz (plus le corps) est souvent proche ou un peu en dessous de la fréquence de la deuxième corde la plus grave, autour du ré sur un violon ou du sol-la sur une guitare. Vous pouvez réduire ou décaler considérablement la fréquence de Helmholtz en couvrant tout ou partie du trou avec un morceau de carton rigide de forme appropriée. Si vous jouez ensuite une note proche de la résonance et que vous faites glisser le carton pour qu’il couvre et révèle alternativement le trou, vous entendrez clairement l’effet de la résonance.
L’effet de 0,85r est-il raisonnable ? Ra Inta, qui a fait un doctorat sur l’acoustique de la guitare dans notre laboratoire, suggère une démonstration intéressante :
Humidifiez les cordes de votre guitare pour qu’elles ne vibrent pas (par exemple, un mouchoir entre les cordes et la touche). Tenez la paume d’une main au-dessus de la rosace, et tout près de celle-ci. Avec un doigt de l’autre main, frappez la table d’harmonie d’un coup sec près de la rosace et près de la 1ère corde. Vous sentirez une pulsation d’air sur la paume de votre main. Le coup de votre doigt pousse la table d’harmonie vers l’intérieur et expulse un peu d’air du corps. Maintenant, éloignez progressivement votre main du trou, et continuez à taper avec le doigt. Quand cessez-vous de sentir le mouvement de l’air ? Cela vous donnera une estimation approximative de la longueur de « l’effet final » dans le cas du trou de son.
Tuning the Helmholtz resonance
Parmi les publications de John McLennan, doctorant dans ce laboratoire, figure un article dans lequel il fait varier la résonance de Helmholtz en faisant varier la vitesse du son.
- McLennan, J.E. (2003) « A0 and A1 studies on the violin using CO2, He, and air/helium mixtures. » Acustica, 89, 176-180.
Quelques photos de résonateurs de Helmholtz historiques fournies par Thomas B. Greenslade, Kenyon College, Ohio.
Leave a Reply