Qu’est-ce que la géométrie analytique ?
Qu’est-ce que la géométrie analytique ?
La géométrie analytique est une branche de l’algèbre qui est utilisée pour modéliser des objets géométriques – les points, les lignes (droites) et les cercles étant les plus basiques d’entre eux. La géométrie analytique est une grande invention de Descartes et Fermat.
En géométrie analytique plane, les points sont définis comme des paires ordonnées de nombres, disons (x, y), tandis que les lignes droites sont à leur tour définies comme les ensembles de points qui satisfont des équations linéaires, voir les excellentes expositions de D. Pedoe ou D. Brannan et al. Du point de vue de la géométrie analytique, les axiomes géométriques sont des théorèmes dérivables. Par exemple, pour deux points distincts (x1, y1) et (x2, y2), il existe une seule droite ax + by + c = 0 qui passe par ces points. Ses coefficients a, b, c peuvent être trouvés (jusqu’à un facteur constant) à partir du système linéaire de deux équations
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
ou directement de l’équation du déterminant
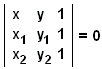 |
Cependant, aucune théorie axiomatique ne peut s’échapper en utilisant des éléments indéfinis. Dans la théorie des ensembles qui sous-tend une grande partie des mathématiques et, en particulier, la géométrie analytique, la notion la plus fondamentale d’ensemble reste indéfinie.
La géométrie de l’espace tridimensionnel est modélisée par des triplets de nombres (x, y, z) et une équation linéaire 3D ax + by + cz + d = 0 définit un plan. En général, la géométrie analytique fournit un outil pratique pour travailler dans des dimensions supérieures.
Dans le cadre de la géométrie analytique, on peut (et on le fait) modéliser également des géométries non euclidiennes. Par exemple, en géométrie projective plane, un point est un triple de coordonnées homogènes (x, y, z), toutes différentes de 0, tel que
| (tx, ty, tz) = (x, y, z), |
pour tout t ≠ 0, tandis qu’une droite est décrite par une équation homogène
| ax + bx + cz = 0. |
En géométrie analytique, les sections coniques sont définies par des équations du second degré :
| ax² + bxy + cy² + dx + ey + f = 0. |
Cette partie de la géométrie analytique qui traite principalement des équations linéaires est appelée algèbre linéaire.
La géométrie analytique cartésienne est une géométrie dans laquelle les axes x = 0 et y = 0 sont perpendiculaires.
Les composantes du n-tuple x = (x1, …, xn) sont appelées ses coordonnées. Lorsque n = 2 ou n = 3, la première coordonnée est appelée abscisse et la seconde ordonnée.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry : A Comprehensive Course, Dover, 1988
|Contact||Front page||Contents||Geometry||Up|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply