Articles /

Processus de Gram-Schmidt

par Marco Taboga, PhD

Le processus (ou procédure) de Gram-Schmidt est une séquence d’opérations qui permettent de transformer un ensemble de vecteurs linéairement indépendants en un ensemble de vecteurs orthonormés qui couvrent le même espace que l’ensemble original.

Table des matières

Préliminaires

Passons en revue quelques notions indispensables à la compréhension du procédé de Gram-Schmidt.

Rappelons que deux vecteurs $r$ et $s$ sont dits orthogonaux si et seulement si leur produit interne est égal à zéro, c’est-à-dire,

Étant donné un produit interne, nous pouvons définir la norme (longueur) d’un vecteur $s$ comme suit :

Un ensemble de vecteurs est dit orthonormé si et seulement si ses éléments ont une norme unitaire et sont orthogonaux entre eux. En d’autres termes, un ensemble de K vecteurs est orthonormé si et seulement si

Nous avons prouvé que les vecteurs d’un ensemble orthonormé sont linéairement indépendants.

Lorsqu’une base pour un espace vectoriel est aussi un ensemble orthonormé, on l’appelle une base orthonormée.

Projections sur des ensembles orthonormés

Dans le processus de Gram-Schmidt, nous utilisons de manière répétée la proposition suivante, qui montre que tout vecteur peut être décomposé en deux parties : 1) sa projection sur un ensemble orthonormé et 2) un résidu qui est orthogonal à l’ensemble orthonormé donné.

Proposition Soit $S$ un espace vectoriel équipé d’un produit interne . Soit un ensemble orthonormé. Pour tout $sin S$, on aoù $arepsilon _{S}$ est orthogonal à $u_{k}$ pour tout $k=1,ldots ,K.$

Proof

DefineAlors, pour chaque $j=1,ldots ,K$, on a queoù : dans les étapes $rame{A}$ et $rame{B}$ nous avons utilisé le fait que le produit interne est linéaire en son premier argument ; à l’étape $rame{C}$ nous avons utilisé le fait que si $keq j$ puisque nous avons affaire à un ensemble orthonormé ; à l’étape $rame{D}$ nous avons utilisé le fait que la norme de $u_{j}$ est égale à 1. Donc, $arepsilon _{S}$, tel que défini ci-dessus, est orthogonal à tous les éléments de l’ensemble orthonormé, ce qui prouve la proposition.

Le terme est appelé la projection linéaire de $s$ sur l’ensemble orthonormé , tandis que le terme $arepsilon _{S}$ est appelé le résidu de la projection linéaire.

Normalisation

Un autre fait peut-être évident que nous allons utiliser à plusieurs reprises dans le processus de Gram-Schmidt est que, si nous prenons un vecteur non nul quelconque et que nous le divisons par sa norme, alors le résultat de la division est un nouveau vecteur qui a une norme unitaire.

En d’autres termes, si alors, par la propriété de définitude de la norme, nous avons que

En conséquence, nous pouvons définiret, par la positivité et l’homogénéité absolue de la norme, on a

Overview de la procédure

Maintenant que nous savons comment normaliser un vecteur et comment le décomposer en une projection sur un ensemble orthonormé et un résidu, nous sommes prêts à expliquer la procédure de Gram-Schmidt.

Nous allons donner un aperçu du processus, après quoi nous l’exprimerons formellement comme une proposition et nous discuterons de tous les détails techniques dans la preuve de la proposition.

Voici l’aperçu.

On nous donne un ensemble de vecteurs linéairement indépendants .

Pour commencer le processus, on normalise le premier vecteur, c’est-à-dire qu’on définit

Dans un deuxième temps, on projette $s_{2}$ sur $u_{1}$:où $arepsilon _{2}$ est le résidu de la projection.

Ensuite, on normalise le résidu :

On prouvera plus tard que (pour que la normalisation puisse être effectuée) car les vecteurs de départ sont linéairement indépendants.

Les deux vecteurs $u_{1}$ et $u_{2}$ ainsi obtenus sont orthonormés.

Dans la troisième étape, on projette $s_{3}$ sur $u_{1}$ et $u_{2}$:et on calcule le résidu de la projection $arepsilon _{3}$.

On le normalise ensuite :

On procède ainsi jusqu’à obtenir le dernier résidu normalisé $u_{K} $.

A la fin du processus, les vecteurs forment un ensemble orthonormé car :

  1. ils sont le résultat d’une normalisation, et par conséquent ils ont une norme unitaire ;

  2. chaque $u_{k}$ est obtenu à partir d’un résidu qui a la propriété d’être orthogonal à .

Pour compléter cet aperçu, rappelons que l’étendue linéaire de est l’ensemble de tous les vecteurs qui peuvent s’écrire comme des combinaisons linéaires de ; elle est notée paret c’est un espace linéaire.

Puisque les vecteurs sont des combinaisons linéairement indépendantes de , tout vecteur qui peut s’écrire comme une combinaison linéaire de peut aussi s’écrire comme une combinaison linéaire de . Par conséquent, les étendues des deux ensembles de vecteurs coïncident:

Énoncé formel

Nous formalisons ici le processus de Gram-Schmidt sous la forme d’une proposition, dont la preuve contient tous les détails techniques de la procédure.

Proposition Soit $S$ un espace vectoriel équipé d’un produit interne . Soit des vecteurs linéairement indépendants. Alors, il existe un ensemble de vecteurs orthonormaux tel quepour tout $kleq K$.

Preuve

La preuve se fait par induction : on prouve d’abord que la proposition est vraie pour $k=1$, puis on prouve qu’elle est vraie pour un k générique si elle vaut pour $k-1$. Lorsque $k=1$, le vecteura la norme unitaire et il constitue à lui seul un ensemble orthonormé : il n’y a pas d’autres vecteurs, donc la condition d’orthogonalité est trivialement satisfaite. L’ensemble est l’ensemble de tous les multiples scalaires de $s_{1}$, qui sont aussi des multiples scalaires de $u_{1}$ (et vice versa). Par conséquent, Maintenant, supposons que la proposition soit vraie pour $k-1$. Alors, on peut projeter $s_{k}$ sur :où le résidu $arepsilon _{k}$ est orthogonal à . Supposons que $arepsilon _{k}=0$. Alors,Puisque, par hypothèse, pour tout $jleq k-1$, on a que pour tout $jleq k-1$, où $lpha _{jl}$ sont des scalaires. Donc,En d’autres termes, l’hypothèse que $arepsilon _{k}=0$ conduit à la conclusion que $s_{k}$ est une combinaison linéaire de . Mais c’est impossible car l’une des hypothèses de la proposition est que sont linéairement indépendants. En conséquence, il faut que . Nous pouvons donc normaliser le résidu et définir le vecteur qui a une norme unitaire. Nous savons déjà que $arepsilon _{k}$ est orthogonal à . Cela implique que également $u_{k}$ est orthogonal à . Ainsi, est un ensemble orthonormé. Maintenant, prenons un vecteur quelconque $sin S$ qui peut être écrit sous la formeoù sont des scalaires. 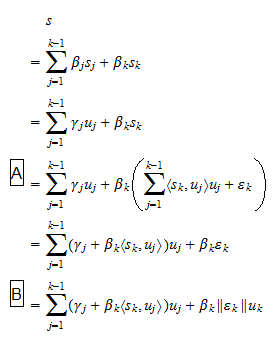Puisque, par hypothèse, nous avons que l’équation (2) peut aussi s’écrire sous la formeoù sont des scalaires, et : à l’étape $rame{A}$ nous avons utilisé l’équation (1) ; à l’étape $rame{B}$ nous avons utilisé la définition de $u_{k}$. Ainsi, nous avons prouvé que tout vecteur qui peut être écrit comme une combinaison linéaire de peut aussi être écrit comme une combinaison linéaire de . L’hypothèse (3) permet de prouver la réciproque de manière tout à fait analogue :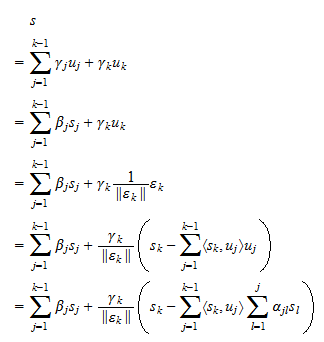En d’autres termes, toute combinaison linéaire de est aussi une combinaison linéaire de . Ceci prouve que et conclut la preuve.

Tout espace de produit interne a une base orthonormée

La proposition suivante présente une conséquence importante du procédé de Gram-Schmidt.

Proposition Soit $S$ un espace vectoriel muni d’un produit interne . Si $S$ a une dimension finie , alors il existe une base orthonormée pour $S$.

Proof

Puisque $S$ est de dimension finie, il existe au moins une base pour $S$, constituée de K vecteurs . On peut appliquer la procédure de Gram-Schmidt à cette base et obtenir un ensemble orthonormé . Puisque est une base, elle s’étend sur $S$. Par conséquent, 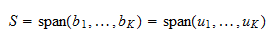Donc, est une base orthonormée de $S$.

Exercices résolus

Vous trouverez ci-dessous quelques exercices avec des solutions expliquées.

Exercice 1

Considérons l’espace $S$ de tous les $3imes 1$ vecteurs ayant des entrées réelles et le produit interneoù $r,sin S$ et $s^{op }$ est la transposition de $s$. Définir le vecteur

Normaliser $s$.

Solution

La norme de $s$ estDonc, la normalisation de $s$ est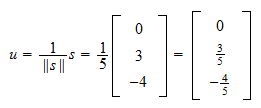

Exercice 2

Considérons l’espace $S$ de tous les $2imes 1$ vecteurs ayant des entrées réelles et le produit interneoù $r,sin S$ . Considérons les deux vecteurs linéairement indépendants

Transformons-les en un ensemble orthonormé en utilisant le procédé de Gram-Schmidt.

Solution

La norme de $s_{1}$ est Donc, le premier vecteur orthonormé estLe produit interne de $s_{2}$ et $u_{1}$ est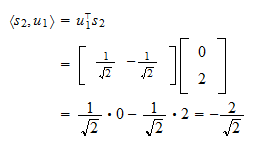La projection de $s_{2}$ sur $u_{1}$ est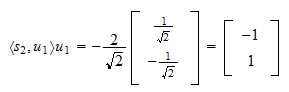Le résidu de la projection est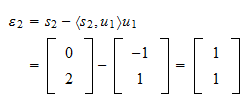La norme du résidu estet le résidu normalisé estDonc, l’ensemble orthonormal que nous recherchions est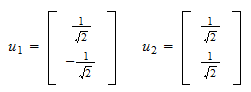

Comment citer

Veuillez citer comme :

Taboga, Marco (2017).  » Processus de Gram-Schmidt « , Lectures on matrix algebra. https://www.statlect.com/matrix-algebra/Gram-Schmidt-process.

Leave a Reply