Partie 14 : Produit de points et produit d’Hadamard

Outre la multiplication matricielle abordée précédemment, les vecteurs pourraient être multipliés par deux autres méthodes : Le produit scalaire et le produit Hadamard. Les résultats obtenus par ces deux méthodes sont différents.

Les éléments correspondant à la même ligne et à la même colonne sont multipliés ensemble et les produits sont additionnés de telle sorte que, le résultat est un scalaire.

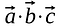
À la différence de la multiplication matricielle, le résultat du produit scalaire n’est pas un autre vecteur ou une autre matrice, c’est un scalaire.

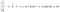
L’ordre des vecteurs n’a pas d’importance pour le produit scalaire, il suffit que le nombre d’éléments des deux vecteurs soit égal.

La formule géométrique du produit scalaire est

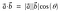
Le produit scalaire est aussi appelé produit interne ou produit scalaire.

Projection de vecteur

Supposons que nous ayons deux vecteurs c et d, sous-tendus par l’angle, phi(Ф).

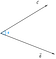
Maintenant, la projection du vecteur c sur le vecteur d pourrait être représentée comme

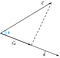
Nous pouvons conclure de la figure que la projection est égale à la composante horizontale du vecteur c par rapport à l’angle phi(Ф).

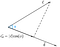
C’est ce qu’on appelle la projection scalaire.Pour trouver la projection vectorielle du vecteur c sur le vecteur d, nous devons multiplier la projection scalaire par le vecteur unitaire d.

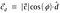
Substituer la valeur du vecteur unitaire d.

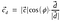
Donc, le produit scalaire peut également être représenté par

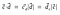
Les projections sont largement utilisées en algèbre linéaire et en apprentissage automatique (le Support Vector Machine(SVM) est un algorithme d’apprentissage automatique, utilisé pour la classification des données).

Produit d’Hadamard (Multiplication par éléments)

Le produit d’Hadamard de deux vecteurs est très similaire à l’addition de matrices, les éléments correspondant aux mêmes lignes et colonnes de vecteurs/matrices donnés sont multipliés ensemble pour former un nouveau vecteur/matrice.

Il est nommé d’après le mathématicien français, Jacques Hadamard.

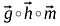
L’ordre des matrices/vecteurs à multiplier doit être le même et la matrice résultante sera également du même ordre.

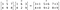
Le produit de Hadamard est utilisé dans les techniques de compression d’images comme le JPEG. Il est également connu sous le nom de produit de Schur, d’après le mathématicien allemand, Issai Schur.

Le produit de Hadamard est utilisé dans les cellules LSTM (mémoire à long terme) des réseaux neuronaux récurrents (RNN).

.