Mathématiques pour les arts libéraux

En plus de l’autosimilarité visuelle, les fractales présentent d’autres propriétés intéressantes. Par exemple, remarquez que chaque étape de l’itération du joint de Sierpinski supprime un quart de la surface restante. Si ce processus est poursuivi indéfiniment, nous finirions par supprimer essentiellement toute la zone, ce qui signifie que nous avons commencé avec une zone à 2 dimensions et que nous finissons en quelque sorte avec quelque chose de moins que cela, mais apparemment plus qu’une simple ligne à 1 dimension.

Pour explorer cette idée, nous devons discuter de la dimension. Quelque chose comme une ligne est 1-dimensionnelle ; elle n’a que la longueur. Toute courbe est 1-dimensionnelle. Les choses comme les boîtes et les cercles sont 2-dimensionnelles, puisqu’elles ont une longueur et une largeur, décrivant une surface. Les objets comme les boîtes et les cylindres ont une longueur, une largeur et une hauteur, décrivant un volume, et sont à 3 dimensions.

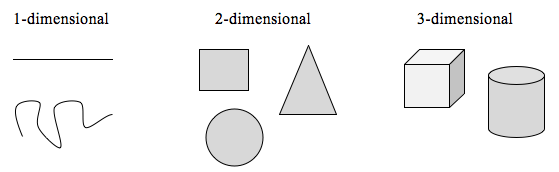
Certaines règles s’appliquent pour la mise à l’échelle des objets, liées à leur dimension.

Si j’avais une ligne de longueur 1, et que je voulais mettre sa longueur à l’échelle par 2, j’aurais besoin de deux copies de la ligne originale. Si j’avais une ligne de longueur 1, et que je voulais mettre sa longueur à l’échelle par 3, j’aurais besoin de trois copies de l’original.

Si j’avais un rectangle de longueur 2 et de hauteur 1, et que je voulais mettre à l’échelle sa longueur et sa largeur par 2, j’aurais besoin de quatre copies du rectangle original. Si je voulais mettre à l’échelle la longueur et la largeur par 3, j’aurais besoin de neuf copies du rectangle original.

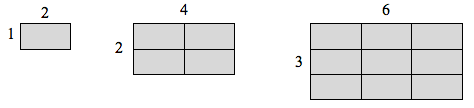
Si j’avais une boîte cubique avec des côtés de longueur 1, et que je voulais mettre à l’échelle sa longueur et sa largeur par 2, j’aurais besoin de huit copies du cube original. Si je voulais mettre à l’échelle la longueur et la largeur par 3, j’aurais besoin de 27 copies du cube original.

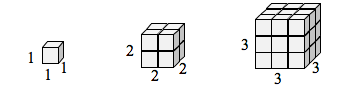
Notez que dans le cas 1-dimensionnel, les copies nécessaires = échelle.

Dans le cas 2-dimensionnel, les copies nécessaires = échelle^{2}.

Dans le cas 3-dimensionnel, les copies nécessaires = échelle^{3}.

De ces exemples, on pourrait déduire un modèle.

Exemple

Utiliser la relation échelle-dimension pour déterminer la dimension du joint de Sierpinski.

Supposons que nous définissions le joint original comme ayant une longueur de côté de 1. Le plus grand joint représenté est deux fois plus large et deux fois plus haut, il a donc été mis à l’échelle par un facteur 2.

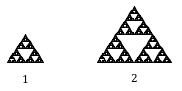
Notez que pour construire le plus grand joint, 3 copies du joint original sont nécessaires.

En utilisant la relation échelle-dimension C=S^{D}, on obtient l’équation 3=2^{D}.

Puisque 2^{1}=2 et 2^{2}=4, nous pouvons immédiatement voir que D est quelque part entre 1 et 2 ; le joint est plus qu’une forme à 1 dimension, mais nous avons enlevé tellement de surface qu’elle est maintenant moins que 2 dimensions.

La résolution de l’équation 3=2^{D} nécessite des logarithmes. Si vous avez étudié les logarithmes précédemment, vous vous souvenez peut-être de la façon de résoudre cette équation (sinon, passez simplement à l’encadré ci-dessous et utilisez cette formule avec la touche log d’une calculatrice) :

Prenez le logarithme des deux côtés.

3={2}^{D}}

Utilisez la propriété d’exposant des logarithmes.

\Log(3)=\log(2}^{D}}(droite)

Diviser par log(2).

\log(3)=D\log\\left(2\right)

La dimension du joint est d’environ 1,585.

D=\frac{\log\left(3\right)}{\log(2)}\approx1.585

Try It

Déterminer la dimension fractale de la fractale produite en utilisant l’initiateur et le générateur.

Afficher la solution

La mise à l’échelle de la fractale par un facteur 3 nécessite 5 copies de l’original.

D=\frac{\text{log}\left(5\right)}{\text{log}\left(3\right)}\approx1,465

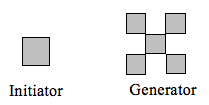
Dans la vidéo suivante, nous présentons un exemple travaillé de la façon de déterminer la dimension du joint de Sierpinski

.