Introduction au hachage cohérent

Avec l’essor des architectures distribuées, le hachage cohérent est devenu courant. Mais de quoi s’agit-il exactement et en quoi est-il différent d’un algorithme de hachage standard ? Quelles sont les motivations exactes qui le sous-tendent ?

D’abord, nous décrirons les principaux concepts. Ensuite, nous creuserons les algorithmes existants pour comprendre les défis associés au hachage cohérent.

Hachage

Le hachage est le processus permettant de faire correspondre des données de taille arbitraire à des valeurs de taille fixe. Chaque algorithme existant a sa propre spécification:

• MD5 produit des valeurs de hachage de 128 bits.
• SHA-1 produit des valeurs de hachage de 160 bits.
• etc.

Le hachage a de nombreuses applications en informatique. Par exemple, l’une de ces applications est appelée somme de contrôle. Pour vérifier l’intégrité d’un jeu de données, il est possible d’utiliser un algorithme de hachage. Un serveur procède au hachage d’un ensemble de données et indique la valeur de hachage à un client. Ensuite, le client hache sa version du jeu de données et compare les valeurs de hachage. Si elles sont égales, l’intégrité devrait être vérifiée.

Le « devrait » ici est important. Le pire scénario est lorsqu’une collision se produit. Une collision, c’est lorsque deux données distinctes ont la même valeur de hachage. Prenons un exemple concret en définissant la fonction de hachage suivante : étant donné une personne, elle renvoie sa date d’anniversaire (jour & mois de naissance). Le paradoxe de l’anniversaire nous dit que si nous n’avons que 23 personnes dans une pièce, la probabilité que deux personnes aient le même anniversaire (donc une collision) est supérieure à 50%. Par conséquent, la fonction anniversaire n’est probablement pas une bonne fonction de hachage.

Pour une introduction rapide sur le hachage, il est important de comprendre que l’idée principale est de répartir des valeurs dans un domaine. Par exemple :

• MD5 répartit les valeurs sur un domaine spatial de 128 bits
• Une table de hachage (ou hashmap) soutenue par un tableau de 32 éléments a une fonction de hachage interne qui répartit les valeurs sur n’importe quel indice (de 0 à 31).

Distribution de la charge

La distribution de la charge peut être définie comme le processus de répartition de la charge sur les nœuds. Le terme nœud est ici interchangeable avec serveur ou instance. C’est une unité de calcul.

L’équilibrage de charge est un exemple de distribution de charge. Il s’agit de répartir un ensemble de tâches sur un ensemble de ressources. Par exemple, nous utilisons l’équilibrage de charge pour distribuer les demandes d’API entre les instances de serveur web.

Lorsqu’il s’agit de données, nous utilisons plutôt le terme sharding. Un sharding de base de données est une partition horizontale des données dans une base de données. Un exemple typique est une base de données partitionnée en trois shards où chaque shard possède un sous-ensemble des données totales.

L’équilibrage de charge et le sharding partagent certains défis communs. Répartir uniformément les données par exemple pour garantir qu’un nœud n’est pas surchargé par rapport aux autres. Dans certains contextes, l’équilibrage de charge et le sharding doivent également continuer à associer des tâches ou des données au même nœud :

• Si nous devons sérialiser, traiter une par une, les opérations pour un consommateur donné, nous devons acheminer la requête vers le même nœud.
• Si nous devons distribuer des données, nous devons savoir quel shard est le propriétaire pour une clé particulière.

Cela vous semble familier ? Dans ces deux exemples, nous répartissons des valeurs sur un domaine. Que ce soit une tâche répartie sur les nœuds du serveur ou des données réparties sur le shard de la base de données, nous retrouvons l’idée associée au hachage. C’est la raison pour laquelle le hachage peut être utilisé conjointement avec la répartition de la charge. Voyons comment.

Mod-n Hashing

Le principe du hashing mod-n est le suivant . Chaque clé est hachée en utilisant une fonction de hachage pour transformer une entrée en un entier. Ensuite, on effectue un modulo basé sur le nombre de nœuds.

Voyons un exemple concret avec 3 nœuds. Ici, nous devons répartir la charge entre ces nœuds en fonction d’un identifiant de clé. Chaque clé est hachée puis nous effectuons une opération modulo :

L’avantage de cette approche est son caractère apatride. Nous n’avons pas besoin de conserver d’état pour nous rappeler que foo a été acheminé vers le nœud 2. Pourtant, nous devons savoir combien de nœuds sont configurés pour appliquer l’opération modulo.

Alors, comment le mécanisme fonctionne-t-il en cas de passage à l’échelle (ajout ou suppression de nœuds) ? Si nous ajoutons un autre nœud, l’opération modulo est maintenant basée sur 4 au lieu de 3:

Comme nous pouvons le voir, les clés foo et baz ne sont plus associées au même nœud. Avec le hachage mod-n, il n’y a aucune garantie de maintenir une quelconque cohérence dans l’association clé/nœud. Cela pose-t-il un problème ? Cela pourrait.

Que se passe-t-il si nous mettons en œuvre un datastore utilisant le sharding et basé sur la stratégie mod-n pour distribuer les données ? Si nous faisons évoluer le nombre de nœuds, nous devons effectuer une opération de rééquilibrage. Dans l’exemple précédent, le rééquilibrage signifie :

• Déplacer foo du nœud 2 au nœud 0.
• Déplacer baz du nœud 2 au nœud 3.

Maintenant, que se passe-t-il si nous avions stocké des millions, voire des milliards de données et que nous devions presque tout rééquilibrer ? Comme nous pouvons l’imaginer, ce serait un processus lourd. Par conséquent, nous devons modifier notre technique de distribution de la charge pour nous assurer que lors du rééquilibrage :

• La distribution restent aussi uniforme que possible en fonction du nouveau nombre de nœuds.
• Le nombre de clés que nous devons migrer devrait être limité. Idéalement, il ne serait que de 1/n pour cent des clés où n est le nombre de nœuds.

C’est exactement le but des algorithmes de hachage cohérents.

Le terme cohérent pourrait cependant prêter à confusion. J’ai rencontré des ingénieurs qui supposaient que de tels algorithmes continuaient à associer une clé donnée au même nœud même face à l’évolutivité. Ce n’est pas le cas. Il doit être cohérent jusqu’à un certain point pour garder la distribution uniforme.

Maintenant, il est temps de creuser dans certaines solutions.

Rendezvous

Rendezvous a été le premier algorithme jamais proposé pour résoudre notre problème. Bien que l’étude originale, publiée en 1996, ne mentionne pas le terme de hachage cohérent, elle fournit une solution aux défis que nous avons décrits. Voyons une implémentation possible en Go:

Comment cela fonctionne-t-il ? Nous traversons chaque nœud et nous calculons sa valeur de hachage. La valeur de hachage est retournée par une fonction hash qui produit un entier basé sur une clé (notre entrée) et un identifiant de nœud (l’approche la plus simple est de hacher la concaténation des deux chaînes). Ensuite, nous retournons le nœud avec la valeur de hachage la plus élevée. C’est la raison pour laquelle l’algorithme est également connu sous le nom de hachage de poids aléatoire le plus élevé.

Le principal inconvénient de rendezvous est sa complexité temporelle O(n) où n est le nombre de nœuds. Il est très efficace si nous avons besoin d’avoir un nombre limité de nœuds. Pourtant, si nous commençons à maintenir des milliers de nœuds, il pourrait commencer à causer des problèmes de performance.

Ring Consistent Hash

L’algorithme suivant a été publié en 1997 par Karger et al. dans cet article. Cette étude a mentionné pour la première fois le terme de hachage cohérent.

Il est basé sur un anneau (un tableau connecté de bout en bout). Bien qu’il s’agisse de l’algorithme de hachage cohérent le plus populaire (ou du moins le plus connu), son principe n’est pas toujours bien compris. Plongeons-y.

La première opération consiste à créer l’anneau. Un anneau a une longueur fixe. Dans notre exemple, nous le partitionnons en 12 parties :

Puis, nous positionnons nos nœuds. Dans notre exemple, nous définirons N0, N1 et N2.

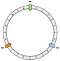
Les nœuds sont répartis uniformément pour le moment. Nous reviendrons sur ce point plus tard.

Alors, il est temps de voir comment représenter les clés. Tout d’abord, nous avons besoin d’une fonction f qui renvoie un indice d’anneau (de 0 à 11) basé sur une clé. Nous pouvons utiliser le hachage mod-n pour cela. Comme la longueur de l’anneau est constante, cela ne nous posera aucun problème.

Dans notre exemple, nous allons définir 3 clés : a, b et c. Nous appliquons f sur chacune d’elles. Supposons que nous ayons les résultats suivants:

• f(a) = 1
• f(a) = 5
• f(a) = 7

On peut donc positionner les clés sur l’anneau de cette façon :

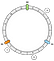
Comment associer une clé donnée à un nœud ? La logique principale est d’avancer. A partir d’une clé donnée, nous retournons le premier nœud que nous trouvons ensuite tout en progressant vers l’avant :

Dans cet exemple, nous associons a à N1, b et c à N2.

Maintenant, voyons comment le rééquilibrage est géré. Nous définissons un autre nœud N3. Où devons-nous le positionner ? Il n’y a plus d’espace pour que la distribution globale soit uniforme. Devons-nous réorganiser les nœuds ? Non, sinon nous ne serions plus cohérents, n’est-ce pas ? Pour positionner un nœud, nous réutilisons la même fonction de hachage f que nous avons introduite. Au lieu d’être appelée avec une clé, elle peut être appelée avec un identifiant de nœud. Ainsi, la position du nouveau nœud est décidée aléatoirement.

Une question se pose alors : que faire de a puisque le prochain nœud n’est plus N1:

La solution est la suivante : nous devons changer son association et obtenir que a soit associé à N3:

Comme nous l’avons vu précédemment, un algorithme idéal devrait rééquilibrer 1/n pour cent des clés en moyenne. Dans notre exemple, comme nous ajoutons un quatrième nœud, nous devrions avoir 25% des clés possibles réassociées à N3. Est-ce le cas ?

• N0 des indices 8 à 12 : 33,3% du total des clés
• N1 des indices 2 à 4 : 16,6% du total des clés
• N2 des indices 4 à 8 : 33.3% du total des clés
• N3 des indices 0 à 2 : 16,6% du total des clés

La distribution elle n’est pas uniforme. Comment pouvons-nous l’améliorer ? La solution est d’utiliser des nœuds virtuels.

Disons qu’au lieu de positionner un seul spot par nœud, nous pouvons en positionner trois. Aussi, nous devons définir trois fonctions de hachage différentes. Chaque nœud est haché trois fois de sorte que nous obtenons trois indices différents :

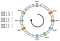
Nous pouvons appliquer le même algorithme en avançant. Pourtant, une clé serait associée à un nœud indépendamment du nœud virtuel qu’il a rencontré.

Dans ce même exemple, la distribution serait maintenant la suivante :

• N0 : 33,3%
• N1 : 25%
• N2 : 41,6%

Plus on définit de nœuds virtuels par nœud, plus la distribution devrait être uniforme. En moyenne, avec 100 nœuds virtuels par serveur, la distribution standard est d’environ 10%. Avec 1000, elle est d’environ 3,2%.

Ce mécanisme est également utile si nous avons des nœuds de taille différente. Par exemple, si un nœud est configuré pour gérer théoriquement deux fois la charge que les autres, nous pourrions faire tourner deux fois plus de nœuds virtuels.

Pour autant, le principal inconvénient avec les nœuds virtuels est l’empreinte mémoire. Si nous devons gérer des milliers de serveurs, cela nécessiterait des mégaoctets de mémoire.

Avant de passer à autre chose, il est intéressant de noter que parfois un algorithme peut être considérablement amélioré en changeant une petite partie. C’est le cas par exemple d’un algorithme publié par Google en 2017 appelé hachage cohérent avec charges bornées. Cette version est basée sur la même idée d’anneau que nous avons décrite. Pourtant, leur approche consiste à effectuer un petit rééquilibrage lors de toute mise à jour (une nouvelle clé ou un nœud ajouté/supprimé). Cette version surpasse la version originale en termes d’écart type avec le compromis d’une pire complexité temporelle.

Jump Consistent Hash

En 2007, deux ingénieurs de Google ont publié jump consistent hash. Par rapport à l’algorithme basé sur l’anneau, cette mise en œuvre « ne nécessite pas de stockage, est plus rapide et fait un meilleur travail de division égale de l’espace de clé entre les seaux et de division égale de la charge de travail lorsque le nombre de seaux change ». Dit autrement, il améliore la distribution de la charge de travail entre les nœuds (un bucket est le même concept qu’un nœud) sans aucune surcharge de mémoire.

Voici l’algorithme en C++ (7 lignes de code 🤯):

Dans le hachage cohérent en anneau, avec 1000 nœuds virtuels, l’écart type était d’environ 3,2%. En jump consistent hash, nous n’avons plus besoin de la notion de nœuds virtuels. Pourtant, l’écart-type reste inférieur à 0,0000001%.

Il y a cependant une limitation. Les nœuds doivent être numérotés de manière séquentielle. Si nous avons une liste de serveurs foo, bar et baz, nous ne pouvons pas supprimer bar par exemple. Pourtant, si nous configurons un magasin de données, nous pouvons appliquer l’algorithme pour obtenir l’indice de shard basé sur le nombre total de shards. Par conséquent, le hachage cohérent de saut peut être utile dans le contexte du sharding mais pas de l’équilibrage de charge.

Qu’est-ce que l’algorithme de hachage cohérent parfait ?

Comme nous avons maintenant une certaine expérience du hachage cohérent, prenons un peu de recul et voyons ce que serait l’algorithme parfait :

• Seulement 1/n pour cent des clés seraient remappées en moyenne où n est le nombre de nœuds.
• Une complexité spatiale O(n) où n est le nombre de nœuds.
• Une complexité temporelle O(1) par insertion/suppression d’un nœud et par consultation de clé.
• Un écart type minimal pour s’assurer qu’un nœud n’est pas surchargé par rapport à un autre.
• Il permettrait d’associer un poids à un nœud pour faire face à différents dimensionnements de nœuds.
• Il permettrait un nom arbitraire des nœuds (non numérotés séquentiellement) pour supporter à la fois l’équilibrage de charge et le sharding.

Malheureusement, cet algorithme n’existe pas. Sur la base de ce que nous avons vu:

• Rendezvous a une complexité de temps linéaire par lookup.
• Ring consistent hash a un pauvre écart-type minimal sans le concept de nœuds virtuels. Avec les nœuds virtuels, est complexité spatiale est O(n*v) avec n le nombre de nœuds et v le nombre de nœuds virtuels par nœud.
• Le hachage cohérent par saut n’a pas une complexité temporelle constante et il ne supporte pas le nom arbitraire des nœuds.

Le sujet est toujours ouvert et il y a des études récentes qui valent le coup d’œil. Par exemple, le hachage cohérent multi-sonde sorti en 2005. Il supporte une complexité spatiale O(1). Pourtant, pour obtenir un écart-type de ε, il faut O(1/ε) temps par consultation. Par exemple, si nous voulons obtenir un écart-type inférieur à 0,5 %, il faut hacher la clé environ 20 fois. Par conséquent, nous pouvons obtenir un écart-type minimal mais dans l’effort d’une complexité de temps de consultation plus élevée.

Comme nous l’avons dit dans l’introduction, les algorithmes de hachage cohérents sont devenus courants. Ils sont désormais utilisés dans d’innombrables systèmes tels que MongoDB, Cassandra, Riak, Akka, etc. que ce soit dans le cadre de l’équilibrage de la charge ou de la distribution des données. Pourtant, comme souvent en informatique, chaque solution a des compromis.

En parlant de compromis, si vous avez besoin d’un suivi, vous pouvez jeter un coup d’œil à l’excellent billet écrit par Damian Gryski:

.