Introduction à la déconvolution

La déconvolution est une technique de traitement d’image à forte intensité de calcul qui est de plus en plus utilisée pour améliorer le contraste et la résolution des images numériques capturées au microscope. Les fondements sont basés sur une suite de méthodes qui sont conçues pour supprimer ou inverser le flou présent dans les images de microscope induit par l’ouverture limitée de l’objectif.

Presque toute image acquise sur un microscope à fluorescence numérique peut être déconvoluée, et plusieurs nouvelles applications sont en cours de développement qui appliquent des techniques de déconvolution à des images en lumière transmise recueillies sous une variété de stratégies d’amélioration du contraste. Parmi les sujets les plus appropriés pour l’amélioration par déconvolution, on trouve les montages tridimensionnels construits à partir d’une série de sections optiques.

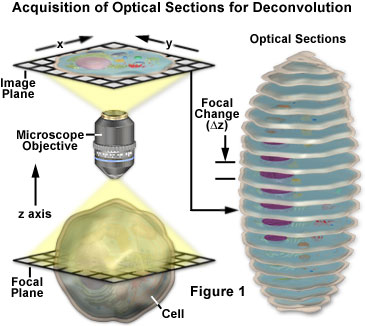
Les concepts de base entourant l’acquisition d’images en série z pour l’analyse par déconvolution sont présentés avec un schéma dans la figure 1. Une série d’images de l’échantillon est enregistrée, chacune étant légèrement décalée l’une par rapport à l’autre le long de l’axe z. Ce changement de plan focal donne une image légèrement différente, avec des changements subtils causés par la lumière hors foyer provenant du dessus et du dessous du plan z actuel. Pendant l’analyse de déconvolution, toute la série z est analysée pour créer un ensemble de données plus claires et de plus haute résolution qui n’est pas alambiqué par la fluorescence hors foyer.

La déconvolution est souvent suggérée comme une bonne alternative au microscope confocal, car les deux techniques cherchent à minimiser l’effet de la fluorescence hors foyer sur votre image finale…. Ceci n’est pas strictement vrai car les images acquises à l’aide d’une ouverture en sténopé dans un microscope confocal bénéficient du traitement de déconvolution. La microscopie confocale empêche la détection de la lumière hors foyer en plaçant une ouverture en trou d’épingle entre l’objectif et le détecteur, à travers laquelle seuls les rayons lumineux focalisés peuvent passer. En revanche, les microscopes à grand champ permettent à la lumière hors foyer de passer directement au détecteur. La déconvolution est ensuite appliquée aux images résultantes pour soustraire la lumière hors foyer ou la réaffecter à sa source. La microscopie confocale est particulièrement bien adaptée à l’examen de spécimens épais tels que les embryons ou les moules, tandis que le traitement de déconvolution grand champ s’est révélé être un outil puissant pour l’imagerie de spécimens nécessitant des niveaux de lumière extrêmement faibles. Ces outils peuvent même être combinés pour réduire le bruit des images acquises sur un microscope confocal. Cependant, une majorité des expériences de déconvolution rapportées dans la littérature s’appliquent aux images enregistrées sur un microscope à fluorescence standard à grand champ.

Sources de dégradation de l’image

La dégradation de l’image peut être divisée en quatre sources indépendantes : le bruit, la diffusion, l’éblouissement et le flou. La figure 2 présente des exemples de l’impact visuel de chacune d’entre elles sur la même image.

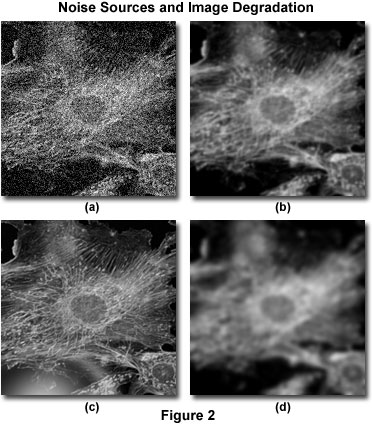
Le bruit peut être décrit comme un désarrangement quasi-aléatoire des détails d’une image, qui (dans sa forme la plus sévère) a l’apparence d’un bruit blanc ou d’un bruit sel et poivre, semblable à ce que l’on voit à la télévision radiodiffusée en cas de mauvaise réception (figure 2(a)). Ce type de bruit est qualifié de « quasi-aléatoire » car sa distribution statistique peut être prédite si l’on connaît les mécanismes de la source. En microscopie numérique, la principale source de bruit est soit le signal lui-même (souvent appelé bruit de photons), soit le système d’imagerie numérique. La mécanique de ces deux sources de bruit est comprise et, par conséquent, la distribution statistique du bruit est connue. Le bruit dépendant du signal peut être caractérisé par une distribution de Poisson, tandis que le bruit provenant du système d’imagerie suit souvent une distribution gaussienne. Parce que la source et la distribution du bruit commun dans les images numériques sont si bien comprises, il peut être facilement éliminé par l’application des filtres d’image appropriés, qui sont généralement inclus dans la plupart des logiciels de déconvolution en tant que routine optionnelle de « prétraitement ».

La diffusion est généralement désignée comme une perturbation aléatoire de la lumière induite par les changements d’indice de réfraction dans tout un spécimen. L’effet net de la diffusion est un désarrangement véritablement aléatoire des détails de l’image, comme le montre la figure 2(b). Bien qu’aucune méthode totalement satisfaisante n’ait été développée pour prédire la diffusion dans un échantillon donné, il a été démontré que le degré de diffusion dépend fortement de l’épaisseur de l’échantillon et des propriétés optiques de l’échantillon et des matériaux d’enrobage environnants. La diffusion augmente à la fois avec l’épaisseur de l’échantillon et l’hétérogénéité de l’indice de réfraction présenté par les composants internes d’un échantillon.

Similaire à la diffusion, l’éblouissement est une perturbation aléatoire de la lumière, mais il se produit dans les éléments optiques (lentilles, filtres, prismes, etc.) du microscope plutôt que dans l’échantillon. Le niveau d’éblouissement dans un microscope moderne a été minimisé par l’utilisation de lentilles et de filtres avec des revêtements antireflets, et par le raffinement des techniques de formation des lentilles, des ciments optiques et des formulations de verre. La figure 2(c) illustre l’effet d’un éblouissement non contrôlé.

Le flou est décrit par une propagation non aléatoire de la lumière qui se produit lors du passage dans le chemin optique du système d’imagerie (figure 2(d)). La source la plus importante de flou est la diffraction, et une image dont la résolution n’est limitée que par le flou est considérée comme limitée par la diffraction. Cela représente une limite intrinsèque de tout système d’imagerie et constitue le facteur déterminant pour évaluer la limite de résolution d’un système optique. Heureusement, il existe des modèles sophistiqués de flou dans un microscope optique qui peuvent être utilisés pour déterminer la source des photons hors foyer. C’est la base de la déconvolution. En raison de son importance fondamentale dans la déconvolution, le modèle théorique du flou sera discuté plus en détail dans d’autres parties de cette section. Cependant, il faut souligner que tous les systèmes d’imagerie produisent du flou indépendamment des autres formes de dégradation de l’image induites par l’échantillon ou l’électronique instrumentale qui l’accompagne. C’est précisément cette indépendance du flou optique par rapport aux autres types de dégradation qui permet la possibilité d’éliminer le flou par des techniques de déconvolution.

L’interaction de la lumière avec la matière est la principale origine physique de la diffusion, de l’éblouissement et du flou. Cependant, la composition et la disposition des molécules dans un matériau donné (qu’il s’agisse de verre, d’eau ou de protéines) confèrent à chaque matériau un ensemble particulier de propriétés optiques. Aux fins de la déconvolution, ce qui distingue la diffusion, l’éblouissement et le flou, c’est l’endroit où ils se produisent et la possibilité de générer un modèle mathématique pour ces phénomènes. La diffusion étant un phénomène localisé et irrégulier se produisant dans l’échantillon, elle s’est avérée difficile à modéliser. En revanche, le flou étant une fonction du système optique du microscope (principalement l’objectif), il peut être modélisé avec une relative simplicité. Un tel modèle rend possible d’inverser mathématiquement le processus de flou, et la déconvolution emploie ce modèle pour inverser ou supprimer le flou.

La fonction d’étalement du point

Le modèle de flou qui a évolué dans l’optique théorique est basé sur le concept d’une fonction d’étalement du point (PSF) tridimensionnelle. Ce concept est d’une importance fondamentale pour la déconvolution et doit être clairement compris afin d’éviter les artefacts d’imagerie. La fonction d’étalement du point est basée sur une source de lumière ponctuelle infiniment petite provenant de l’espace du spécimen (objet). Comme le système d’imagerie du microscope ne recueille qu’une fraction de la lumière émise par ce point, il ne peut pas concentrer la lumière en une image tridimensionnelle parfaite du point. Au lieu de cela, le point apparaît élargi et étalé dans un motif de diffraction tridimensionnel. Ainsi, la fonction d’étalement du point est formellement définie comme le motif de diffraction tridimensionnel généré par une source ponctuelle idéale de lumière.

Selon le mode d’imagerie utilisé (champ large, confocal, lumière transmise), la fonction d’étalement du point a une forme et un contour différents et uniques. Dans un microscope à fluorescence à grand champ, la forme de la fonction d’étalement du point ressemble à celle d’un « football » oblong de lumière entouré d’une fusée d’anneaux qui s’élargissent. Pour décrire la fonction d’étalement du point en trois dimensions, il est courant d’appliquer un système de coordonnées à trois axes (x, y et z) où × et y sont parallèles au plan focal de l’échantillon et z est parallèle à l’axe optique du microscope. Dans ce cas, la fonction d’étalement du point apparaît comme un ensemble d’anneaux concentriques dans le plan x-y, et ressemble à un sablier dans les plans x-z et y-z (comme illustré à la figure 3). Une coupe x-y à travers le centre de la fonction d’étalement du point à grand champ révèle un ensemble d’anneaux concentriques : le disque dit d’Airy qui est couramment référencé dans les textes sur la microscopie optique classique.

Deux projections x-z de fonctions d’étalement du point montrant différents degrés d’aberration sphérique sont présentées sur la figure 3. L’axe optique est parallèle à l’axe vertical de l’image. La fonction d’étalement du point de gauche présente une aberration sphérique minimale, tandis que celle de droite présente un degré d’aberration important. Notez que l’asymétrie axiale et l’élargissement du nœud central le long de l’axe optique dans l’image de droite entraînent une dégradation de la résolution axiale et un flou du signal. En théorie, la taille de la fonction d’étalement du point est infinie, et l’intensité totale additionnée de la lumière dans les plans éloignés du foyer est égale à l’intensité additionnée au foyer. Toutefois, l’intensité lumineuse diminue rapidement et finit par ne plus pouvoir être distinguée du bruit. Dans une fonction d’étalement du point non aberrante enregistrée avec un objectif à immersion dans l’huile à ouverture numérique élevée (1,40), la lumière occupant 0,2 micromètre carré au niveau du foyer est étalée sur 90 fois cette surface à 1 micromètre au-dessus et au-dessous du foyer. Le spécimen utilisé pour enregistrer ces images de fonction d’étalement du point était une perle fluorescente de 0,1 micromètre de diamètre montée dans du glycérol (indice de réfraction égal à 1,47), avec des huiles d’immersion ayant les indices de réfraction notés dans la figure.

Une considération importante est la façon dont la fonction d’étalement du point affecte la formation d’images dans le microscope. Le modèle théorique de formation d’image traite la fonction d’étalement du point comme l’unité de base d’une image. En d’autres termes, la fonction d’étalement du point est à l’image ce que la brique est à la maison. Le mieux qu’une image puisse être est un assemblage de fonctions d’étalement du point, et l’augmentation du grossissement ne changera pas ce fait. Comme l’explique un manuel d’optique théorique réputé (Born et Wolf : Principes de l’optique), « il est impossible de faire ressortir des détails qui ne sont pas présents dans l’image primaire en augmentant la puissance de l’oculaire, car chaque élément de l’image primaire est un petit motif de diffraction, et l’image réelle, telle qu’elle est vue par l’oculaire, n’est que l’ensemble des images agrandies de ces motifs ».

À titre d’exemple, considérons une population de perles fluorescentes de sous-résolution prises en sandwich entre une lamelle couvre-objet et une lame de microscope. Une image focalisée de ce spécimen révèle un nuage de points, qui est en fait un disque entouré d’un minuscule ensemble d’anneaux (en fait, un disque d’Airy ; voir la figure 4(a)). Si l’on éloigne légèrement ce spécimen de la mise au point, un ensemble plus grand d’anneaux concentriques apparaît à l’endroit où se trouvait chaque point dans l’image mise au point (figure 4(b)). Lorsqu’une image tridimensionnelle de ce spécimen est recueillie, une fonction d’étalement du point complète est enregistrée pour chaque perle. La fonction d’étalement du point décrit ce qui arrive à chaque source ponctuelle de lumière après son passage dans le système d’imagerie.

Le processus de flou qui vient d’être décrit est mathématiquement modélisé comme une convolution. L’opération de convolution décrit l’application de la fonction d’étalement du point à chaque point du spécimen : la lumière émise par chaque point de l’objet est convoluée avec la fonction d’étalement du point pour produire l’image finale. Malheureusement, cette convolution fait que les points du spécimen deviennent des régions floues dans l’image. La luminosité de chaque point de l’image est liée linéairement par l’opération de convolution à la fluorescence de chaque point du spécimen. Comme la fonction d’étalement du point est tridimensionnelle, le flou de la fonction d’étalement du point est un phénomène intrinsèquement tridimensionnel. L’image provenant de n’importe quel plan focal contient une lumière floue provenant de points situés dans ce plan, mélangée à une lumière floue provenant de points originaires d’autres plans focaux.

La situation peut être résumée par l’idée que l’image est formée par une convolution de l’échantillon avec la fonction d’étalement du point. La déconvolution inverse ce processus et tente de reconstruire le spécimen à partir d’une image floue.

Aberrations dans la fonction d’étalement du point

La fonction d’étalement du point peut être définie soit théoriquement en utilisant un modèle mathématique de la diffraction, soit empiriquement en acquérant une image tridimensionnelle d’une perle fluorescente (voir figure 3). Une fonction d’étalement ponctuel théorique présente généralement une symétrie axiale et radiale. En effet, la fonction d’étalement du point est symétrique au-dessus et au-dessous du plan x-y (symétrie axiale) et en rotation autour de l’axe z (symétrie radiale). Une fonction d’étalement ponctuel empirique peut s’écarter considérablement de la symétrie parfaite (comme le montre la figure 3). Cette déviation, plus communément appelée aberration, est produite par des irrégularités ou des désalignements dans n’importe quel composant du train optique du système d’imagerie, en particulier l’objectif, mais peut également se produire avec d’autres composants tels que les miroirs, les séparateurs de faisceau, les lentilles tubulaires, les filtres, les diaphragmes et les ouvertures. Plus la qualité des composants optiques est élevée et plus l’alignement du microscope est bon, plus la fonction d’étalement du point empirique se rapproche de sa forme symétrique idéale. La microscopie confocale et la microscopie à déconvolution dépendent toutes deux du fait que la fonction d’étalement du point soit aussi proche que possible du cas idéal.

L’aberration la plus courante rencontrée en microscopie optique, bien connue de tout microscopiste expérimenté et professionnel, est l’aberration sphérique. La manifestation de cette aberration est une asymétrie axiale de la forme de la fonction d’étalement du point, avec une augmentation correspondante de la taille, en particulier le long de l’axe z (figure 3). Il en résulte une perte considérable de résolution et d’intensité du signal. Dans la pratique, la source typique d’aberration sphérique est un décalage entre les indices de réfraction du milieu d’immersion de la lentille frontale de l’objectif et du milieu d’enrobage dans lequel baigne l’échantillon. Il convient d’insister sur l’importance de minimiser cette aberration. Bien que la déconvolution puisse partiellement restaurer la résolution perdue, aucune quantité de traitement d’image ne peut restaurer le signal perdu.

.