Fonction de Green

Généralement parlant, une fonction de Green est un noyau intégral qui peut être utilisé pour résoudre des équations différentielles d’un grand nombre de familles, y compris des exemples plus simples comme les équations différentielles ordinaires avec des conditions de valeurs initiales ou limites, ainsi que des exemples plus difficiles comme les équations différentielles partielles inhomogènes (EDP) avec des conditions limites. Importantes pour un certain nombre de raisons, les fonctions de Green permettent des interprétations visuelles des actions associées à une source de force ou à une charge concentrée en un point (Qin 2014), ce qui les rend particulièrement utiles dans les domaines des mathématiques appliquées. En particulier, les méthodes de la fonction de Green sont largement utilisées dans, par ex, la physique et l’ingénierie.

Plus précisément, étant donné un opérateur différentiel linéaire agissant sur la collection de distributions sur un sous-ensemble d’un certain espace euclidien , une fonction de Green au point correspondant à est toute solution de

(1)

où désigne la fonction delta. La motivation pour définir une telle fonction est très répandue, mais en multipliant l’identité ci-dessus par une fonction et en intégrant par rapport à on obtient

(2)

Le côté droit se réduit simplement à en raison des propriétés de la fonction delta, et parce que est un opérateur linéaire n’agissant que sur et non sur , le côté gauche peut être réécrit comme

(3)

Cette réduction est particulièrement utile pour résoudre dans des équations différentielles de la forme

(4)

où l’arithmétique ci-dessus confirme que

(5)

et d’où il résulte que a la forme intégrale spécifique

(6)

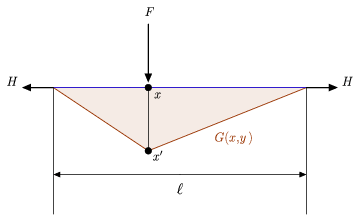
La figure ci-dessus illustre à la fois l’interprétation physique intuitive d’une fonction de Green ainsi qu’une équation différentielle associée relativement simple avec laquelle comparer la définition ci-dessus (Hartmann 2013). En particulier, elle montre une corde tendue de longueur suspendue entre deux murs, maintenue en place par une force horizontale identique appliquée sur chacune de ses extrémités, et une charge latérale placée en un point intérieur sur la corde. Soit le point correspondant à sur la corde déviée, on suppose que la force descendante est constante, disons , et on désigne par la déviation de la corde. A ce système physique correspond l’équation différentielle

(7)

pour avec , un système dont la simplicité permet à la fois d’écrire explicitement sa solution et sa fonction de Green :

(8)

et

(9)

respectivement. Comme démontré dans la figure ci-dessus, la corde déplacée a le format linéaire par morceaux donné par ci-dessus, confirmant ainsi l’affirmation selon laquelle la fonction de Green associée à ce système représente l’action de la corde horizontale correspondant à l’application d’une force .

Une fonction de Green prenant une paire d’arguments est parfois appelée fonction de Green à deux points. Ceci par opposition aux fonctions de Green à plusieurs points qui ont une importance particulière dans le domaine de la théorie des corps multiples.

Comme exemple élémentaire d’une fonction à deux points telle que définie ci-dessus, considérons le problème de la détermination du potentiel généré par une distribution de charge dont la densité de charge est , où les applications de l’équation de Poisson et de la loi de Coulomb au potentiel à produit par chaque élément de charge donnent une solution

(10)

qui tient, sous certaines conditions, sur la région où . Comme le côté droit peut être considéré comme un opérateur intégral convertissant en , on peut réécrire cette solution en termes d’une fonction de Green ayant la forme

(11)

où la solution peut être réécrite :

(12)

(Arfken 2012).

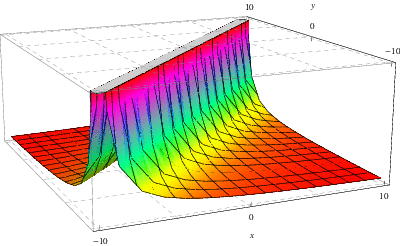
La figure ci-dessus montre la fonction de Green associée à la solution de l’équation – discutée ci-dessus où ici, et , respectivement , est tracée sur l’axe -, respectivement -.

Une liste assez complète des fonctions de Green correspondant à diverses équations différentielles est maintenue en ligne par Kevin Cole (Cole 2000).

En raison de la multitude de littérature écrite sur les fonctions de Green, plusieurs notations et définitions différentes peuvent émerger, dont certaines sont topiquement différentes de celles ci-dessus, mais qui en général n’affectent pas les propriétés importantes des résultats. Comme l’illustre l’exemple ci-dessus, par exemple, certains auteurs préfèrent désigner les variables et en termes de vecteurs et pour souligner le fait qu’elles sont des éléments de pour un certain qui peut être plus grand que 1 (Arfken 1985). Il est également relativement courant de voir la définition avec un signe négatif de sorte que est définie comme étant la fonction pour laquelle

(13)

mais du fait que cette considération purement physique n’a aucun effet sur les mathématiques sous-jacentes, ce point de vue est généralement négligé. Plusieurs autres notations sont également connues pour une fonction de Green, dont certaines incluent l’utilisation d’une minuscule à la place de (Stakgold 1979) ainsi que l’inclusion d’un trait vertical au lieu d’une virgule, par ex, (Duffy 2001).

Dans d’autres cas, la littérature présente des définitions qui sont intimement liées aux contextes dans lesquels elles sont présentées. Par exemple, certains auteurs définissent les fonctions de Green comme des fonctions qui satisfont un certain ensemble de conditions, par exemple,l’existence sur un type spécial de domaine, l’association avec un opérateur différentiel très particulier , ou la satisfaction d’un ensemble précis de conditions aux limites. L’un des exemples les plus courants de ce type se trouve dans les notes de, par ex, Speck, où une fonction de Green est définie pour satisfaire pour les points et pour tous les points situés dans la limite de (Speck 2011). Cette définition particulière présente un noyau intégral correspondant à la solution d’une équation de Poisson généralisée et serait donc confrontée à des limitations évidentes lors de son adaptation à un cadre plus général. D’un autre côté, de tels exemples ne sont pas sans avantages. Dans le cas de l’exemple de Poisson généralisé ci-dessus, par exemple, chacune de ces fonctions de Green peut être divisée de sorte que

(14)

où et pour le Laplacien régulier (Hartman 2013). Dans de telles situations, est connu comme la solution fondamentale de l’équation différentielle sous-jacente et est connu comme sa solution régulière ; à ce titre, et sont parfois appelés les parties fondamentale et régulière de , respectivement.

Plusieurs propriétés fondamentales d’une fonction de Green générale découlent immédiatement (ou presque) de sa définition et se reportent sur toutes les instances particulières. Par exemple, si le noyau de l’opérateur est non trivial, alors il peut y avoir plusieurs fonctions de Green associées à un seul opérateur ; par conséquent, il faut faire preuve de prudence lorsqu’on se réfère à « la » fonction de Green. Les fonctions de Green satisfont une symétrie adjointe dans leurs deux arguments de sorte que

(15)

où ici, est défini comme étant la solution de l’équation

(16)

Ici, est l’adjoint de . Un corollaire immédiat de ce fait est que pour les opérateurs auto-adjoints , est symétrique:

(17)

Cette identité est souvent appelée principe de réciprocité et dit, en termes physiques, que la réponse à causée par une source unitaire à est la même que la réponse à due à une force unitaire à (Stakgold 1979).

La propriété essentielle de toute fonction de Green est qu’elle fournit un moyen de décrire la réponse d’une solution d’équation différentielle arbitraire à un certain type de terme source en présence d’un certain nombre de conditions aux limites (Arfken et al. 2012). Certains auteurs considèrent qu’une fonction de Green joue un rôle à peu près analogue dans la théorie des équations aux dérivées partielles à celui des séries de Fourier dans la solution des équations différentielles ordinaires (Mikula et Kos 2006).

Pour des scénarios plus abstraits, il existe un certain nombre de concepts qui servent d’analogues spécifiques au contexte à la notion de fonction de Green. Par exemple, en analyse fonctionnelle, il est souvent utile de considérer une fonction de Green dite généralisée qui possède de nombreuses propriétés analogues lorsqu’elle est intégrée abstraitement par rapport aux fonctionnelles plutôt qu’aux fonctions. En effet, de telles généralisations ont donné lieu à une branche entièrement analogue de l’analyse théorique des EDP et font elles-mêmes l’objet d’un grand nombre de recherches.

.