Filtrage bilinéaire & interpolation bilinéaire

Regardez l’image ci-dessous. Pouvez-vous calculer les valeurs aux points A,B et C ?

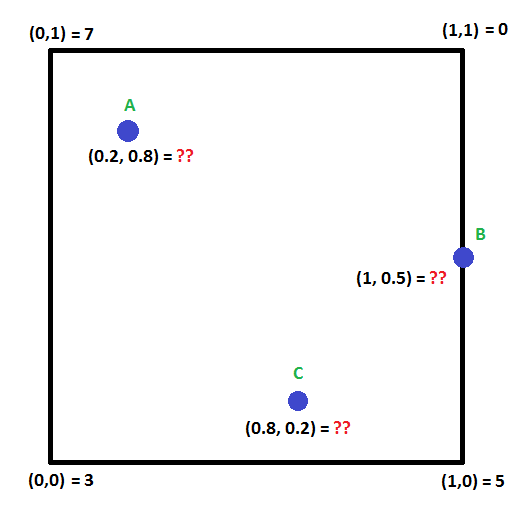
Il existe une technique pour faire cela appelée interpolation bilinéaire qui étend l’idée d’interpolation linéaire à deux dimensions.

Pour calculer l’interpolation bilinéaire, il suffit de faire une interpolation linéaire sur un axe, puis sur l’autre.

Voyez ces exemples :

Point A
Le point A a une coordonnée de (0,2,0,8). Commençons par l’axe des X.

D’abord, nous allons faire une interpolation à travers le haut du carré sur l’axe des X. Cela signifie que nous devons aller 0,2 (20%) du chemin de 7 à 0. Ce 0,2 est notre coordonnée d’axe x. Pour calculer cela, nous faisons ceci :
7 + (0-7) * 0,2 = 5,6

Puis, nous allons faire l’interpolation à travers le bas du carré sur l’axe X. Donc, de manière similaire à ce qui précède, nous allons faire 0,2 (20%) du chemin de 3 à 5. Pour calculer cela, nous faisons ceci :
3 + (5-3) * 0,2 = 3,4

Maintenant que nous avons interpolé à travers notre axe X, nous devons interpoler à travers notre axe Y. Nous allons maintenant parcourir 0,8 (80 %) du chemin entre la valeur inférieure (la valeur de Y = 0) et la valeur supérieure (la valeur de Y = 1). La valeur inférieure est l’interpolation inférieure que nous avons faite (3,4) et la valeur supérieure est l’interpolation supérieure que nous avons faite (5,6).

Donc, nous devons faire 0,8 (80%) du chemin de 3,4 à 5,6. Pour calculer cela, nous faisons ceci :
3,4 + (5,6 – 3,4) * 0,8 = 5,16

Donc, la valeur au point A est 5,16. L’image ci-dessous devrait aider à expliquer visuellement le processus par lequel nous sommes passés.

Point B

Le point B a des coordonnées de (1,0,0,5).

Recommençons par l’interpolation de l’axe X (bien que vous pourriez facilement commencer par l’axe Y si vous le vouliez ! Vous obtiendriez le même résultat).

En faisant l’interpolation de l’axe X à travers le haut, nous avons besoin d’aller 1,0 (100%) du chemin de 7 à 0. Je suis sûr que vous pouvez deviner la réponse, mais voici le calcul :
7 + (0-7) * 1,0 = 0

De même, faisons l’interpolation de l’axe X à travers le bas. Nous avons besoin d’aller 1,0 (100%) du chemin de 3 à 5.
3 + (5-3) * 1,0 = 5

Vient ensuite l’interpolation de l’axe Y. Nous devons faire 0,5 (50%) du chemin de 5 à 0.
5 + (0-5) * 0,5 = 2,5

Voilà, la valeur au point B est 2,5. Cela devrait être logique aussi en regardant le diagramme. C’est essentiellement une interpolation linéaire 1d entre 5 et 0, et c’est à mi-chemin entre les deux, donc intuitivement, la réponse 2,5 devrait être logique.

Point C

Le point C a une coordonnée de (0,8,0,2).

Une fois de plus, faisons l’interpolation de l’axe X à travers le haut de la boîte. Nous devons aller 0,8 (80%) du chemin de 7 à 0.
7 + (0-7) * 0,8 = 1,4

Puis, nous devons faire l’interpolation de l’axe x à travers le bas de la boîte. Nous devons aller 0,8 (80%) du chemin de 3 à 5.
3 + (5-3) * 0,8 = 4,6

En dernier lieu, l’interpolation de l’axe y. Nous devons passer de 0,2 (20%) de 4,6 à 1,4.
4,6 + (1,4-4,6) * 0,2 = 3,96

La valeur du point C est 3.96

Filtrage bilinéaire

Bien que l’interpolation bilinéaire soit utile si vous avez une grille de données dans laquelle vous voulez interpoler des valeurs (comme un champ de hauteur qui représente le terrain ? !), là où cela brille vraiment dans le développement de jeux, c’est dans le filtrage de texture bilinéaire.

Basiquement, lorsque vous avez une coordonnée de texture qui n’est pas parfaitement alignée avec le centre d’un pixel dans la texture (parce qu’il y a un reste), il utilise la partie fractionnaire de la coordonnée dans ce pixel pour faire une interpolation bilinéaire entre les 4 pixels impliqués pour arriver à la couleur finale du pixel. Il effectue une interpolation bilinéaire sur chacun des canaux : Rouge, Vert, Bleu et Alpha.

Le résultat final est plutôt bon ! Regardez l’image ci-dessous pour le voir en action sur une texture sur laquelle nous avons fait un zoom trop important. Le côté gauche utilise le filtrage bilinéaire, tandis que le côté droit ne le fait pas, et vous montre juste le pixel le plus proche.

En conséquence, le filtrage de texture bilinéaire doit faire 4 lectures de pixels pour pouvoir interpoler entre eux, au lieu d’une seule lecture de pixel comme lors de l’échantillonnage du pixel le plus proche. Plus de lectures de pixels = plus de frais généraux, et pas aussi bon marché (en termes de calcul) à utiliser.

Liens

Pour certaines personnes qui lisent ceci, cette info est assez basique et vous pourriez vous demander pourquoi j’ai pris la peine d’écrire à ce sujet. Regardez le prochain post pour quelque chose d’assez bizarre concernant le filtrage bilinéaire. Ceci était nécessaire comme un tremplin vers la prochaine chose que je veux vous montrer les gars 😛

Wikipedia : Interpolation linéaire

Wikipedia : Interpolation bilinéaire

Wikipedia : Filtrage bilinéaire

Le côté obscur du filtrage bilinéaire

Consultez ces liens pour obtenir des informations plus approfondies sur certains défauts (et certaines solutions de contournement) de l’échantillonnage bilinéaire basé sur le matériel :
iq : interpolation matérielle
iq : interpolation de texture améliorée

.