9.5 – Identification des points de données influents

Dans cette section, nous apprenons les deux mesures suivantes pour identifier les points de données influents :

• Différence dans les ajustements (DFFITS)
• Distances de Cook

L’idée de base derrière chacune de ces mesures est la même, à savoir supprimer les observations une par une, en réajustant chaque fois le modèle de régression sur les n-1 observations restantes. Ensuite, nous comparons les résultats utilisant l’ensemble des n observations aux résultats avec la ième observation supprimée pour voir l’influence de l’observation sur l’analyse. Analysé ainsi, nous sommes en mesure d’évaluer l’impact potentiel de chaque point de données sur l’analyse de régression.

Différence dans les ajustements (DFFITS)

La différence dans les ajustements pour l’observation i, notée DFFITSi, est définie comme:

\

Comme vous pouvez le voir, le numérateur mesure la différence dans les réponses prédites obtenues lorsque le ième point de données est inclus et exclu de l’analyse. Le dénominateur est l’écart type estimé de la différence dans les réponses prédites. Par conséquent, la différence d’ajustement quantifie le nombre d’écarts types que la valeur ajustée change lorsque le ie point de données est omis.

Une observation est jugée influente si la valeur absolue de sa valeur DFFITS est supérieure à :

où, comme toujours, n = le nombre d’observations et k = le nombre de termes prédicteurs (c’est-à-dire le nombre de paramètres de régression excluant l’intercept). Il est important de garder à l’esprit qu’il ne s’agit pas d’une règle absolue, mais plutôt d’une ligne directrice seulement ! Il n’est pas difficile de trouver différents auteurs utilisant une ligne directrice légèrement différente. Par conséquent, je préfère souvent une ligne directrice beaucoup plus subjective, telle qu’un point de données est considéré comme influent si la valeur absolue de sa valeur DFFITS ressort comme un pouce endormi par rapport aux autres valeurs DFFITS. Bien sûr, il s’agit d’un jugement qualitatif, peut-être comme il se doit, puisque les valeurs aberrantes sont par nature des quantités subjectives.

Exemple #2 (encore). Vérifions la différence de mesure des ajustements pour cet ensemble de données (influence2.txt):

En régressant y sur x et en demandant la différence d’ajustement, nous obtenons la sortie logicielle suivante :

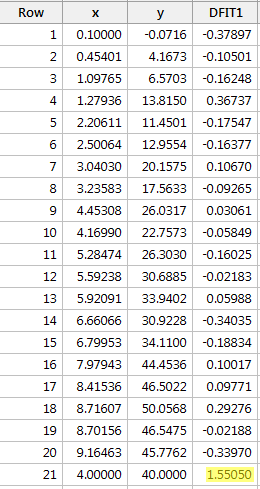
En utilisant la ligne directrice objective définie ci-dessus, nous considérons qu’un point de données est influent si la valeur absolue de sa valeur DFFITS est supérieure à :

\

Un seul point de données – le rouge – a une valeur DFFITS dont la valeur absolue (1.55050) est supérieure à 0,82. Par conséquent, sur la base de cette ligne directrice, nous considérerions le point de données rouge comme influent.

Exemple n°3 (à nouveau). Vérifions la différence de mesure des ajustements pour cet ensemble de données (influence3.txt):

Régresser y sur x et demander la différence d’ajustement, nous obtenons la sortie logicielle suivante :

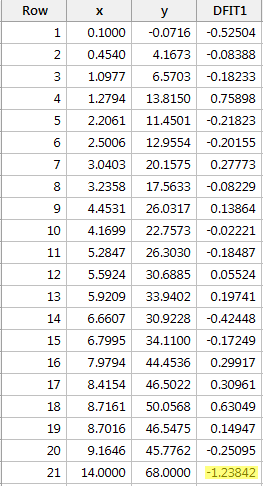
En utilisant la ligne directrice objective définie ci-dessus, nous considérons qu’un point de données est influent si la valeur absolue de sa valeur DFFITS est supérieure à :

Un seul point de données – le rouge – a une valeur DFFITS dont la valeur absolue (1.23841) est supérieure à 0,82. Par conséquent, sur la base de cette directive, nous considérerions le point de données rouge comme influent.

Lorsque nous avons étudié cet ensemble de données au début de cette leçon, nous avons décidé que le point de données rouge n’affectait pas tant que cela l’analyse de régression. Pourtant, ici, la différence dans la mesure des ajustements suggère qu’il est effectivement influent. Que se passe-t-il ici ? Il s’agit de reconnaître que toutes les mesures de cette leçon ne sont que des outils qui signalent les points de données potentiellement influents pour l’analyste de données. En fin de compte, l’analyste doit analyser l’ensemble des données deux fois – une fois avec et une fois sans les points de données marqués. Si les points de données modifient de manière significative le résultat de l’analyse de régression, alors le chercheur devrait rapporter les résultats des deux analyses.

Par hasard, dans cet exemple ici, si nous utilisons la ligne directrice plus subjective de savoir si la valeur absolue de la valeur DFFITS ressort comme un pouce endolori, nous sommes susceptibles de ne pas juger le point de données rouge comme étant influent. Après tout, la prochaine plus grande valeur de DFFITS (en valeur absolue) est 0,75898. Cette valeur de DFFITS n’est pas si différente de la valeur de DFFITS de notre point de données « influent ».

Exemple n°4 (encore). Vérifions la mesure de la différence des ajustements pour cet ensemble de données (influence4.txt):

En régressant y sur x et en demandant la différence d’ajustement, nous obtenons la sortie logicielle suivante :

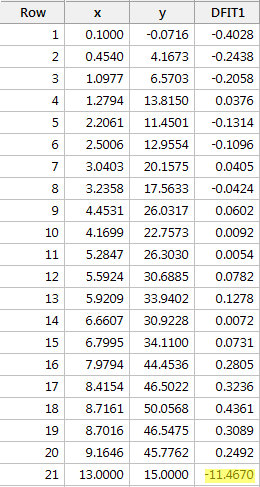
En utilisant la ligne directrice objective définie ci-dessus, nous considérons à nouveau qu’un point de données est influent si la valeur absolue de sa valeur DFFITS est supérieure à :

\

Que pensez-vous ? Est-ce que l’une des valeurs de DFFITS ressort comme un pouce endormi ? Errr – la valeur DFFITS du point de données rouge (-11.4670 ) est certainement d’une magnitude différente de toutes les autres. Dans ce cas, il devrait y avoir peu de doute que le point de données rouge est influent!

Distance de Cook

Pour faire un saut ici, la mesure de distance de Cook, désignée par Di, est définie comme:

\.\]

Cela semble un peu désordonné, mais la principale chose à reconnaître est que la Di de Cook dépend à la fois du résidu, ei (dans le premier terme), et de l’effet de levier, hii (dans le second terme). Autrement dit, la valeur x et la valeur y du point de données jouent toutes deux un rôle dans le calcul de la distance de Cook.

En bref :

• Di résume directement de combien toutes les valeurs ajustées changent lorsque la ième observation est supprimée.
• Un point de données ayant un grand Di indique que le point de données influence fortement les valeurs ajustées.

Etudions ce que signifie exactement cette première affirmation dans le contexte de certains de nos exemples.

Exemple #1 (encore). Vous vous souvenez peut-être que le tracé de ces données (influence1.txt) suggère qu’il n’y a pas de valeurs aberrantes ni de points de données influents pour cet exemple :

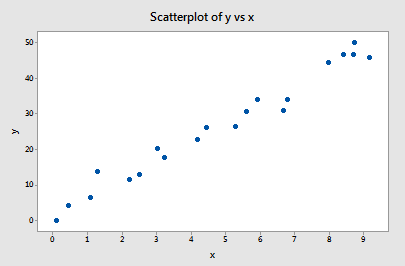
Si nous régressons y sur x en utilisant tous les n = 20 points de données, nous déterminons que le coefficient d’interception estimé b0 = 1,732 et le coefficient de pente estimé b1 = 5,117. Si nous supprimons le premier point de données de l’ensemble de données et que nous régressons y sur x en utilisant les n = 19 points de données restants, nous déterminons que le coefficient d’interception estimé b0 = 1,732 et le coefficient de pente estimé b1 = 5,1169. Comme nous l’espérions et le prévoyions, les estimations ne changent pas beaucoup lorsque l’on supprime un point de données. En poursuivant ce processus de suppression de chaque point de données un par un, et en traçant les pentes estimées résultantes (b1) en fonction des intercepts estimés (b0), nous obtenons :

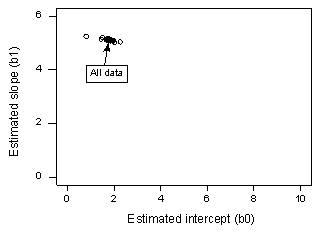
Le point noir plein représente les coefficients estimés basés sur l’ensemble des n = 20 points de données. Les cercles ouverts représentent chacun des coefficients estimés obtenus en supprimant chaque point de données un par un. Comme vous pouvez le constater, les coefficients estimés sont tous regroupés, quel que soit le point de données supprimé, le cas échéant. Cela suggère qu’aucun point de données n’influence indûment la fonction de régression estimée ou, à son tour, les valeurs ajustées. Dans ce cas, nous nous attendrions à ce que toutes les mesures de distance de Cook, Di, soient petites.

Exemple n°4 (encore). Vous vous souvenez peut-être que le tracé de ces données (influence4.txt) suggère qu’un point de données est influent et constitue une valeur aberrante pour cet exemple :

Si nous régressons y sur x en utilisant tous les points de données n = 21, nous déterminons que le coefficient d’interception estimé b0 = 8,51 et le coefficient de pente estimé b1 = 3,32. Si nous supprimons le point de données rouge de l’ensemble de données et que nous régressons y sur x en utilisant les n = 20 points de données restants, nous déterminons que le coefficient d’interception estimé b0 = 1,732 et le coefficient de pente estimé b1 = 5,1169. Les estimations changent considérablement lorsqu’on supprime un seul point de données. En continuant ce processus de suppression de chaque point de données un par un, et en traçant les pentes estimées résultantes (b1) en fonction des intercepts estimés (b0), nous obtenons :

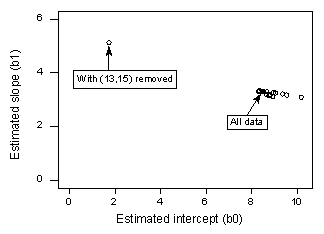
De nouveau, le point noir plein représente les coefficients estimés basés sur l’ensemble des n = 21 points de données. Les cercles ouverts représentent chacun des coefficients estimés obtenus en supprimant chaque point de données un par un. Comme vous pouvez le constater, à l’exception du point de données rouge (x = 13, y = 15), les coefficients estimés sont tous regroupés, quel que soit le point de données supprimé, le cas échéant. Cela suggère que le point de données rouge est le seul point de données qui influence indûment la fonction de régression estimée et, à son tour, les valeurs ajustées. Dans ce cas, nous nous attendrions à ce que la mesure de distance de Cook, Di, pour le point de données rouge soit grande et que les mesures de distance de Cook, Di, pour les autres points de données soient petites.

Utilisation des mesures de distance de Cook. La beauté des exemples ci-dessus est la possibilité de voir ce qui se passe avec des graphiques simples. Malheureusement, nous ne pouvons pas compter sur des tracés simples dans le cas de la régression multiple. Au lieu de cela, nous devons nous appuyer sur des lignes directrices pour décider quand une mesure de distance de Cook est suffisamment grande pour justifier le traitement d’un point de données comme influent.

Voici les lignes directrices couramment utilisées :

• Si Di est supérieur à 0,5, alors le ième point de données mérite une enquête plus approfondie car il peut être influent.
• Si Di est supérieur à 1, alors le ie point de données est tout à fait susceptible d’être influent.
• Ou, si Di ressort comme un pouce endormi des autres valeurs Di, il est presque certainement influent.

Exemple n°2 (encore). Vérifions la mesure de la distance de Cook pour cet ensemble de données (influence2.txt):

En régressant y sur x et en demandant les mesures de distance de Cook, nous obtenons la sortie logicielle suivante:

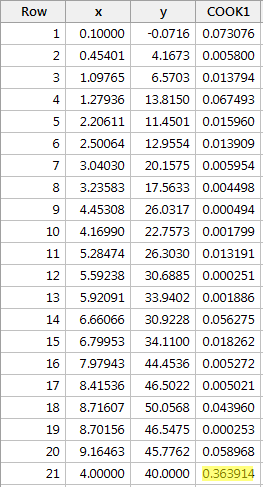
La mesure de distance de Cook pour le point de données rouge (0,363914) se démarque un peu par rapport aux autres mesures de distance de Cook. Pourtant, la mesure de distance de Cook pour le point de données rouge est inférieure à 0,5. Par conséquent, sur la base de la mesure de distance de Cook, nous ne classerions pas le point de données rouge comme étant influent.

Exemple n°3 (encore). Vérifions la mesure de distance de Cook pour cet ensemble de données (influence3.txt):

En régressant y sur x et en demandant les mesures de distance de Cook, nous obtenons la sortie logicielle suivante:

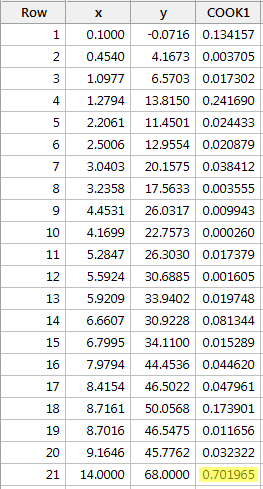
La mesure de distance de Cook pour le point de données rouge (0,701965) se démarque un peu par rapport aux autres mesures de distance de Cook. Pourtant, la mesure de distance de Cook pour le point de données rouge est plus grande que 0,5 mais inférieure à 1. Par conséquent, sur la base de la mesure de distance de Cook, nous pourrions peut-être enquêter davantage mais pas nécessairement classer le point de données rouge comme étant influent.

Exemple #4 (encore). Vérifions la mesure de distance de Cook pour cet ensemble de données (influence4.txt):

En régressant y sur x et en demandant les mesures de distance de Cook, nous obtenons la sortie logicielle suivante:

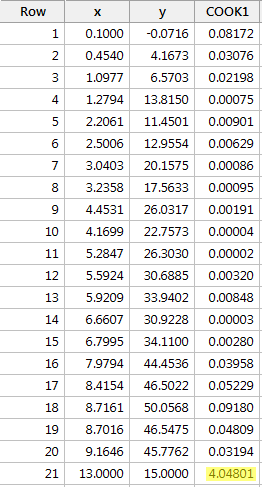
Dans ce cas, la mesure de distance de Cook pour le point de données rouge (4.04801) se démarque considérablement par rapport aux autres mesures de distance de Cook. En outre, la mesure de distance de Cook pour le point de données rouge est supérieure à 1. Par conséquent, sur la base de la mesure de distance de Cook – et sans surprise – nous classerions le point de données rouge comme étant influent.

Une autre méthode d’interprétation de la distance de Cook qui est parfois utilisée consiste à relier la mesure à la distribution F(k+1, n-k-1) et à trouver la valeur du percentile correspondant. Si ce percentile est inférieur à environ 10 ou 20 pour cent, alors le cas a peu d’influence apparente sur les valeurs ajustées. En revanche, s’il est proche de 50 % ou même supérieur, le cas a une influence majeure. (Tout ce qui se situe « entre les deux » est plus ambigu.)