8.3 : Gaz et pression

La phase gazeuse est unique parmi les trois états de la matière en ce qu’il existe certains modèles simples que nous pouvons utiliser pour prédire le comportement physique de tous les gaz – indépendamment de leur identité. Nous ne pouvons pas faire cela pour les états solide et liquide. En fait, le développement de cette compréhension du comportement des gaz représente le point de division historique entre l’alchimie et la chimie moderne. Les premières avancées dans la compréhension du comportement des gaz ont été réalisées au milieu des années 1600 par Robert Boyle, un scientifique anglais qui a fondé la Royal Society (l’une des plus anciennes organisations scientifiques du monde).

Comment se fait-il que nous puissions modéliser tous les gaz indépendamment de leur identité chimique ? La réponse se trouve dans un groupe d’énoncés appelés la théorie cinétique des gaz :

• Les gaz sont composés de minuscules particules qui sont séparées par de grandes distances.
• Les particules de gaz sont constamment en mouvement, subissant des collisions avec d’autres particules de gaz et les parois de leur récipient.
• La vitesse des particules de gaz est liée à la température d’un gaz.
• Les particules de gaz ne subissent aucune force d’attraction ou de répulsion entre elles.

Avez-vous remarqué qu’aucune de ces affirmations ne se rapporte à l’identité du gaz ? Cela signifie que tous les gaz devraient se comporter de manière similaire. Un gaz qui suit parfaitement ces déclarations est appelé un gaz idéal. La plupart des gaz présentent de légères déviations par rapport à ces déclarations et sont appelés gaz réels. Cependant, l’existence de gaz réels ne diminue pas l’importance de la théorie cinétique des gaz.

L’une des déclarations de la théorie cinétique mentionne les collisions. Comme les particules de gaz sont constamment en mouvement, elles entrent aussi constamment en collision les unes avec les autres et avec les parois de leur récipient. Des forces sont impliquées lorsque les particules de gaz rebondissent sur les parois du récipient (figure \(\PageIndex{1}\)). La force générée par les particules de gaz divisée par la surface des parois du récipient donne la pression. La pression est une propriété que nous pouvons mesurer pour un gaz, mais nous ne considérons généralement pas la pression pour les solides ou les liquides.

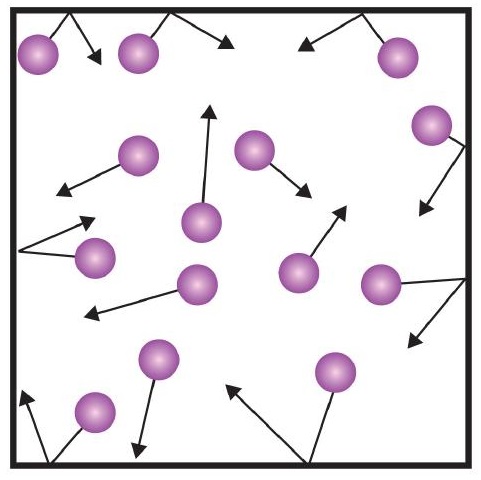
L’unité de base de la pression est le newton par mètre carré (N/m2). Cette unité combinée est redéfinie comme un pascal (Pa). Un pascal n’est pas une très grande quantité de pression. Une unité de pression plus utile est le bar, qui correspond à 100 000 Pa (1 bar = 100 000 Pa). Les autres unités de pression courantes sont l’atmosphère (atm), définie à l’origine comme la pression moyenne de l’atmosphère terrestre au niveau de la mer, et le mmHg (millimètres de mercure), qui est la pression générée par une colonne de mercure de 1 mm de haut. L’unité millimètre de mercure est également appelée torr, du nom du scientifique italien Evangelista Torricelli, qui a inventé le baromètre au milieu des années 1600. Une définition plus précise de l’atmosphère, en termes de torr, est qu’il y a exactement 760 torr dans 1 atm. Un bar est égal à 1,01325 atm. Compte tenu de toutes les relations entre ces unités de pression, la capacité de convertir une unité de pression en une autre est une compétence utile.

La théorie cinétique stipule également qu’il n’y a aucune interaction entre les particules de gaz individuelles. Bien que nous sachions qu’il existe, en fait, des interactions intermoléculaires dans les gaz réels, la théorie cinétique suppose que les particules de gaz sont si éloignées les unes des autres que les particules individuelles ne se « sentent » pas. Ainsi, nous pouvons traiter les particules de gaz comme de minuscules morceaux de matière dont l’identité n’est pas importante pour certaines propriétés physiques.

.