Échantillonnage de Gibbs

Comme les autres méthodes MCMC, l’échantillonneur de Gibbs construit une chaîne de Markov dont les valeurs convergent vers une distribution cible. L’échantillonneur de Gibbs est en fait un cas spécifique de l’algorithme de Metropolis-Hastings dans lequel les propositions sont toujours acceptées.

Pour développer, supposons que vous vouliez échantillonner une distribution de probabilité multivariée.

Note : Une distribution de probabilité multivariée est une fonction de plusieurs variables (ex. distribution normale à 2 dimensions).

Nous ne savons pas comment échantillonner directement cette dernière. Cependant, en raison d’une certaine commodité mathématique ou peut-être simplement de la chance, il se trouve que nous connaissons les probabilités conditionnelles.

C’est là que l’échantillonnage de Gibbs intervient. L’échantillonnage de Gibbs est applicable lorsque la distribution conjointe n’est pas connue explicitement ou qu’il est difficile d’échantillonner directement, mais que la distribution conditionnelle de chaque variable est connue et plus facile à échantillonner.

Nous commençons par sélectionner une valeur initiale pour les variables aléatoires X &Y. Ensuite, nous échantillonnons à partir de la distribution de probabilité conditionnelle de X étant donné Y = Y⁰ notée p(X|Y⁰). À l’étape suivante, nous échantillonnons une nouvelle valeur de Y conditionnelle à X¹, que nous venons de calculer. Nous répétons la procédure pour n – 1 itérations supplémentaires, en alternant entre le tirage d’un nouvel échantillon de la distribution de probabilité conditionnelle de X et de la distribution de probabilité conditionnelle de Y, étant donné la valeur actuelle de l’autre variable aléatoire.

Regardons un exemple. Supposons que nous ayons les distributions de probabilité postérieure et conditionnelle suivantes .

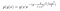
où g(y) contient les termes qui n’incluent pas x, et g(x) contient ceux qui ne dépendent pas de y.

Nous ne connaissons pas la valeur de C (constante de normalisation). Cependant, nous connaissons les distributions de probabilité conditionnelles. Par conséquent, nous pouvons utiliser l’échantillonnage de Gibbs pour approximer la distribution postérieure.

Note : Les probabilités conditionnelles sont en fait des distributions normales, et peuvent être réécrites comme suit.

Ayant donné les équations précédentes, nous procédons à l’implémentation de l’algorithme d’échantillonnage de Gibbs en Python. Pour commencer, nous importons les bibliothèques suivantes.

import numpy as np
import scipy as sp
import matplotlib.pyplot as plt
import pandas as pd
import seaborn as sns
sns.set()

Nous définissons la fonction pour la distribution postérieure (supposons C=1).

f = lambda x, y: np.exp(-(x*x*y*y+x*x+y*y-8*x-8*y)/2.)

Puis, nous traçons la distribution de probabilité.

xx = np.linspace(-1, 8, 100)
yy = np.linspace(-1, 8, 100)
xg,yg = np.meshgrid(xx, yy)
z = f(xg.ravel(), yg.ravel())
z2 = z.reshape(xg.shape)
plt.contourf(xg, yg, z2, cmap='BrBG')

Maintenant, nous allons tenter d’estimer la distribution de probabilité en utilisant l’échantillonnage de Gibbs. Comme nous l’avons mentionné précédemment, les probabilités conditionnelles sont des distributions normales. Par conséquent, nous pouvons les exprimer en termes de mu et sigma.

Dans le bloc de code suivant, nous définissons des fonctions pour mu et sigma, nous initialisons nos variables aléatoires X & Y, et nous définissons N (le nombre d’itérations).

N = 50000
x = np.zeros(N+1)
y = np.zeros(N+1)
x = 1.
y = 6.
sig = lambda z, i: np.sqrt(1./(1.+z*z))
mu = lambda z, i: 4./(1.+z*z)

Nous passons par l’algorithme d’échantillonnage de Gibbs.

for i in range(1, N, 2):
sig_x = sig(y, i-1)
mu_x = mu(y, i-1)
x = np.random.normal(mu_x, sig_x)
y = y
sig_y = sig(x, i)
mu_y = mu(x, i)
y = np.random.normal(mu_y, sig_y)
x = x

Enfin, nous traçons les résultats.

plt.hist(x, bins=50);
plt.hist(y, bins=50);

plt.contourf(xg, yg, z2, alpha=0.8, cmap='BrBG')
plt.plot(x,y, '.', alpha=0.1)
plt.plot(x,y, c='r', alpha=0.3, lw=1)

Comme on peut le voir, la distribution de probabilité obtenue par l’algorithme d’échantillonnage de Gibbs fait un bon travail d’approximation de la distribution cible.

Conclusion

L’échantillonnage de Gibbs est une méthode de Monte Carlo par chaîne de Markov qui tire itérativement une instance de la distribution de chaque variable, conditionnellement aux valeurs actuelles des autres variables afin d’estimer des distributions conjointes complexes. Contrairement à l’algorithme de Metropolis-Hastings, on accepte toujours la proposition. Ainsi, l’échantillonnage de Gibbs peut être beaucoup plus efficace.