Vapaiden taiteiden matematiikka

Visuaalisen itsesimilaarisuuden lisäksi fraktaaleilla on muitakin mielenkiintoisia ominaisuuksia. Huomaa esimerkiksi, että Sierpinski-tiivisteen iteraation jokainen askel poistaa neljänneksen jäljellä olevasta pinta-alasta. Jos tätä prosessia jatketaan loputtomiin, päädymme siihen, että poistamme käytännössä koko alueen, eli aloitimme kaksiulotteisesta alueesta, ja jotenkin päädymme johonkin sitä pienempään, mutta näennäisesti enemmän kuin vain yksiulotteiseen viivaan.

Tämän ajatuksen tutkimiseksi meidän on keskusteltava ulottuvuudesta. Jokin viivan kaltainen on 1-ulotteinen; sillä on vain pituus. Mikä tahansa käyrä on 1-ulotteinen. Laatikoiden ja ympyröiden kaltaiset asiat ovat 2-ulotteisia, koska niillä on pituus ja leveys, jotka kuvaavat aluetta. Laatikoiden ja sylinterien kaltaisilla esineillä on pituus, leveys ja korkeus, jotka kuvaavat tilavuutta, ja ne ovat 3-ulotteisia.

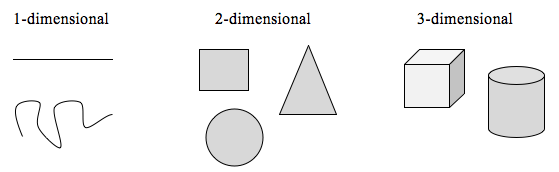
Objektien skaalaamiseen sovelletaan tiettyjä sääntöjä, jotka liittyvät niiden ulottuvuuteen.

Jos minulla olisi viiva, jonka pituus on 1, ja haluaisin skaalata sen pituuden 2:lla, tarvitsisin kaksi kopiota alkuperäisestä viivasta. Jos minulla olisi viiva, jonka pituus on 1, ja haluaisin skaalata sen pituuden kolmella, tarvitsisin kolme kopiota alkuperäisestä.

Jos minulla olisi suorakulmio, jonka pituus on 2 ja korkeus 1, ja haluaisin skaalata sen pituuden ja leveyden kahdella, tarvitsisin neljä kopiota alkuperäisestä suorakulmiosta. Jos haluaisin skaalata sen pituuden ja leveyden 3:lla, tarvitsisin yhdeksän kopiota alkuperäisestä suorakulmiosta.

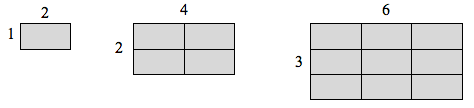
Jos minulla olisi kuutiomainen laatikko, jonka sivut ovat pituudeltaan 1, ja haluaisin skaalata sen pituuden ja leveyden 2:lla, tarvitsisin kahdeksan kopiota alkuperäisestä kuutiosta. Jos haluaisin skaalata sen pituuden ja leveyden 3:lla, tarvitsisin 27 kopiota alkuperäisestä kuutiosta.

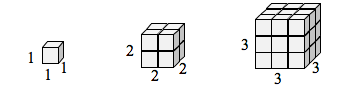
Huomaa, että 1-ulotteisessa tapauksessa tarvittavat kopiot = mittakaava.

2-ulotteisessa tapauksessa tarvittavat kopiot = mittakaava^{2}.

3-ulotteisessa tapauksessa tarvittavat kopiot = mittakaava^{3}.

Esimerkkeinä näistä esimerkeistä voidaan päätellä kaava.

Esimerkki

Käytä skaalaus-mitoitus-suhdetta määrittääksesi Sierpinskinin tiivisteen ulottuvuuden.

Esitellään, että määrittelemme alkuperäisen tiivisteen sivun pituudeksi 1. Kuvassa oleva suurempi tiiviste on kaksi kertaa leveämpi ja kaksi kertaa korkeampi, joten se on skaalattu kertoimella 2.

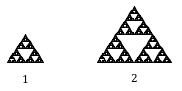
Huomaa, että suuremman tiivisteen rakentamiseen tarvitaan 3 kappaletta alkuperäistä tiivistettä.

Käyttämällä skaalaus-mitoitus-suhdetta C=S^{D}, saadaan yhtälö 3=2^{D}.

Koska 2^{1}=2 ja 2^{2}=4, näemme heti, että D on jossain 1 ja 2 välillä; tiiviste on enemmän kuin yksiulotteinen muoto, mutta olemme ottaneet pois niin paljon pinta-alaa, että sen pinta-ala on nyt alle kaksiulotteinen.

Yhtälön 3=2^{D} ratkaiseminen vaatii logaritmia. Jos olet opiskellut logaritmeja aiemmin, muistat ehkä, miten tämä yhtälö ratkaistaan (jos et, hyppää alla olevaan laatikkoon ja käytä kyseistä kaavaa laskimen log-näppäimellä):

Ota molempien puolien logaritmi.

3={{2}^{D}}

Käytä logaritmien eksponenttiominaisuutta.

\log(3)=\log\left({{2}^{D}}}\right)

Jaa log(2):lla.

\log(3)=D\log\left(2\right)

Tiivisteen ulottuvuus on noin 1,585.

D=\frac{\log\left(3\right)}{\log(2)}\approx1.585

Kokeile

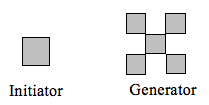
Määritä aloittajalla ja generaattorilla tuotetun fraktaalin fraktaalinen ulottuvuus.

Näytä ratkaisu

Fraktaalin skaalauttaminen 3-kertaiseksi vaatii 5 kopiota alkuperäisestä.

D=\frac{\text{log}\left(5\right)}{\text{log}\left(3\right)}\approx1.465

Seuraavalla videolla esitellään työstetty esimerkki siitä, miten Sierpinskin tiivisteen ulottuvuus voidaan määrittää

.