Osa 14 : Piste- ja Hadamard-tuotto

Vektorit voidaan kertoa aiemmin käsitellyn matriisikerronnan lisäksi kahdella muulla menetelmällä: Pistetuotteella ja Hadamard-tuotteella. Molemmilla menetelmillä saadut tulokset ovat erilaisia.

Samaa riviä ja saraketta vastaavat elementit kerrotaan keskenään ja tuotteet lasketaan yhteen siten, että tulos on skalaari.

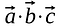
Toisin kuin matriisien kertolaskuissa pistetuoton tulos ei ole toinen vektori tai matriisi, vaan se on skalaari.

Vektoreiden järjestyksellä ei ole väliä pistepotentiaalin kannalta, ainoastaan molempien vektoreiden alkioiden lukumäärän tulee olla sama.

Pistepotentiaalin geometrinen kaava on

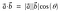
Pistepotentiaalia sanotaan myös sisätuotteeksi tai skalaarituotteeksi.

Vektorin projisointi

Asetetaan, että meillä on kaksi vektoria c ja d, joiden välissä on kulma phi(Ф).

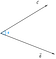
Nyt, vektorin c projektio vektoriin d voidaan esittää seuraavasti

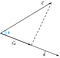
Luvusta voidaan päätellä, että projektio on yhtä suuri kuin vektorin c vaakasuuntainen komponentti vektorin c kulman phi(Ф) suhteen.

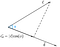
Tätä kutsutaan skalaariprojektioksi.Löytääksemme vektorin c vektoriprojektio vektoriin d meidän on kerrottava skalaariprojektio yksikkövektorilla d.

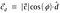
Substituoimalla yksikkövektorin d arvo.

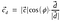
Siten, pistetuotto voitaisiin esittää myös muodossa

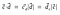
Projektioita käytetään laajalti lineaarialgebrassa ja koneoppimisessa (tukivektorikone(SVM) on koneoppimisalgoritmi, jota käytetään datan luokittelussa).

Hadamard-tuote (elementtikohtainen kertolasku)

Kahden vektorin Hadamard-tuote on hyvin samankaltainen kuin matriisien yhteenlasku, annettujen vektoreiden/matriisien samoja rivejä ja sarakkeita vastaavat elementit kerrotaan keskenään uuden vektorin/matriisin muodostamiseksi.

Se on nimetty ranskalaisen matemaatikon Jacques Hadamardin mukaan.

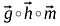
Kerrottavien matriisien/vektoreiden järjestyksen tulee olla sama, ja näin syntyvässä matriisissa on myös sama järjestys.

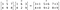
Hadamardin produktiota hyödynnetään kuvienpakkaustekniikoissa, kuten JPEG. Se tunnetaan myös nimellä Schur-tuote saksalaisen matemaatikon Issai Schurin mukaan.

Hadamard-tuotosta käytetään rekursiivisten neuroverkkojen (Recurrent Neural Networks, RNN) LSTM-soluissa (Long Short-Term Memory).