Mitä on analyyttinen geometria?
Mitä on analyyttinen geometria?
Analyyttinen geometria on algebran haara, jota käytetään geometristen objektien mallintamiseen – pisteet, (suorat) viivat ja ympyrät ovat näistä yksinkertaisimpia. Analyyttinen geometria on Descartesin ja Fermat’n suuri keksintö.
Tasojen analyyttisessä geometriassa pisteet määritellään järjestettyinä numeropareina, esimerkiksi (x, y), kun taas suorat puolestaan määritellään lineaarisia yhtälöitä tyydyttävien pisteiden joukoiksi, ks. D. Pedoen tai D. Brannanin ym. erinomaiset ekspositiot.
Yhtälön analyyttisen geometrian kannalta geometriset aksioomat ovat johdettavissa olevia teoreemoja. Esimerkiksi kahdelle eri pisteelle (x1, y1) ja (x2, y2) on olemassa yksi suora ax + by + c = 0, joka kulkee näiden pisteiden kautta. Sen kertoimet a, b, c voidaan löytää (vakiokertoimeen asti) kahden yhtälön lineaarisesta järjestelmästä
| ax1 + by1 + c = 0 ax2 + by2 + c = 0, |
tai suoraan determinanttiyhtälöstä
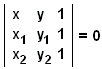 |
Mitään aksiomaattista teoriaa ei kuitenkaan voi paeta käyttämällä määrittelemättömiä osia. Joukkoteoriassa, joka on suuren osan matematiikan ja erityisesti analyyttisen geometrian perustana, joukon perustavin käsite pysyy määrittelemättömänä.
Kolmiulotteisen avaruuden geometriaa mallinnetaan lukukolmioilla (x, y, z) ja kolmiulotteinen lineaarinen 3D-yhtälö ax + by + cz + d = 0 määrittelee tason. Yleisesti ottaen analyyttinen geometria tarjoaa kätevän työkalun työskentelyyn korkeammissa ulottuvuuksissa.
Analyyttisen geometrian puitteissa voidaan mallintaa (ja mallinnetaankin) myös muita kuin euklidisia geometrioita. Esimerkiksi tasoprojektiivisessa geometriassa piste on homogeenisten koordinaattien (x, y, z) kolmikko (x, y, z), joista kaikki eivät ole 0, siten, että
| (tx, ty, tz) = (x, y, z), |
kaikki t ≠ 0, kun taas suoraa kuvaa homogeeninen yhtälö
| ax + bx + cz = 0. |
Analyyttisessä geometriassa kartioleikkaukset määritellään toisen asteen yhtälöillä:
| ax² + bxy + cy² + dx + ey + f = 0. |
Tätä analyyttisen geometrian osaa, joka käsittelee enimmäkseen lineaarisia yhtälöitä, kutsutaan lineaarialgebraksi.
Kartesilainen analyyttinen geometria on geometriaa, jossa akselit x = 0 ja y = 0 ovat kohtisuorassa.
N-parin x = (x1, …, xn) komponentteja kutsutaan sen koordinaateiksi. Kun n = 2 tai n = 3, ensimmäistä koordinaattia kutsutaan abskissaksi ja toista ordinaatiksi.
- D. A. Brannan, M. F. Esplen, J. J. Gray, Geometry, Cambridge University Press, 2002
- D. Pedoe, Geometry: A Comprehensive Course, Dover, 1988
|Yhteys|||Etusivu|||Sisältö||Geometria||Up|
Copyright © 1996-2018 Alexander Bogomolny
Leave a Reply