Lyhyt johdatus differentiaaliseen yksityisyyteen
Aaruran Elamurugaiyan
Privacy can be quantified. Vielä parempi on, että voimme asettaa yksityisyyttä säilyttävät strategiat paremmuusjärjestykseen ja sanoa, mikä niistä on tehokkaampi. Vielä parempaa on, että voimme suunnitella strategioita, jotka ovat vankkoja myös hakkereita vastaan, joilla on aputietoa. Ja aivan kuin tämä ei riittäisi, voimme tehdä kaikki nämä asiat samanaikaisesti. Nämä ja muut ratkaisut löytyvät todennäköisyysteoriasta, jota kutsutaan differentiaaliseksi yksityisyydeksi.
Tässä on konteksti. Hoidamme (tai hallinnoimme) arkaluonteista tietokantaa ja haluaisimme julkaista joitakin tilastoja tästä datasta yleisölle. Meidän on kuitenkin varmistettava, että vastustajan on mahdotonta jäljentää arkaluonteisia tietoja siitä, mitä olemme julkaisseet . Vastustajalla tarkoitetaan tässä tapauksessa osapuolta, jonka tarkoituksena on paljastaa tai saada selville ainakin osa arkaluonteisista tiedoistamme. Differentiaalisella yksityisyydellä voidaan ratkaista ongelmia, jotka syntyvät, kun nämä kolme ainesosaa – arkaluonteiset tiedot, kuraattorit, joiden on julkaistava tilastoja, ja vastustajat, jotka haluavat saada arkaluonteiset tiedot takaisin – ovat läsnä (ks. kuva 1). Tämä käänteinen tietojenkäsittely on eräänlainen yksityisyyden suojan rikkominen.

Mutta kuinka vaikeaa yksityisyyden suojan suojan rikkominen on? Eikö tietojen anonymisointi riittäisi? Jos sinulla on aputietoja muista tietolähteistä, anonymisointi ei riitä. Esimerkiksi vuonna 2007 Netflix julkaisi tietokokonaisuuden käyttäjiensä arvioinneista osana kilpailua, jossa haluttiin nähdä, pystyykö joku päihittämään heidän kollaboratiivisen suodatusalgoritminsa. Tietokokonaisuus ei sisältänyt henkilökohtaisia tunnistetietoja, mutta tutkijat pystyivät silti rikkomaan yksityisyyden suojaa; he saivat takaisin 99 prosenttia kaikista henkilötiedoista, jotka oli poistettu tietokokonaisuudesta . Tässä tapauksessa tutkijat loukkasivat yksityisyyden suojaa käyttämällä IMDB:stä saatuja aputietoja.
Miten kukaan voi puolustautua sellaista vastustajaa vastaan, jolla on tuntematon ja mahdollisesti rajoittamaton apu ulkomaailmasta? Differentiaalinen yksityisyys tarjoaa ratkaisun. Differentiaalisesti yksityiset algoritmit ovat vastustuskykyisiä adaptiivisille hyökkäyksille, jotka käyttävät aputietoa . Nämä algoritmit luottavat satunnaisen kohinan sisällyttämiseen sekaan niin, että kaikesta, mitä vastustaja saa, tulee kohinaa ja epätarkkuutta, jolloin yksityisyyden loukkaaminen on paljon vaikeampaa (jos se ylipäätään on mahdollista).
Noisy Counting
Katsotaanpa yksinkertaista esimerkkiä kohinan lisäämisestä. Oletetaan, että hallinnoimme luottoluokituksia sisältävää tietokantaa (yhteenveto taulukossa 1).
Tässä esimerkissä oletetaan, että vastustaja haluaa tietää niiden ihmisten määrän, joilla on huono luottoluokitus (joka on 3). Tiedot ovat arkaluonteisia, joten emme voi paljastaa perustotuutta. Sen sijaan käytämme algoritmia, joka palauttaa perustotuuden, N = 3, sekä jonkin verran satunnaista kohinaa. Tämä perusajatus (satunnaisen kohinan lisääminen pohjatotuuteen) on avain differentiaaliseen yksityisyyteen. Sanotaan, että valitsemme satunnaisluvun L nollakeskisestä Laplace-jakaumasta, jonka keskihajonta on 2. Palautamme N+L. Selitämme standardipoikkeaman valinnan muutaman kappaleen kuluttua. (Jos et ole kuullut Laplace-jakaumasta, katso kuva 2). Kutsumme tätä algoritmia nimellä ”kohinainen laskenta”.
Jos aiomme ilmoittaa järjettömän, kohinaisen vastauksen, mitä järkeä tässä algoritmissa on? Vastaus on se, että sen avulla voimme löytää tasapainon hyötyjen ja yksityisyyden välillä. Haluamme, että suuri yleisö saa jonkin verran hyötyä tietokannastamme paljastamatta mitään arkaluonteisia tietoja mahdolliselle vastustajalle.
Mitä vastustaja itse asiassa saisi? Vastaukset on raportoitu taulukossa 2.

Ensimmäinen vastauksista, jonka vastustaja saa, on lähellä pohjatodennäköisyyttä mutta ei ole sama. Tässä mielessä vastustajaa on huijattu, hyöty on saatu ja yksityisyys on suojattu. Mutta useiden yritysten jälkeen hän pystyy arvioimaan perustotuuden. Tämä ”estimointi toistuvista kyselyistä” on yksi differentiaalisen yksityisyyden suojan perusrajoituksista. Jos vastustaja voi tehdä tarpeeksi monta kyselyä differentiaalisesti yksityiseen tietokantaan, hän voi silti arvioida arkaluonteiset tiedot. Toisin sanoen yhä useammalla kyselyllä yksityisyys rikkoutuu. Taulukko 2 osoittaa empiirisesti tämän yksityisyyden loukkauksen. Kuten näet, 90 prosentin luottamusväli näistä viidestä kyselystä on kuitenkin melko laaja; arvio ei ole vielä kovin tarkka.
Miten tarkka tuo arvio voi olla? Katso kuviota 3, jossa olemme ajaneet simulaation useita kertoja ja piirtäneet tulokset .

Jokainen pystysuora viiva kuvaa 95 %:n luottamusvälin leveyttä, ja pisteet kuvaavat vastustajan otoksen keskiarvoa. Huomaa, että näissä kuvaajissa on logaritminen vaaka-akseli ja että kohina on poimittu riippumattomista ja identtisesti jakautuneista Laplace-satunnaismuuttujista. Kaiken kaikkiaan keskiarvo on kohinaisempi, kun kyselyitä on vähemmän (koska otoskoko on pieni). Kuten odotettua, luottamusvälit kapenevat, kun vastustaja tekee enemmän kyselyjä (koska otoskoko kasvaa ja kohina on keskimäärin nolla). Pelkästään kuvaajaa tarkastelemalla näemme, että tarvitaan noin 50 kyselyä kunnollisen estimaatin saamiseksi.
Pohditaanpa tuota esimerkkiä. Ensinnäkin lisäämällä satunnaista kohinaa vaikeutimme vastustajan mahdollisuuksia rikkoa yksityisyyden suojaa. Toiseksi käyttämämme salaamisstrategia oli helppo toteuttaa ja ymmärtää. Valitettavasti yhä useammilla kyselyillä vastustaja pystyi lähestymään todellista lukumäärää.
Jos lisäämme lisätyn kohinan varianssia, voimme paremmin puolustaa tietojamme, mutta emme voi yksinkertaisesti lisätä mitä tahansa Laplace-kohinaa funktioon, jonka haluamme salata. Syynä on se, että kohinan määrä, joka meidän on lisättävä, riippuu funktion herkkyydestä, ja jokaisella funktiolla on oma herkkyytensä. Erityisesti laskentafunktion herkkyys on 1. Katsotaanpa, mitä herkkyys tarkoittaa tässä yhteydessä.
Herkkyys ja Laplace-mekanismi
Funktiolle:
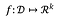
f:n herkkyys on:
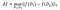
tietoaineistoille D₁, D₂, jotka eroavat toisistaan korkeintaan yhden elementin osalta .
Yllä oleva määritelmä on melko matemaattinen, mutta se ei ole niin huono kuin miltä se näyttää. Karkeasti sanottuna funktion herkkyys on suurin mahdollinen ero, joka yhdellä rivillä voi olla kyseisen funktion tulokseen minkä tahansa tietokokonaisuuden osalta. Esimerkiksi lelutietokannassamme rivien lukumäärän laskemisella on herkkyys 1, koska yhden rivin lisääminen tai poistaminen mistä tahansa tietokannasta muuttaa lukumäärää korkeintaan 1:llä.
Toisena esimerkkinä oletetaan, että ajattelemme ”lukumäärää pyöristettynä 5:n kerrannaiseksi”. Tämän funktion herkkyys on 5, ja voimme osoittaa tämän melko helposti. Jos meillä on kaksi tietokokonaisuutta, joiden koko on 10 ja 11, ne eroavat toisistaan yhdellä rivillä, mutta ”lukumäärät pyöristettynä 5:n kerrannaisiksi” ovat vastaavasti 10 ja 15. Itse asiassa viisi on suurin mahdollinen ero, jonka tämä esimerkkifunktio voi tuottaa. Siksi sen herkkyys on 5.
Herkkyyden laskeminen mielivaltaiselle funktiolle on vaikeaa. Huomattava määrä tutkimustyötä käytetään herkkyyksien arvioimiseen , herkkyysestimaattien parantamiseen ja herkkyyden laskemisen kiertämiseen.
Miten herkkyys liittyy kohinalaskentaan? Meluisa laskentastrategiamme käytti Laplace-mekanismiksi kutsuttua algoritmia, joka puolestaan perustuu sen peittämän funktion herkkyyteen . Algoritmissa 1 on naiivi pseudokooditoteutus Laplace-mekanismista .
Algoritmi 1
Input: F, syöttö X, yksityisyystaso ϵ
tulos: Lasketaan F (X)
Lasketaan F:n herkkyys : S
Poimitaan kohina L Laplace-jakaumasta, jolla on varianssi:
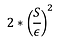
Palauta F(X) + L
Mitä suurempi on herkkyys S, sitä kohinaisempi vastaus on. Laskennan herkkyys on vain 1, joten meidän ei tarvitse lisätä paljon kohinaa yksityisyyden säilyttämiseksi.
Huomaa, että algoritmin 1 Laplace-mekanismi kuluttaa parametrin epsilon. Viittaamme tähän suureeseen mekanismin yksityisyyshäviönä, ja se on osa differentiaalisen yksityisyyden alan keskeisintä määritelmää: epsilon-differentiaalinen yksityisyys. Jos palautamme mieleen aikaisemman esimerkkimme ja käytämme hieman algebraa, voimme nähdä, että meluisalla laskentamekanismillamme on epsilon-differentiaalinen yksityisyys, ja epsilon on 0,707. Virittämällä epsilonin säädämme meluisan laskennan hälyisyyttä. Pienemmän epsilonin valitseminen tuottaa äänettömämpiä tuloksia ja parempia yksityisyystakuita. Vertailukohtana Apple käyttää 2:n epsilonia näppäimistönsä differentiaalisen yksityisyyden automaattisessa korjauksessa .
Määrän epsilon avulla differentiaalinen yksityisyys voi tarjota tarkkoja vertailuja eri strategioiden välillä. Epsilon-differentiaalisen yksityisyyden muodollinen määritelmä on hieman matemaattisesti monimutkaisempi, joten olen tarkoituksella jättänyt sen pois tästä blogikirjoituksesta. Voit lukea siitä lisää Dworkin tutkimuksesta differentiaalisesta yksityisyydestä .
Kuten muistat, kohinaisen laskentaesimerkin epsilon oli 0,707, mikä on melko pieni. Silti yksityisyys rikkoutui 50 kyselyn jälkeen. Miksi? Koska kyselyjen lisääntyessä yksityisyysbudjetti kasvaa, ja siksi yksityisyystakuu huononee.
Tietosuojabudjetti
Yleisesti yksityisyyden suojan menetykset kasautuvat. Kun vastustajalle palautetaan kaksi vastausta, yksityisyyden kokonaishäviö on kaksi kertaa suurempi ja yksityisyystakuu on puolet heikompi. Tämä kumuloituva ominaisuus on seurausta kompositioteoriasta. Pohjimmiltaan jokaisella uudella kyselyllä luovutetaan lisää tietoa arkaluonteisista tiedoista. Näin ollen koostumusteoriassa on pessimistinen näkemys, ja siinä oletetaan pahin mahdollinen skenaario: sama määrä vuotoa tapahtuu jokaisen uuden vastauksen yhteydessä. Vahvoja yksityisyystakuita varten haluamme, että yksityisyyden menetys on pieni. Niinpä esimerkissämme, jossa yksityisyyden menetys on kolmekymmentäviisi (50 kyselyn jälkeen Laplace-kohinanlaskentamekanismillemme), vastaava yksityisyystakuu on hauras.
Miten differentiaalinen yksityisyys toimii, jos yksityisyyden menetys kasvaa niin nopeasti? Varmistaakseen mielekkään yksityisyystakuun tietojen kuraattorit voivat määrätä enimmäisyksityisyyshäviön. Jos kyselyjen määrä ylittää raja-arvon, yksityisyystakuusta tulee liian heikko, ja kuraattori lopettaa kyselyihin vastaamisen. Enimmäisyksityisyyshäviötä kutsutaan yksityisyysbudjetiksi . Voimme ajatella, että jokainen kysely on yksityisyyden suojan ”kustannus”, josta aiheutuu asteittainen yksityisyyden suojan menetys. Strategia, jossa käytetään budjettia, kuluja ja menetyksiä, tunnetaan osuvasti nimellä privacy accounting .
Privacy accounting on tehokas strategia, jolla voidaan laskea yksityisyyden menetys useiden kyselyjen jälkeen, mutta siihen voidaan silti sisällyttää kompositioteoreema. Kuten aiemmin todettiin, koostumusteoriassa oletetaan pahin mahdollinen skenaario. Toisin sanoen parempia vaihtoehtoja on olemassa.
Syväoppiminen
Syväoppiminen on koneoppimisen osa-alue, joka liittyy syvien neuroverkkojen (DNN) kouluttamiseen tuntemattomien funktioiden arvioimiseksi . (Korkealla tasolla DNN on sarja affiinisia ja epälineaarisia muunnoksia, jotka kuvaavat jonkin n-ulotteisen avaruuden m-ulotteiseen avaruuteen.) Sen sovellukset ovat laajalle levinneitä, eikä niitä tarvitse toistaa tässä. Tutkitaan, miten syvä neuroverkko koulutetaan yksityisesti.
Syviä neuroverkkoja koulutetaan tyypillisesti käyttämällä stokastisen gradienttilaskeutumisen (SGD) muunnosta. Abadi et al. keksivät tästä suositusta algoritmista yksityisyyttä säilyttävän version, jota kutsutaan yleisesti ”yksityiseksi SGD:ksi” (tai PSGD:ksi). Kuva 4 havainnollistaa heidän uuden tekniikkansa tehoa. Abadi et al. keksivät uuden lähestymistavan: momenttitilinpitäjän. Momenttien kirjanpitäjän perusajatuksena on kerätä yksityisyysmenot muodostamalla yksityisyyden menetys satunnaismuuttujaksi ja käyttämällä sen momentteja tuottavia funktioita kyseisen muuttujan jakauman parempaan ymmärtämiseen (tästä nimi) . Täydelliset tekniset yksityiskohdat eivät kuulu esittelevän blogikirjoituksen piiriin, mutta suosittelemme lukemaan alkuperäisen artikkelin saadaksesi lisätietoja.

Loppuajatuksia
Olemme tarkastelleet differentiaalisen yksityisyyden teoriaa ja nähneet, miten sitä voidaan käyttää yksityisyyden kvantifiointiin. Tämän postauksen esimerkit osoittavat, miten perusajatuksia voidaan soveltaa, sekä sovelluksen ja teorian välisen yhteyden. On tärkeää muistaa, että yksityisyystakeet heikkenevät toistuvan käytön myötä, joten kannattaa miettiä, miten tätä voidaan lieventää, olipa kyse sitten yksityisyysbudjetoinnista tai muista strategioista. Voit tutkia heikkenemistä klikkaamalla tätä lausetta ja toistamalla kokeilumme. On vielä monia kysymyksiä, joihin ei ole vastattu tässä, ja runsaasti kirjallisuutta tutkittavaksi – katso alla olevat viitteet. Kannustamme sinua lukemaan lisää.
Cynthia Dwork. Differentiaalinen yksityisyys: A survey of results. International Conference on Theory and Applications of Models of Computation, 2008.
Wikipedia Contributors. Laplace-jakauma, heinäkuu 2018.
Aaruran Elamurugaiyan. Plots demonstrating standard error of differentially private responses over number of queries., August 2018.
Benjamin I. P. Rubinstein and Francesco Alda. Kivuton satunnainen differentiaalinen yksityisyys herkkyysnäytteenotolla. In 34th International Conference on Machine Learning (ICML’2017) , 2017.
Cynthia Dwork ja Aaron Roth. Differentiaalisen yksityisyyden algoritmiset perusteet . Now Publ., 2014.
Martin Abadi, Andy Chu, Ian Goodfellow, H. Brendan Mcmahan, Ilya Mironov, Kunal Talwar ja Li Zhang. Deep learning with differential privacy. Proceedings of the 2016 ACM SIGSAC Conference on Computer and Communications Security – CCS16 , 2016.
Frank D. McSherry. Yksityisyyden suojaan integroidut kyselyt: Laajennettava alusta yksityisyydensuojan säilyttävään data-analyysiin. In Proceedings of the 2009 ACM SIGMOD International Conference on Management of Data , SIGMOD ’09, pages 19-30, New York, NY, USA, 2009. ACM.
Wikipedia Osallistujat. Deep Learning, elokuu 2018.
Leave a Reply