Introduction to Deconvolution

Dekonvoluutio on laskentaintensiivinen kuvankäsittelytekniikka, jota käytetään yhä useammin mikroskoopilla otettujen digitaalisten kuvien kontrastin ja resoluution parantamiseen. Perustana on joukko menetelmiä, joiden tarkoituksena on poistaa tai kumota mikroskooppikuvissa esiintyvä epätarkkuus, joka johtuu objektiivin rajallisesta aukosta.

Lähes mikä tahansa digitaalisella fluoresenssimikroskoopilla otettu kuva voidaan dekonvolvoida, ja kehitteillä on useita uusia sovelluksia, joissa dekonvoluutiotekniikoita sovelletaan läpikuultavassa valossa otettaviin kuviin, jotka on kerätty erilaisilla kontrastinparannusstrategioilla. Parhaiten dekonvoluutiolla parannettavaksi soveltuvia kohteita ovat optisista leikkaussarjoista rakennetut kolmiulotteiset montaasit.

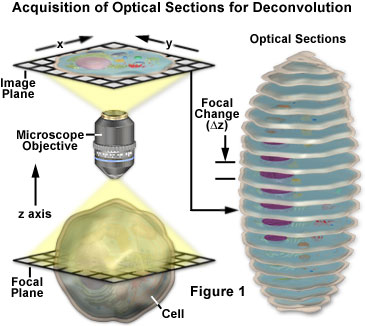
Kuvassa 1 on esitetty kaavamaisesti z-sarjan kuvien hankkimiseen dekonvoluutioanalyysia varten liittyvät peruskäsitteet. Näytteestä tallennetaan sarja kuvia, joista jokainen on siirretty hieman toisistaan z-akselia pitkin. Tämä tarkennustason muutos johtaa hieman erilaiseen kuvaan, jossa on hienovaraisia muutoksia, jotka johtuvat nykyisen z-tason ylä- ja alapuolelta tulevasta epätarkasta valosta. Dekonvoluutioanalyysin aikana koko z-sarja analysoidaan selkeämmän, korkeamman resoluution datasarjan luomiseksi, jota ei vääristä tarkennuksen ulkopuolinen fluoresenssi.

Konvoluutiota ehdotetaan usein hyväksi vaihtoehdoksi konfokaalimikroskoopille, sillä molemmilla tekniikoilla pyritään minimoimaan tarkennuksen ulkopuolisen fluoresenssin vaikutus lopulliseen kuvaan. Tämä ei pidä täysin paikkansa, koska konfokaalimikroskoopin pinhole-aukolla otetut kuvat hyötyvät dekonvoluutiokäsittelystä. Konfokaalimikroskopiassa estetään epätarkennetun valon havaitseminen asettamalla objektiivin ja ilmaisimen väliin reikäaukko, jonka läpi vain tarkennetut valonsäteet pääsevät. Laajakenttämikroskoopit sen sijaan päästävät tarkentumattoman valon suoraan ilmaisimelle. Tämän jälkeen tuloksena saatuihin kuviin sovelletaan dekonvoluutiota, jolla joko vähennetään epätarkka valo tai kohdistetaan se takaisin sen lähteeseen. Konfokaalimikroskopia soveltuu erityisen hyvin paksujen näytteiden, kuten alkioiden tai tussujen, tutkimiseen, kun taas laajakenttädekonvoluution käsittely on osoittautunut tehokkaaksi välineeksi kuvattaessa näytteitä, jotka vaativat erittäin alhaisia valotasoja. Näitä työkaluja voidaan jopa yhdistää konfokaalimikroskoopilla otettujen kuvien kohinan vähentämiseksi. Suurin osa kirjallisuudessa raportoiduista dekonvoluutiokokeista koskee kuitenkin kuvia, jotka on tallennettu tavallisella laajakenttäfluoresenssimikroskoopilla.

Kuvan heikkenemisen lähteet

Kuvan heikkeneminen jaetaan neljään itsenäiseen lähteeseen: kohinaan, sirontaan, häikäisyyn ja epätarkkuuteen. Kuvassa 2 esitetään esimerkkejä kunkin näistä visuaalisesta vaikutuksesta samaan kuvaan.

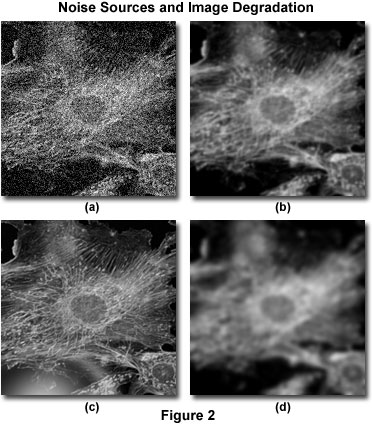
Kohinaa voidaan kuvata kuvan yksityiskohtien näennäisen satunnaiseksi sekoittumiseksi, joka (vakavimmassa muodossaan) näyttää valkoiselta kohinalta tai suolaista kohinaa sisältävältä kohinalta, joka on samankaltaista kuin se, mikä nähdään yleisradiolähetyksissä huonon kuuluvuuden aikana (kuva 2(a)). Tämäntyyppistä kohinaa kutsutaan ”lähes satunnaiseksi”, koska sen tilastollinen jakauma voidaan ennustaa, jos lähteen mekaniikka tunnetaan. Digitaalisessa mikroskopiassa pääasiallinen kohinan lähde on joko itse signaali (jota usein kutsutaan fotonilaukaisukohinaksi) tai digitaalinen kuvantamisjärjestelmä. Molempien kohinanlähteiden mekaniikka tunnetaan, joten kohinan tilastollinen jakauma tunnetaan. Signaalista riippuvaista kohinaa voidaan luonnehtia Poisson-jakaumalla, kun taas kuvantamisjärjestelmästä aiheutuva kohina noudattaa usein Gaussin jakaumaa. Koska digitaalisissa kuvissa esiintyvän yleisen kohinan lähde ja jakauma tunnetaan niin hyvin, se voidaan helposti poistaa soveltuvilla kuvasuodattimilla, jotka yleensä sisältyvät useimpiin dekonvoluutio-ohjelmistopaketteihin valinnaisena esikäsittelyrutiinina.

Sirontaan viitataan yleensä valon satunnaisena häiriönä, joka aiheutuu taitekertoimen muutoksista näytteessä. Sironnan nettovaikutus on kuvan yksityiskohtien todella satunnainen sekoittuminen, kuten kuvassa 2(b) on esitetty. Vaikka täysin tyydyttävää menetelmää sironnan ennustamiseksi tietyssä näytteessä ei ole kehitetty, on osoitettu, että sironnan aste riippuu suuresti näytteen paksuudesta sekä näytteen ja ympäröivien upotusmateriaalien optisista ominaisuuksista. Sironta kasvaa sekä näytteen paksuuden että näytteen sisäisten komponenttien taitekertoimen heterogeenisuuden myötä.

Häikäisy on sironnan tavoin valon satunnainen häiriö, mutta se tapahtuu mikroskoopin optisissa elementeissä (linssit, suodattimet, prismat jne.) eikä näytteessä. Nykyaikaisessa mikroskoopissa esiintyvää häikäisyä on vähennetty minimiin käyttämällä heijastusta vähentäviä pinnoitteita sisältäviä linssejä ja suodattimia sekä parantamalla linssien muotoilutekniikoita, optisia sementtejä ja lasin koostumusta. Kuva 2(c) havainnollistaa hallitsemattoman häikäisyn vaikutusta.

Hämärtymistä kuvataan valon ei-sattumanvaraisella leviämisellä, joka tapahtuu kulkiessa kuvantamisjärjestelmän optisen reitin läpi (kuva 2(d)). Merkittävin epätarkkuuden lähde on diffraktio, ja kuvaa, jonka erotuskykyä rajoittaa vain epätarkkuus, pidetään diffraktiorajoitteisena. Tämä on minkä tahansa kuvantamisjärjestelmän luontainen raja, ja se on ratkaiseva tekijä arvioitaessa optisen järjestelmän erottelukyvyn rajaa. Onneksi on saatavilla kehittyneitä optisen mikroskoopin epätarkkuuden malleja, joita voidaan käyttää tarkennuksen ulkopuolisten fotonien lähteen määrittämiseen. Tämä on dekonvoluution perusta. Koska epätarkkuuden teoreettinen malli on olennaisen tärkeä dekonvoluutiossa, sitä käsitellään paljon yksityiskohtaisemmin tämän jakson muissa osissa. On kuitenkin korostettava, että kaikki kuvantamisjärjestelmät tuottavat epätarkkuutta riippumatta muista näytteen tai siihen liittyvän instrumenttielektroniikan aiheuttamista kuvan heikkenemismuodoista. Juuri tämä optisen epätarkkuuden riippumattomuus muunlaisesta heikkenemisestä mahdollistaa epätarkkuuden poistamisen dekonvoluutiotekniikoilla.

Valon ja aineen vuorovaikutus on sironnan, häikäisyn ja epätarkkuuden ensisijainen fysikaalinen alkuperä. Tietyn materiaalin (olipa se sitten lasia, vettä tai proteiinia) molekyylien koostumus ja sijoittelu antavat kuitenkin kullekin materiaalille omat erityiset optiset ominaisuutensa. Dekonvoluution kannalta hajonnan, häikäisyn ja epätarkkuuden erottaa toisistaan niiden esiintymispaikka ja mahdollisuus luoda matemaattinen malli näille ilmiöille. Koska sironta on paikallinen, epäsäännöllinen ilmiö, joka esiintyy näytteessä, sen mallintaminen on osoittautunut vaikeaksi. Sitä vastoin, koska epätarkkuus on mikroskoopin optisen järjestelmän (pääasiassa objektiivin) funktio, se voidaan mallintaa suhteellisen yksinkertaisesti. Tällaisen mallin avulla on mahdollista kääntää epätarkkuusprosessi matemaattisesti, ja dekonvoluutio käyttää tätä mallia epätarkkuuden kumoamiseen tai poistamiseen.

Pistehajontafunktio

Teoreettisen optiikan piirissä kehittynyt epätarkkuuden malli perustuu kolmiulotteisen pistehajontafunktion (point spread function, PSF) käsitteeseen. Tällä käsitteellä on perustavanlaatuinen merkitys dekonvoluutiossa, ja se on ymmärrettävä selvästi, jotta vältetään kuvausartefakteja. Pistehajontafunktio perustuu äärettömän pieneen pistemäiseen valonlähteeseen, joka on peräisin näytteen (objektin) tilasta. Koska mikroskoopin kuvantamisjärjestelmä kerää vain murto-osan tämän pisteen lähettämästä valosta, se ei voi keskittää valoa täydelliseksi kolmiulotteiseksi kuvaksi pisteestä. Sen sijaan piste näkyy laajentuneena ja levittyneenä kolmiulotteiseksi diffraktiokuvioksi. Siten pisteen leviämisfunktio määritellään muodollisesti ihanteellisen pistemäisen valonlähteen tuottamaksi kolmiulotteiseksi diffraktiokuvioksi.

Hyödynnettävästä kuvantamismuodosta (laajakenttä-, konfokaali-, läpäisevän valon kuvausmuodosta) riippuen pisteen leviämisfunktio on muodoltaan ja ääriviivoiltaan erilainen ja ainutlaatuinen. Laajakenttämikroskoopissa fluoresenssimikroskoopissa pisteen leviämisfunktion muoto muistuttaa pitkulaista ”jalkapalloa”, jota ympäröi levenevien renkaiden soihtu. Pistehajontafunktion kuvaamiseksi kolmiulotteisesti käytetään yleensä kolmiakselista koordinaattijärjestelmää (x, y ja z), jossa x ja y ovat yhdensuuntaiset näytteen polttotasoon nähden ja z on yhdensuuntainen mikroskoopin optisen akselin kanssa. Tällöin pisteen leviämisfunktio näkyy x-y-tasossa keskittyneinä renkaina ja muistuttaa tiimalasia x-z- ja y-z-tasoissa (kuten kuvassa 3 on esitetty). Laajakenttäisen pisteen leviämisfunktion keskipisteen läpi kulkeva x-y-viilto paljastaa joukon samankeskisiä renkaita: niin sanottu Airyn kiekko, johon viitataan yleisesti klassista optista mikroskopiaa käsittelevissä teksteissä.

Kahdessa x-z-projektiossa pisteen leviämisfunktioista, joissa näkyy eriasteista sfääristä aberraatiota, on esitetty kuva 3. Optinen akseli on kuvan pystyakselin suuntainen. Vasemmalla olevassa pisteen leviämisfunktiossa on minimaalinen sfäärinen aberraatio, kun taas oikealla olevassa pisteen leviämisfunktiossa on huomattavaa aberraatiota. Huomaa, että oikeanpuoleisessa kuvassa aksiaalinen epäsymmetria ja keskussolmun leveneminen optisen akselin suuntaisesti johtaa aksiaalisen resoluution heikkenemiseen ja signaalin sumentumiseen. Teoriassa pisteiden leviämisfunktion koko on ääretön, ja valon yhteenlaskettu kokonaisintensiteetti kaukana fokuksesta olevissa tasoissa on yhtä suuri kuin yhteenlaskettu intensiteetti fokuksessa. Valon voimakkuus kuitenkin laskee nopeasti ja muuttuu lopulta erottamattomaksi kohinasta. Suurella numeerisella aukolla (1,40) varustetulla öljyimmersio-objektiivilla rekisteröidyssä harhattomassa pisteen leviämisfunktiossa valo, joka täyttää 0,2 neliömikrometriä tarkennustasossa, leviää 90-kertaisesti samalle alueelle yhden mikrometrin etäisyydelle tarkennuksen ylä- ja alapuolella. Näyte, jota käytettiin näiden pisteen leviämisfunktion kuvien tallentamiseen, oli halkaisijaltaan 0,1 mikrometrin läpimittainen fluoresoiva helmi, joka oli kiinnitetty glyseroliin (taitekerroin yhtä suuri kuin 1,47), ja immersioöljyt, joiden taitekertoimet on merkitty kuvassa.

Tärkeä näkökohta on se, miten pisteen leviämisfunktio vaikuttaa kuvanmuodostukseen mikroskoopissa. Kuvanmuodostuksen teoreettisessa mallissa käsitellään pisteen leviämisfunktiota kuvan perusyksikkönä. Toisin sanoen pisteen hajontafunktio on kuvalle se, mikä tiili on talolle. Parasta, mitä kuva voi koskaan olla, on pistehajontafunktioiden muodostama kokonaisuus, eikä suurennuksen lisääminen muuta tätä tosiasiaa. Kuten eräässä tunnetussa teoreettisen optiikan oppikirjassa (Born ja Wolf: Principles of Optics) selitetään: ”On mahdotonta tuoda esiin yksityiskohtia, joita ei ole primaarikuvassa, lisäämällä okulaarin voimakkuutta, sillä jokainen primaarikuvan elementti on pieni diffraktiokuvio, ja varsinainen kuva, sellaisena kuin se nähdään okulaarista, on vain näiden kuvioiden suurennettujen kuvien kokonaisuus.”

Esimerkkinä voidaan ajatella populaatiota aliresoluutioisia fluoresoivia helmiäisjoukkoja, jotka on sijoitettu peitinliuskan ja objektilasin väliin. Tarkennettu kuva tästä näytteestä paljastaa pisteiden pilven, joka on itse asiassa kiekko, jota ympäröi pieni joukko renkaita (itse asiassa Airyn kiekko; ks. kuva 4(a)). Jos näytettä siirretään hieman pois tarkennuksesta, kunkin pisteen kohdalla tarkennetussa kuvassa näkyy suurempi joukko samankeskisiä renkaita (kuva 4(b)). Kun tästä näytteestä kerätään kolmiulotteinen kuva, jokaisesta helmestä tallennetaan täydellinen pisteen leviämisfunktio. Pistehajontafunktio kuvaa, mitä kullekin pistemäiselle valonlähteelle tapahtuu sen jälkeen, kun se on kulkenut kuvantamisjärjestelmän läpi.

Äsken kuvattu sumentumisprosessi mallinnetaan matemaattisesti konvoluutioksi. Konvoluutio-operaatio kuvaa pistehajontafunktion soveltamista näytteen jokaiseen pisteeseen: objektin jokaisesta pisteestä lähtevä valo konvoluoidaan pistehajontafunktion kanssa lopullisen kuvan tuottamiseksi. Valitettavasti tämä konvoluutio aiheuttaa sen, että näytteen pisteistä tulee kuvaan epäselviä alueita. Kuvan jokaisen pisteen kirkkaus on konvoluutio-operaation avulla lineaarisesti verrannollinen näytteen jokaisen pisteen fluoresenssiin. Koska pisteiden leviämisfunktio on kolmiulotteinen, pisteiden leviämisfunktion aiheuttama epätarkkuus on luonnostaan kolmiulotteinen ilmiö. Mistä tahansa polttotasosta saatu kuva sisältää kyseisessä tasossa sijaitsevista pisteistä peräisin olevaa sumentunutta valoa sekoittuneena muista polttotasoista peräisin olevista pisteistä peräisin olevaan sumentuneeseen valoon.

Tilanne voidaan tiivistää ajatuksella, että kuva muodostuu näytteen konvoluutiosta pistehajontafunktion kanssa. Dekonvoluutio kääntää tämän prosessin päinvastaiseksi ja yrittää rekonstruoida näytteen epäselvästä kuvasta.

Pistehajontafunktiossa esiintyvät poikkeamat

Pistehajontafunktio voidaan määritellä joko teoreettisesti käyttämällä matemaattista diffraktiomallia tai empiirisesti hankkimalla kolmiulotteinen kuva fluoresoivasta helmestä (ks. kuva 3). Teoreettisella pisteen leviämisfunktiolla on yleensä aksiaalinen ja radiaalinen symmetria. Pistehajontafunktio on symmetrinen x-y-tason ylä- ja alapuolella (aksiaalinen symmetria) ja z-akselin suhteen (radiaalinen symmetria). Empiirinen pisteen leviämisfunktio voi poiketa merkittävästi täydellisestä symmetriasta (kuten kuvassa 3 on esitetty). Tämä poikkeama, jota kutsutaan yleisemmin aberraatioksi, johtuu epäsäännöllisyyksistä tai vääristä linjauksista missä tahansa kuvantamisjärjestelmän optisen järjestelmän komponentissa, erityisesti objektiivissa, mutta sitä voi esiintyä myös muissa komponenteissa, kuten peileissä, säteenjakajissa, putkilinsseissä, suodattimissa, kalvoissa ja aukoissa. Mitä laadukkaampia optiset komponentit ovat ja mitä paremmin mikroskooppi on kohdistettu, sitä lähempänä empiirinen pistehajontafunktio on ihanteellista symmetristä muotoa. Sekä konfokaali- että dekonvoluutiomikroskopia ovat riippuvaisia siitä, että pisteen hajontafunktio on mahdollisimman lähellä ideaalista tapausta.

Yleisin optisessa mikroskopiassa esiintyvä aberraatio, jonka kaikki kokeneet ja ammattimaiset mikroskoopikot tuntevat hyvin, on sfäärinen aberraatio. Tämän aberraation ilmenemismuoto on pisteiden leviämisfunktion muodon aksiaalinen epäsymmetria ja vastaava koon kasvu erityisesti z-akselin suuntaisesti (kuva 3). Tuloksena on huomattava resoluution ja signaalin voimakkuuden heikkeneminen. Käytännössä sfäärisen aberraation tyypillinen lähde on objektiivin etulinssin upotusmediumin ja näytettä sisältävän kiinnitysmediumin taitekertoimien epäsuhta. Tämän aberraation minimoimisen tärkeyttä olisi korostettava valtavasti. Vaikka dekonvoluutio voi osittain palauttaa menetetyn resoluution, mikään määrä kuvankäsittelyä ei voi palauttaa menetettyä signaalia.